躺平or內卷，或許這條數學定律能幫你選擇最優解_風聞

在大自然中，動物為了攝食或者繁衍後代，往往面臨着收益與體力的抉擇。比如大山雀在灌木叢中捕食，開始它會很容易找到毛毛蟲，一段時間後則越來越難以找到，甚至最後找到食物卻不足以彌補尋覓過程的體力消耗。那麼，什麼時候應該離開這片區域，另尋他路？人們驚奇地發現，動物往往會本能地選擇最優解決方式，即將所得收益最大化。而在數學上，這就是邊際價值定理所展現的。

撰文 | James V. Stone（英國謝菲爾德大學名譽副教授）

翻譯 | 施昊

懂得何時適可而止是我們人生中的一大難題。當面對收益遞減時，選擇堅持，還是放棄當下，以期將來獲得更豐厚的回報，這樣的困境比比皆是。對於每一座金礦來説，都會到達一個節點——繼續開採所得到的黃金不能抵上所付出的成本，一旦這個時間點到了，就是時候放棄開採，開始尋找新的金礦了。

相似的，對於在灌木叢中以毛毛蟲為食的鳥來説，當它們獲得的卡路里不足以繼續尋找更多毛毛蟲的時候，也是時候放棄在這裏捕食，應轉而去另一片灌木叢。同樣，對於蜜蜂而言，收集花粉的重量與其所需能量不相匹配的時候，此時應停止收集，該飛回蜂巢了。

幸運的是，數學上有個解決方案——邊際價值定理（Marginal value theorem，1976年由美國生態學家Eric Charnov提出）。邊際效益理論明確指出了何時放棄以獲得最大的回報。更重要的是，從最初的最佳覓食理論到大腦如何處理信息，邊際價值定理已經有了很廣泛的應用。本質上，無論你所付出或收穫是什麼，邊際價值理論提供了一種一般的策略，即將每份付出所得最大化。

捕食中的瓢蟲

瓢蟲和蚜蟲丨圖片來源：Greyson Orlando

瓢蟲以蚜蟲為食，但是看瓢蟲吃蚜蟲就像看人類吃龍蝦，因為蚜蟲的外骨骼對於瓢蟲來説就像龍蝦的外殼對於人類一樣，難以直接穿透進食。一開始吃完最多汁的部分之後，往往需要越來越多的努力來獲取越來越少的食物。人類面臨這個難題往往懂得適可而止，轉而享用別的美食。同樣的，當瓢蟲面臨這樣的問題，也知道什麼時候放棄轉而去找另一隻蚜蟲。

如果瓢蟲過早的放棄眼前這隻，它將會浪費掉容易獲得的一部分食物。相反，如果過遲放棄，大費周章卻得到的越來越少，而這三三兩兩本可以從另一隻蚜蟲身上輕鬆獲得。顯然，有一個既不過早也不太晚、“恰到好處”的時間來放棄。為了弄清楚這個“恰到好處”的時間點何時到來，我們需要更加詳細地瞭解瓢蟲的進食行為。

蚜蟲類似於龍蝦的解剖學性質意味着，如果讓一隻瓢蟲只吃一隻蚜蟲，那麼累計進食的重量會隨着餵食時間t的增加而增加，如下圖所示。（這個數據來自與R. M. Cook 和B. J. Cockrell 發表於1978年一篇經典的關於覓食理論的文章[1]，這篇文章啓發了我們舉了瓢蟲的示例。）

黑色的點表示t分鐘時刻瓢蟲進食的食物質量，黑色曲線表示擬合的收益曲線E(t)。

圖中黑色的曲線是收益函數E(t)，曲線的斜率是即時收益率r(t)。紅色虛線表示移動平均收益率R(t)。這個圖反映了瓢蟲過早放棄蚜蟲的情況。

在上圖中，進食的時間為t=10min，紅色的虛線的斜率比較小；如果瓢蟲延遲放棄進食，斜率將會變大，它放棄得太早了。如果進食時間超過10分鐘，移動平均收益率R(t)將會變大。

瓢蟲過遲放棄蚜蟲

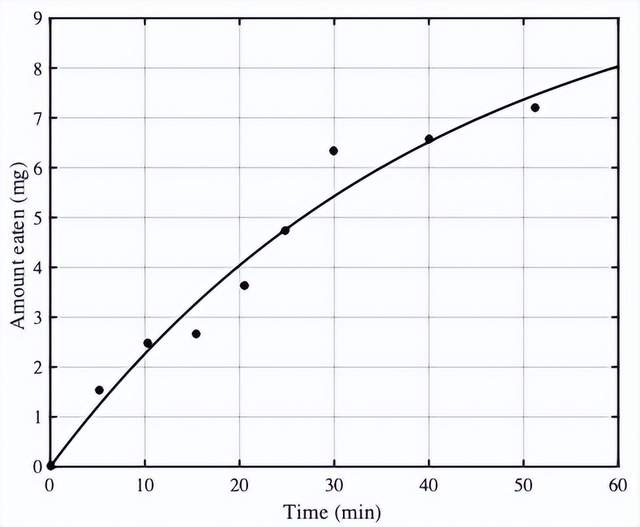
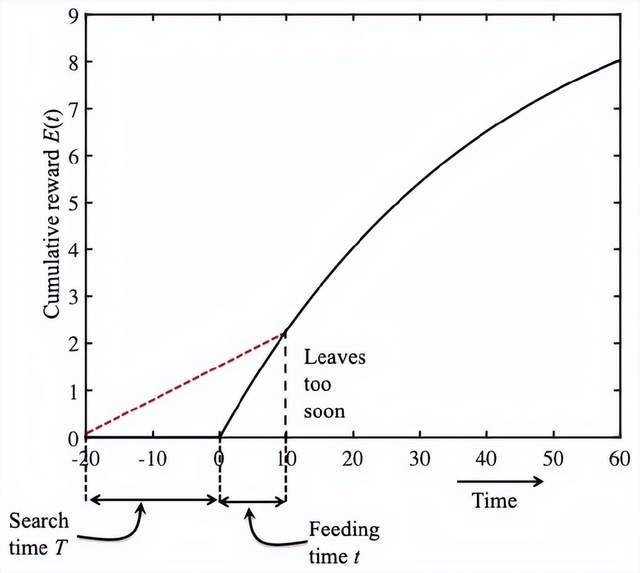
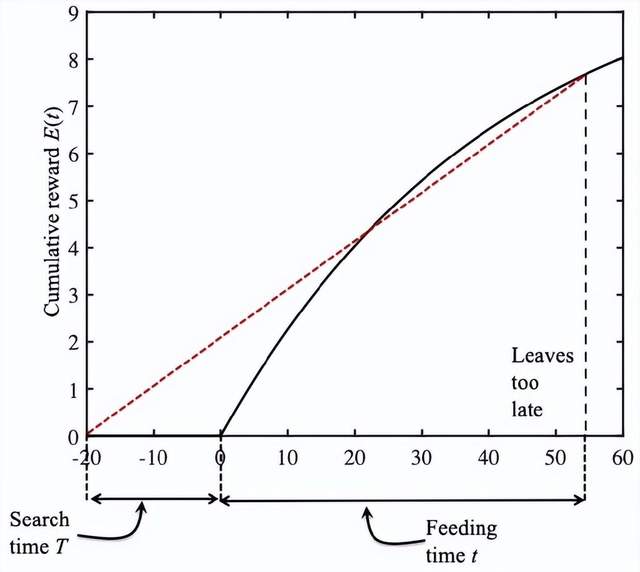
同樣地，如上圖所示，進食的時間為t=55min，紅色虛線的斜率也比較小，如果瓢蟲提前放棄進食，斜率將會變大，它離開得太遲了。如果進食小於55分鐘，移動平均收益率R(t)將會變大。

瓢蟲在恰好的時間放棄進食。

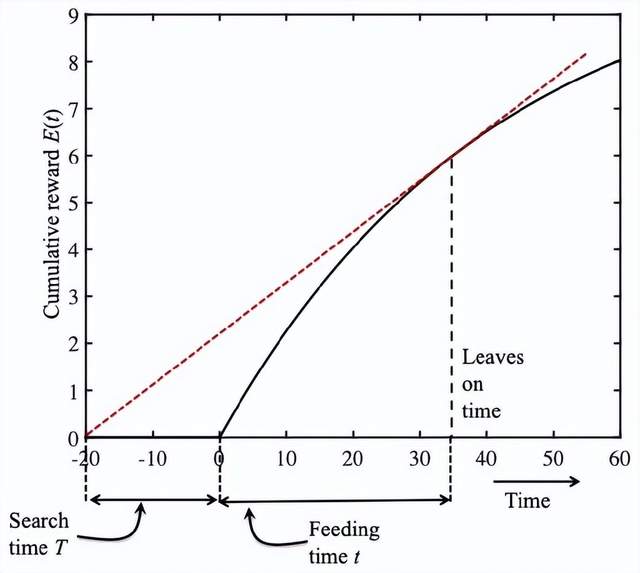
最後，進食時間t=35min產生了一個可能最大的斜率。這是最優的進食時間，如果此時放棄進食，移動平均收益率R(t)將會最大。

注意到“恰到好處”的進食時間發生在收益曲線的斜率r(t)等於紅色虛線的斜率，也就是移動平均收益率R(t)的時刻。換句話説，恰到好處的進食時間發生在即時收益率等於移動平均收益率的時候：r(t)=R(t)。

可以用幾何驗證，即時收益率r(t)在下圖用紅色的虛線表示，移動平均收益率R(t)用黑色的實線表示。

紅色虛線表明即時收益率，黑色實線表示移動平均收益率

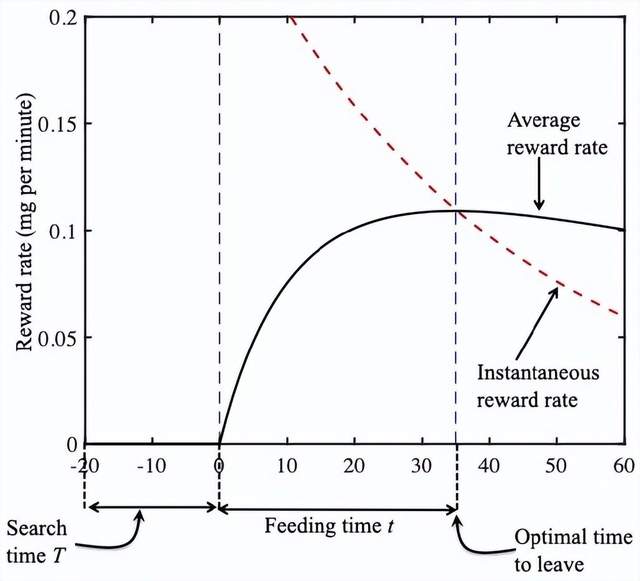
正如我們預料那樣，這兩條曲線在“恰到好處”的時間相交（也就是r(t)=R(t)）。從這種幾何角度的分析有效證明了邊際價值定理，也就是最佳的退出時間是當即時收益率等於移動平均收益率的時候，也就是當r(t)=R(t)。

數學證明如下：

在下面三個相當弱（温和）的條件下，邊際價值定理是成立的：

1. 固定成本T大於0；

2. 收益函數E(t)隨着時間t增加而增加；

我們希望證明當R(t)最大時候，即時收益率r(t)等於平均收益率R(t)。為此，我們需要找到當R(t)最大時，r(t)的值。為了找到最大的平均收益率，我們要用到（平均收益率）在它的斜率為0處最大這個事實。

平均收益率被定義為：

以及它的導數是

根據定義，

是即時收益率，以及

把等式（3）和（4）代入到等式（2）中，可以得到

又因為

是平均收益率，所以公式（5）變成了

在最大值處，令上式等於0，

最後在等式兩邊同時乘上T+t，移項得

這就證明了當即時收益率等於平均收益率得時候，平均收益率將會達到最大。

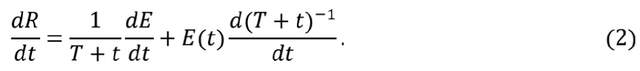
瓢蟲懂得邊際價值定理

上述的分析假設了一個恆定不變的搜索時間T。但是，對邊際價值定理一個妥當的檢驗應涉及到可變的搜索時間。本質上來講，較長的搜索時間表明食物比較稀缺，因此相應地增加進食每隻蚜蟲的時間是有道理的。換句話説，在一隻蚜蟲身上花費的進食時間應該隨着尋找到這隻蚜蟲所花費的時間增加而增加。然而，相比於這個正確但是模糊的結論，邊際價值理論精準地預測了進食時間該如何隨着搜索時間增加而增加，如下圖所示。（再次使用了建立在Cook和Cockrell 1978年實驗數據的收益函數）。

如果用40分鐘找到一隻蚜蟲，瓢蟲將會花費50分鐘來進食這隻蚜蟲（紅色的虛線）；如果用10分鐘找到了一隻蚜蟲，瓢蟲將會花費28分鐘來進食這隻蚜蟲（藍色虛線）。

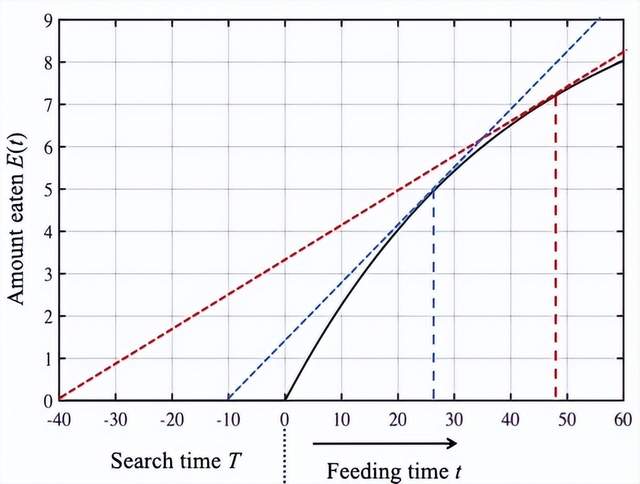
從上圖中我們可以看出，邊際價值定理預測以蚜蟲為食的時間會隨着尋找蚜蟲的時間增加而增加。如果找到一隻蚜蟲需要40分鐘，那麼瓢蟲應該花費大約50分鐘來進食（上圖中的紅色虛線）。如果找到一隻蚜蟲需要10分鐘，那麼瓢蟲應該只花費大約28分鐘來進食（藍色虛線）。

問題是，瓢蟲會按照邊際價值定理預測的時間放棄進食蚜蟲嗎？為了回答這個問題，Cook和Cockrell 將蚜蟲隨機散放在一個托盤裏，然後測量瓢蟲幼蟲找到每隻蚜蟲所花費的時間T以及進食每隻蚜蟲所花費的時間t。（Cook和Cockrell 使用了瓢蟲幼蟲，不過這個並不是很重要。）

瓢蟲幼蟲平均進食時間如何隨着找到一隻蚜蟲的時間變化：點表示實驗中觀察值，黑色的線表示由邊際價值理論預測的進食時間。

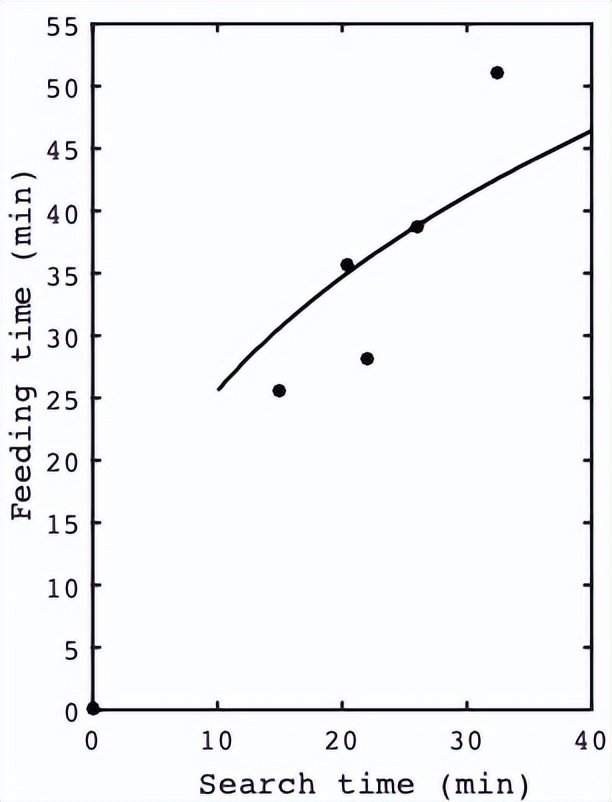
上圖顯示了Cook 和 Cockrell 觀察到的瓢蟲幼蟲的平均攝食時間如何隨着搜索時間變化的：點代表着他們在實驗中觀察到的結果，黑色的曲線代表着邊際價值定理預測的進食時間。經過多次實驗，蚜蟲的數量漸漸減少，使得搜索新的蚜蟲的時間相應地變長。如預測的一樣，隨着搜索的時間增加（蚜蟲的密度降低），每隻蚜蟲平均被食用的時間也會增加。更重要的是，這樣隨着搜索時間增加而進食時間增加的方式，在某種程度上和邊際價值定理預測的一致，正如上圖所示。

在這個特定的例子中，數據和理論之間的擬合不是那麼令人印象深刻，這可能因為移動平均收益函數R(t)沒有一個尖峯，因此提前一點或者推遲一點放棄進食所損失的收益相對來説比較小。相反，如果收益函數上升的十分陡峭，那麼移動平均收益率曲線會有一個更高的鋒，那麼實驗的數據和邊際價值定理預測值可能會更加匹配。

動物懂得何時適可而止

瓢蟲捕食蚜蟲的過程，只是動物在合適的時間放棄進食以達到最大效益的眾多例子中的一個。同樣的道理也適用於獲取寶貴資源所需高昂成本的情況下。

大山雀的偉大智慧

大山雀捕食丨圖片來源：Rosember

假設一隻大山雀花費了一些時間尋找到有大量毛毛蟲的灌木叢。找到灌木叢後，大山雀開始每分鐘可以吃到的大量的毛毛蟲，但是過了一會兒，可以找到的毛毛蟲數量下降了，因此每分鐘可以吃到的毛毛蟲數量也下降了。鑑於邊際收益的遞減，大山雀該何時放棄這片灌木叢而選擇去尋找新的灌木叢呢？

正如上述的瓢蟲例子一樣，答案由邊際價值定理得出。通過做類似於瓢蟲實驗的實驗，科學家Richard Cowie在1977年發現邊際價值理論可以正確預測大山雀放棄灌木叢的時間。

放棄交配

對一隻雄性糞蠅來説，知道自己和一個雌性糞蠅交配多久代表一種典型的權衡，即當前有保障的回報，和一個不確定、但可能會獲得更大的收益。（譯者注：糞蠅生殖過程存在精子競爭（Sperm competition），雌性會與多個雄性交配，每隻雄性要儘可能地置換其他雄性的精子。）雄性糞蠅與雌性糞蠅交配的時間越長，那麼之前與這隻雌蠅交配的其它雄蠅的精子會被替換的越多，並且這隻雌蠅與其它雄蠅交配的機會會越少。換句話説，這隻雄性交配的每一分鐘，都本可以用來和其他雌蠅交配的。

我們可以發現，尋找新的雌蠅所花費的時間，和前面例子中尋找新的食物來源（新蚜蟲和新灌木叢）是類似的，和一隻雌蠅交配的時間對應一個增加但是增量減少的收益。因此，邊際價值定理能夠預測一個雄性的糞蠅應當和每個雌性交配多久以保證儘可能多的後代，對此結果我們不應感到驚訝。1976年，科學家G. A. Parker 和 R. A. Stuart 觀察到雄性糞蠅和每隻雌性糞蠅的交配時間為36分鐘，和邊際價值定理預測的41分鐘相當。

蜜蜂會因太忙而效率低下嗎？

隨着蜜蜂收集越來越多的花粉，將花粉帶回蜂巢所消耗的能量也會增加。每隻蜜蜂都會面臨的困境是：蜜蜂什麼時候應該停止採集花粉返回蜂巢呢？

在一個極端的情況下，如果蜜蜂僅僅採集了一粒花粉後就返回，那麼幾乎肯定的往返蜂巢所消耗的能量會超過從花粉粒中獲得的能量；另一個極端情況是，如果蜜蜂收集了大量的花粉，那麼花粉會收集得很快，但是在飛回蜂巢的路上所消耗的能量將會佔據從花粉中獲得能量的很大一部分比例。兩個極端情況之間有一個恰到好處的承載量——它為飛行中消耗的每一卡路里提供了（因採集花粉而獲取的）最大能量。值得注意的是，蜜蜂連續採集花朵導致負載變多，收益是遞減的。