數學家買彩票中獎的幾率會比普通人更高嗎?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-06-27 10:18
 撰文 | 張天蓉
撰文 | 張天蓉
如今,“概率”一詞在我們的生活中隨處可見,被人們使用得越來越廣泛和頻繁。因為這是一個越來越多變的世界: 一切都在變化,一切都難以確定。我們的世界可以説是由變量構成的,其中包括很多決定性變量。比如新聞説: “北京時間2016年11月3日20時43分,長征五號在海南文昌成功發射”,這裏的時間、地點都是確定的決定性變量。
然而,我們的生活中也有許多難以確定的隨機變量,比如明天霧霾的程度,或某公司的股票值,等等,都是不確定的隨機變量。
隨機變量不是用固定的數值表達,而是用某個數值出現的概率來描述。正因為處處都有隨機變量,所以處處都聽見“概率”一詞。你打開電視聽天氣預報,看看今天會不會下雨,氣象預報員告訴你説: 今天早上8點鐘的“降水概率”是90%;你到手機上查詢股市中的某種股票,你得到的信息可能是這種股票3個月之後翻倍的概率是67%;你滿懷期望地買了50張彩票,朋友卻告訴你,傻瓜才去白花這50塊錢,因為你中獎的概率只有一億分之一……
 圖源:pexls
圖源:pexls
生活中“概率”這個詞太常見了,以至於人們不細想也大概知道是個什麼意思,比如説,最後一個例子中,0.03%的惡性概率的意思不就是説,“10000個這樣的肉瘤中,只有3個才會是惡性的”嗎?因此,在經典意義上,概率就可以被粗糙地定義為事件發生的頻率,即發生次數與總次數的比值。更準確地説,是總次數趨於無限時,這個比值趨近的極限。
 圖源:pexls
圖源:pexls
雖然“概率”的定義不難懂,好像人人都會用,但你可能不知道,概率計算的結果經常違揹我們的直覺,概率論中有許多難以解釋、似是而非的悖論。不能完全相信直覺!我們的大腦會產生誤區和盲點,就像開汽車的駕駛員視覺中有“盲點”,需要幾面鏡子來克服一樣,我們的思維過程中也有盲點,需要通過計算和思考來澄清。概率論是一個經常出現與直覺相悖的奇怪結論的領域,連數學家也是稍有不慎便會錯得一塌糊塗。現在,我們就首先舉例説明經典概率中的一個悖論,叫作“基本比率謬誤(base rate fallacy)”。
我們從一個生活中的例子開始。
王宏去醫院做化驗,檢查他患上某種疾病的可能性。其結果居然為陽性,把他嚇了一大跳,趕忙在網上查詢。網上的資料説,檢查總是有誤差的,這種檢查有“1%的假陽性率和1%的假陰性率”。
這句話的意思是説,在得病的人中做檢查,有1%的人是假陰性,99%的人是真陽性。而在未得病的人中做檢查,有1%的人是假陽性,99%的人是真陰性。於是,王宏根據這種解釋,估計他自己得了這種疾病的可能性(即概率)為99%。王宏想,既然只有1%的假陽性率,99%都是真陽性,那我在人羣中已被感染這種病的概率便應該是99%。
可是,醫生卻告訴他,他在普通人羣中被感染的概率只有0.09(9%)左右。這是怎麼回事呢?王宏的思路誤區在哪裏?
 圖源:pexls
圖源:pexls
醫生説: “99%?哪有那麼大的感染概率啊。99%是測試的準確性,不是你得病的概率。你忘了一件事: 被感染這種疾病的正常比例是不大的,1000個人中只有一個人患病。”
原來這位醫生在行醫之餘,也喜愛研究數學,經常將概率方法用於醫學上。
他的計算方法基本上是這樣的:因為測試的誤報率是1%,1000個人將有10個被報為“假陽性”,而根據這種病在人口中的比例 (1/1000=0.1%),真陽性只有1個,所以,大約11個測試為陽性的人中只有一個是真陽性(有病)的,因此,王宏被感染的概率大約是1/11,即0.09(9%)。
王宏思來想去仍感到糊塗,但這件事激發了王宏去重温他之前學過的概率論。經過反覆閲讀,再思考琢磨醫生的算法之後,他明白了自己犯了那種叫作“基本比率謬誤”的錯誤,即忘記使用“這種病在人口中的基本比例(1/1000)”這個事實。
談到基本比率謬誤,我們最好是先從概率論中著名的貝葉斯定理説起。
托馬斯·貝葉斯(Thomas Bayes ,1701-1761)是英國統計學家,曾經是個牧師。貝葉斯定理是他對概率論和統計學做出的最大貢獻,是當今人工智能中常用的機器學習的基礎框架,它的思想之深刻遠超一般人所能認知,也許貝葉斯自己生前對此也認識不足。因為如此重要的成果,他生前卻並未發表,是在他死後的1763年才由朋友發表的。
粗略地説,貝葉斯定理涉及兩個隨機變量A和B的相互影響,如果用一句話來概括,這個定理説的是: 利用B帶來的新信息,應如何修改B不存在時A的“先驗概率”P(A),從而得到B存在時的“條件概率”P(A|B),或稱後驗概率,如果寫成公式::
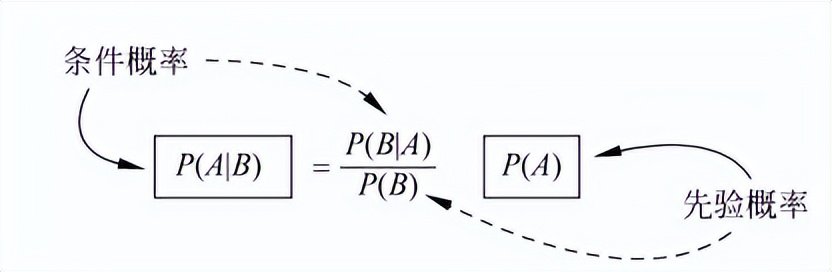 這裏先驗、後驗的定義是一種約定俗成,是相對的。比如説也可以將A、B反過來敍述,即如何從B的先驗概率P(B),得到B的“條件概率”P(B|A),見圖中虛線所指。
這裏先驗、後驗的定義是一種約定俗成,是相對的。比如説也可以將A、B反過來敍述,即如何從B的先驗概率P(B),得到B的“條件概率”P(B|A),見圖中虛線所指。
不要害怕公式,通過例子,我們就能慢慢理解它。
例如,對前面王宏看病的例子,隨機變量A表示“王宏得某種病”;隨機變量B表示“王宏的檢查結果”。先驗概率P(A)指的是王宏在沒有檢查結果時得這種病的概率(即這種病在公眾中的基本概率0.1%);而條件概率(或後驗概率)P(A|B)指的是王宏“檢查結果為陽性”的條件下得這種病的概率(9%)。如何從基本概率修正到後驗概率的?我們待會兒再解釋。
貝葉斯定理是18世紀的產物,200來年用得好好的,卻不想在20世紀70年代遇到了挑戰,該挑戰來自於丹尼爾·卡尼曼(Daniel Kahneman)和特維爾斯基(Tversky)提出的“基本比率謬誤”。前者是以色列裔美國心理學家,2002年諾貝爾經濟學獎得主。基本比率謬誤並不是否定貝葉斯定理,而是探討一個使人困惑的問題: 為什麼人的直覺經常與貝葉斯公式的計算結果相違背?如同剛才的例子所示,人們在使用直覺的時候經常會忽略基礎概率。
卡尼曼等人在他們的文章《思考,快與慢》中舉了一個出租車的例子,來啓發人們思考這個影響人們“決策”的原因。我們不想在這裏深談基本比率謬誤對“決策理論”的意義,只是借用此例來加深對貝葉斯公式的理解。
假如某城市有兩種顏色的出租車: 藍色和綠色(市場佔有比例為15:85)。一輛出租車夜間肇事後逃逸,但還好當時有一位目擊證人,這位目擊者認定肇事的出租車是藍色的。但是,他“目擊的可信度”如何呢?公安人員在相同環境下對該目擊者進行“藍綠”測試得到: 80%的情況下識別正確,20%的情況不正確。也許有讀者立刻就得出了結論: 肇事車是藍色的概率應該是80%吧。如果你做此回答,便是犯了與上面例子中王宏同樣的錯誤,忽略了先驗概率,沒有考慮在這個城市中“藍綠”車的基本比例。
 圖源:pexls
圖源:pexls
那麼,肇事車是藍色的(條件)概率到底應該是多少呢?
貝葉斯公式能給出正確的答案。首先我們必須考慮藍綠出租車的基本比例(15∶85)。也就是説,在沒有目擊證人的情況下,肇事車是藍色的概率只有15%,這是“A=藍車肇事”的先驗概率P(A)= 15%。現在,有了一位目擊者,便改變了事件A出現的概率。目擊者看到車是“藍”色的。不過,他的目擊能力也要打折扣,只有80%的準確率,即也是一個隨機事件(記為B)。我們的問題是求出在有該目擊證人“看到藍車”的條件下肇事車“真正是藍色”的概率,即條件概率P(A|B)。後者應該大於先驗概率15%,因為目擊者看到“藍車”。如何修正先驗概率?需要計算P(B|A)和P(B)。
因為A=藍車肇事、B=目擊藍色,所以P(B|A)是在“藍車肇事”的條件下“目擊藍色”的概率,即P(B|A) =80%。最後還要算先驗概率P(B),它的計算麻煩一點。P(B)指的是目擊證人看到一輛車為藍色的概率,等於兩種情況的概率相加: 一種是車為藍,辨認也正確;另一種是車為綠,錯看成藍。所以:
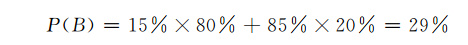 從貝葉斯公式:
從貝葉斯公式:
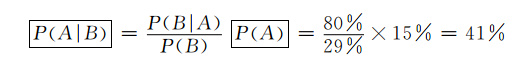 可以算出在有目擊證人情況下肇事車輛是藍色的概率為41%,同時也可求得肇事車輛是綠車的概率為59%。被修正後的“肇事車輛為藍色”的條件概率41%大於先驗概率15%很多,但是仍然小於肇事車為綠色的概率0.59。
可以算出在有目擊證人情況下肇事車輛是藍色的概率為41%,同時也可求得肇事車輛是綠車的概率為59%。被修正後的“肇事車輛為藍色”的條件概率41%大於先驗概率15%很多,但是仍然小於肇事車為綠色的概率0.59。
回到對王宏測試某種病的例子,我們也不難得出正確的答案:
A: 普通人羣中的王宏感染某種病
B: 陽性結果
P(A):普通人羣中感染某種病的概率
P(B|A):陽性結果的正確率
P(A|B):有了陽性結果的條件下,王宏感染某種病的概率
P(B):結果為陽性的總可能性=檢查陽性中的真陽性+檢查陰性中的真陽性
 本文經授權轉載自微信公眾號“原點閲讀”,編輯:張潤昕。本文節選自 張天蓉著《從擲骰子到阿爾法狗:趣談概率》(清華大學出版社,2018年5月)
本文經授權轉載自微信公眾號“原點閲讀”,編輯:張潤昕。本文節選自 張天蓉著《從擲骰子到阿爾法狗:趣談概率》(清華大學出版社,2018年5月)
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。