對數:所有天文學家都應該感謝的數學發現_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-06-28 10:10
數世紀以來,不管對科學家還是對工程師,對數表都是非常實用的工具。現在,因與指數函數的密切聯繫,對數仍充滿了極強的數學吸引力。
撰文 | 理查德·埃爾威斯(Richard Elwes)
翻譯 | 齊瑞紅、房超、於幻
在過去的很多年中,很多人習慣地把對數表放在手邊用來幫助自己進行乘法和除法運算。在20世紀後半葉,便攜計算器最終將對數表推入歷史。但是,在級數和微積分的深層數學領域中,那引人入勝的發現確保了對數本身永不過時。
在16世紀後期,約翰·納皮爾(John Napier)開始研究他最初稱為“人造數”的數。他發現了一種方法,可以將複雜的乘法運算轉化為相當簡單的加法運算。為了求兩個數的乘積,如4587和1962,他首先計算這兩個數的人造數並求它們的和。然後將這兩個人造數的和進行反人造數運算,即計算原數使得它的人造數就是這個和。雖然這個過程沒有涉及乘法運算,但所得的結果確實是原來那兩個數的乘積——8 999 694。
 地震儀用來測量地震的強度。衡量地震強度的、國際上通用的里氏震級表正是對數運算:測定為3 級的地震強度是測定為2級的地震強度的10倍。
地震儀用來測量地震的強度。衡量地震強度的、國際上通用的里氏震級表正是對數運算:測定為3 級的地震強度是測定為2級的地震強度的10倍。
納皮爾的對數
不久後,納皮爾給他的人造數起了一個新的、更好的名字——對數。今天,我們明白對數只是冪運算的逆運算。冪運算指某數與它本身重複相乘,所以,“2的3次方”指3個2相乘,
 布里格斯的對數表
布里格斯的對數表
在約翰·納皮爾發明對數後不久,亨利·布里格斯(Henry Briggs)開始把它轉變成一個有用的工具。因為我們應用十進制數制來表示數,布里格斯選擇以10為底計算對數是比較方便的,並開始着手製作一個“對數表” ——從1到1000 的所有整數的對數。在幾年時間裏,布里格斯和其他數學家將這個表推廣到一個更大的數集上。
當然,對於大部分整數來説,它們的對數都不是整數,所以研究者不得不給出他們求得的對數的精確程度。在18世紀後期,加斯帕德·德普羅尼(Gaspard de Prony)監督製作了一個特殊的數學用表,這個數學用表多達17大本雙開卷,包括最大到200 000的正整數的對數,精確到小數點後第19位(對於較大的數,精確到第24位)。
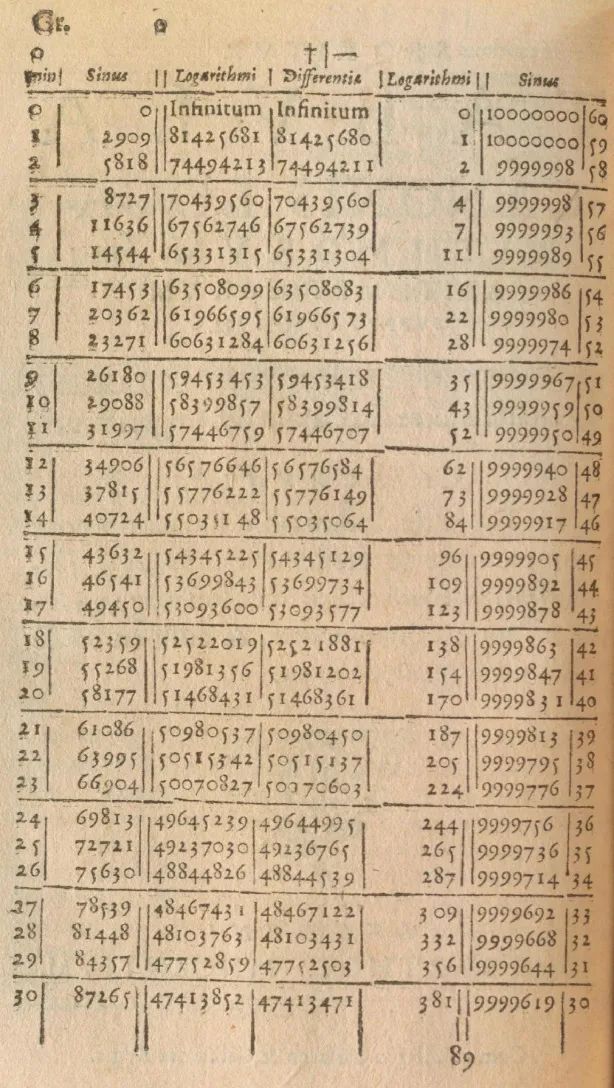 取自約翰·納皮爾 1614 年的專著《奇妙的對數表的描述》裏用的一張最早的對數表。約翰·納皮爾研究的是後來被稱為“自然對數”的對數,而亨利·布里格斯研究的是以10為底的對數——後來被稱為“常用對數” 。
取自約翰·納皮爾 1614 年的專著《奇妙的對數表的描述》裏用的一張最早的對數表。約翰·納皮爾研究的是後來被稱為“自然對數”的對數,而亨利·布里格斯研究的是以10為底的對數——後來被稱為“常用對數” 。
自然對數
自從納皮爾發現對數以來,對數學家來説對數非常有用。就像傑出的科學家皮埃爾-西蒙·拉普拉斯(Pierre-Simon Laplace)所説的:“對數的發現通過節省勞動使天文學家的壽命翻倍。”但是,對數的數學意義比它作為計算工具的意義更為重要和深遠。在1650年,皮耶特羅·曼戈裏(Pietro Mengoli)首次意識到這一點。他的有關級數的研究與他在對數方面的興趣出乎意料地結合在一起。
 這個交錯級數有一個確定的極限,約等於0.693147。曼戈裏證明了這個極限數就是 2 的自然對數(通常記作In2,雖然讀成log2)。自然對數像其他的任何對數一樣,只是對底數有一個特殊選擇,以e為底數,e約等於 2.71828。確實,正是通過自然對數和曼戈裏的結論,數學中最重要的函數之一——指數函數,開始嶄露頭角。
這個交錯級數有一個確定的極限,約等於0.693147。曼戈裏證明了這個極限數就是 2 的自然對數(通常記作In2,雖然讀成log2)。自然對數像其他的任何對數一樣,只是對底數有一個特殊選擇,以e為底數,e約等於 2.71828。確實,正是通過自然對數和曼戈裏的結論,數學中最重要的函數之一——指數函數,開始嶄露頭角。
的確,對更準確的對數表的尋找有力地推動了抽象級數理論的發展。在1668年,尼古拉斯·墨卡託(Nikolaus Mercator)出版了名為《對數技術》的著作, 在此著作中,他發現了自然對數的級數公式:
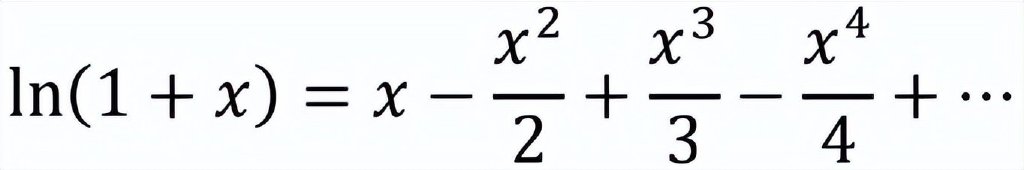 這個美麗的定理正是曼戈裏結果的推廣,曼戈裏的結果對應於x=1的特殊情形。
這個美麗的定理正是曼戈裏結果的推廣,曼戈裏的結果對應於x=1的特殊情形。
微積分和對數
墨卡託的定理暗示了自然對數的“自然”,但是一個更完整的故事需要用牛頓和萊布尼茨的微積分理論來訴説。
 本文經授權摘自《圖解數學簡史:數學世界中不可不知的100個重大突破》第26篇《對數》。
本文經授權摘自《圖解數學簡史:數學世界中不可不知的100個重大突破》第26篇《對數》。
↓↓前往“返樸”公眾號,點擊文末左下角“閲讀原文“購買↓↓
 特 別 提 示
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權説明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。