三次方程的不堪過往_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-07-14 11:06
撰文 | Hemanth
翻譯 | C&C
審校 | zhenni
 左邊這位尼科洛·豐坦納(Niccolò Fontana),也被稱為塔爾塔利亞(Tartaglia)。他與吉羅拉莫·卡爾達諾(Gerolamo Cardano)在解決立方方程問題上做出了貢獻,但也在這條道路上成為了敵人。
左邊這位尼科洛·豐坦納(Niccolò Fontana),也被稱為塔爾塔利亞(Tartaglia)。他與吉羅拉莫·卡爾達諾(Gerolamo Cardano)在解決立方方程問題上做出了貢獻,但也在這條道路上成為了敵人。
歷史上充滿了反目成仇的競爭:愛迪生和特斯拉,哈丁(Harding)和凱麗甘(Kerrigan,皆為滑冰運動員)等等。16世紀意大利數學家卡爾達諾和尼科洛·豐坦納 (後者更廣為人知的名字是塔爾塔利亞,意為“口吃者”,因少年時面部被法國士兵的劍得傷後説話困難而名)之間的衝突同樣具有戲劇性。起因就是:三次方程。
大多數高中生都知道如何用求解二次方程,如x2-x-3=0。ax2+bx+c=0這樣方程的解、或者説根是:
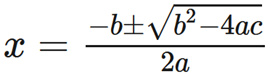 對於更高次(x的冪次更大)的方程是否有類似的公式呢?從本質上講,在卡爾達諾、塔爾塔利亞和他們同時代的人之前,就已經有了解決這個問題的任務。
對於更高次(x的冪次更大)的方程是否有類似的公式呢?從本質上講,在卡爾達諾、塔爾塔利亞和他們同時代的人之前,就已經有了解決這個問題的任務。
像上面這些抽象的符號表達式和熟悉的操作方法的現代代數可以追溯到17世紀,比這些學者的時代晚了很久。但是代數思想,以及解決我們所認為的線性和二次方程的能力,在之前的幾千年裏一直髮展緩慢。
在16世紀,代數方程仍然是用文字而不是符號來表達的,所有的係數都必須是非負的,因為數

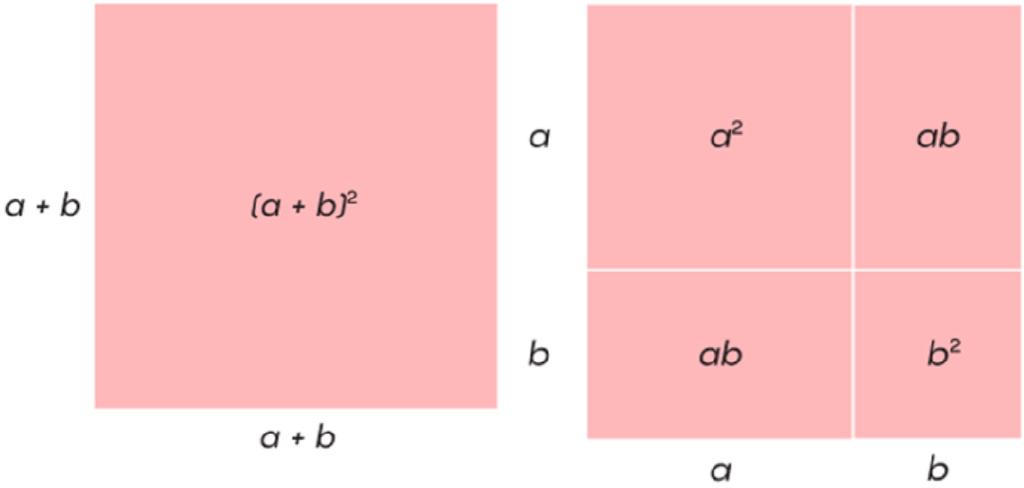 同樣地,將邊長為t的立方體分解為6個方塊可以有下面的表達:
同樣地,將邊長為t的立方體分解為6個方塊可以有下面的表達:
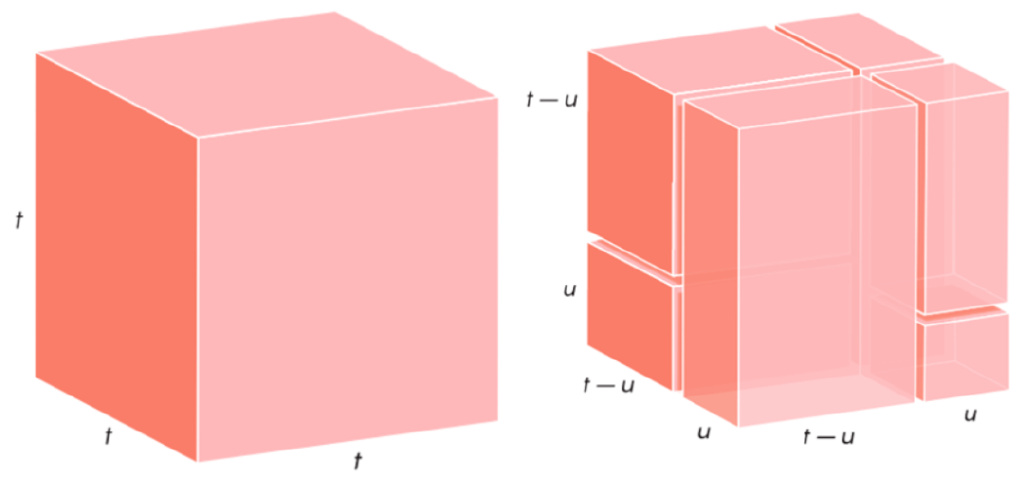
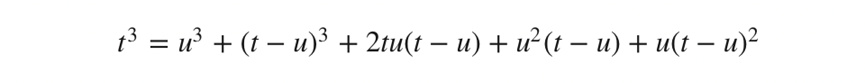 (t>u)。
(t>u)。
希皮奧內·德爾·費羅(Scipione del Ferro)是16世紀早期博洛尼亞大學的一位教授,他是第一個在求解三次方程方面取得重大進展的人。不幸的是,由於當時奇怪的學術保密文化,我們並不知道他的所有成就。學者們不會急於發表自己的研究成果,也不會陶醉於證明一個定理或解決一個問題獲得的認可,他們會互相挑戰,進行“數學決鬥”:互相發送具有挑戰性的問題,誰解決得最多,誰就獲勝。勝利者往往會獲得職業發展和更多的學生。因此,這些發現有時會被儲存起來,成為將來在競賽中使用的秘密武器。
當c和d為正時,費羅可以解出x3+cx=d的方程。像這樣沒有平方項的三次方程被稱為“虧損立方(depressed cubic)方程”。儘管16世紀的數學家不會用這種表達式,但費羅證明了其中一個根是:
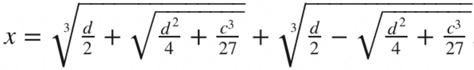 這個現代公式適用於任何虧損立方方程,但由於不同係數符號的三次方程被認為是不同問題,因此費羅的解不能直接應用到其他虧損立方方程。我們只知道費羅解出這些三次方根是因為他把這個技術教給了他的學生菲奧爾(Antonio Fior),後者在費羅死後吹噓他能解出這樣的方程。
這個現代公式適用於任何虧損立方方程,但由於不同係數符號的三次方程被認為是不同問題,因此費羅的解不能直接應用到其他虧損立方方程。我們只知道費羅解出這些三次方根是因為他把這個技術教給了他的學生菲奧爾(Antonio Fior),後者在費羅死後吹噓他能解出這樣的方程。
與此同時,自學成才的塔爾塔利亞發現了另一種形式的三次方程的解法——通過減去線性項cx。這為菲奧爾和塔爾塔利亞之間的數學對決奠定了基礎。1535年,他們交換了30個問題,期限是一個半月。塔爾塔利亞給菲奧爾提供了各種各樣的問題,而數學上較弱的菲奧爾採用了“所有雞蛋都放在一個籃子裏”的策略,給塔爾塔利亞提出了30個虧損三次方程。就在截止日期的前幾天,塔爾塔利亞想出瞭解決這些問題的方法,並在兩個小時內完成了所有問題;與此同時,菲奧爾沒有解決任何問題。塔爾塔利亞成功的消息傳遍了整個意大利,而被羞辱的菲奧爾也從人們的視野中消失了。
當時的普遍看法是,解出立方方程是不可能的,所以塔爾塔利亞的成就震驚了卡爾達諾。
卡爾達諾是當時的一位備受追捧的醫生,但他脾氣暴躁、賭博、與行為不端的兒子鬥爭、在宗教裁判所入獄等等,被一個又一個麻煩所困擾。然而他仍然在數學、醫學、哲學、宗教、音樂和物理方面做出了貢獻。幾十年後,戈特弗裏德·萊布尼茨(Gottfried Leibniz)寫道,“卡爾達諾是一個偉大的人,因為他具有的缺點;如果沒有這些缺點,他將是無與倫比的。”他的作品集長達7000頁,其中包括對概率論的首次嚴肅研究。
卡爾達諾試圖複製塔爾塔利亞在立方上的成功,但失敗了,所以他開始施壓説服塔爾塔利亞分享他的方法,甚至發誓承諾保密:
我以《神聖的福音》和我作為紳士的信仰向你發誓,如果你把你的發現告訴我,我不僅永遠不會公佈,而且作為一個真正的基督徒,我保證把它們用密碼記錄下來,這樣在我死後就沒有人能理解了。
最終,在1539年,塔爾塔利亞妥協了,與卡爾達諾分享了他求解虧損三次方程的技巧。雖然沒有分享完整的證明,但對於聰明的卡爾達諾來説,僅僅知道這個方法就足以發現潛在的數學原理。不久之後,卡爾達諾就能解出任何一個虧損三次方程。他觀察到了這種替換:
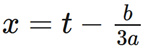
 儘管他對塔爾塔利亞發了誓,但卡爾達諾還是把這些結果告訴了他才華橫溢的助手盧多維科·費拉里(Ludovico Ferrari)。他一開始只是卡爾達諾的僕人,但最終在數學上可以與卡爾達諾平起平坐。通過幫助卡爾達諾研究三次方程,他在代數上非常熟練,發現瞭如何將四次方程(一元四次)簡化為三次方程。因此,卡爾達諾和費拉里得以求解任何四次或四次以下的方程。
儘管他對塔爾塔利亞發了誓,但卡爾達諾還是把這些結果告訴了他才華橫溢的助手盧多維科·費拉里(Ludovico Ferrari)。他一開始只是卡爾達諾的僕人,但最終在數學上可以與卡爾達諾平起平坐。通過幫助卡爾達諾研究三次方程,他在代數上非常熟練,發現瞭如何將四次方程(一元四次)簡化為三次方程。因此,卡爾達諾和費拉里得以求解任何四次或四次以下的方程。
卡爾達諾認識到這些成就的重要性,並迫切希望公佈這些結果。但它們都是由塔爾塔利亞種下的種子長出來的,這樣做會違揹他的誓言。
1543年,在一次博洛尼亞之旅中,卡爾達諾在費羅的手稿中看到,他比塔爾塔利亞更早地解決了虧損三次方程問題。在卡爾達諾看來,這個發現解除了他對塔爾塔利亞的義務。兩年後,卡爾達諾出版了《大術》(Ars Magna),其中包括他和費拉里關於三次和四次方程的研究。
儘管卡爾達諾在書中承認了塔爾塔利亞的工作,但他勃然大怒,指控卡爾達諾盜竊並違背了神聖的誓言。卡爾達諾則把這些指責留給了他忠誠的攻擊犬費拉里。激烈的論戰以公開小冊子的形式持續了好幾個月,導致了塔爾塔利亞和費拉里之間的數學對決,並最終在費拉里的家鄉米蘭進行了公開辯論。塔爾塔利亞更願意與受人尊敬的卡爾達諾作戰,但被拒絕了。儘管留存的細節很少,但針對塔爾塔利亞的攻擊非常激烈,尤其是在對手家鄉喧鬧的人羣中。到第二天繼續辯論的時候,塔爾塔利亞卻不見了,因為他已經離開了米蘭。
費拉里收到了大量的工作邀請,而塔爾塔利亞的名聲毀了。儘管除了那些與三次冪有關的成就之外,塔爾塔利亞還有許多顯著的成就,但他死時身無分文,無人問津;而卡爾達諾卻獲得了永恆的名譽,許多人認為《大術》的出版標誌着現代數學的開始。
 1824年,尼爾斯·阿貝爾(Niels Abel)首次完整地證明了這一事實,比《大術》晚了近三個世紀。在1830年,18歲的政治煽動者埃瓦里斯·迦羅瓦(Évariste Galois)通過給出任意階多項式何時可解的確切標準,擴展了這項工作。雖然伽羅瓦在兩年後死於一場決鬥(用槍而不是數學的決鬥),但他對數學的貢獻是巨大的。
1824年,尼爾斯·阿貝爾(Niels Abel)首次完整地證明了這一事實,比《大術》晚了近三個世紀。在1830年,18歲的政治煽動者埃瓦里斯·迦羅瓦(Évariste Galois)通過給出任意階多項式何時可解的確切標準,擴展了這項工作。雖然伽羅瓦在兩年後死於一場決鬥(用槍而不是數學的決鬥),但他對數學的貢獻是巨大的。
這些“不可能”的結果並不是故事的結局。數學家仍然在研究多項式、它們的根和性質。大衞·希爾伯特(David Hilbert)在1900年提出了一個關於七次多項式根的著名問題。上世紀50年代就被認為已經解決了的問題,現在又重新引起了人們的興趣。據推測,現代數學家可以在這個問題上取得新的進展,還不必重演圍繞三次冪的競爭。
本文經授權轉載自微信公眾號“中科院物理所”,編輯:zhenni。
原文鏈接:
https://www.quantamagazine.org/the-scandalous-history-of-the-cubic-formula-20220630/
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。