今天的文章只有一點點_風聞

原創：中科院物理所

點

大約是在今年一月中旬, 我抬起頭來, 第一次看見了牆上的那個斑點. 為了要確定是在哪一天, 就得回憶當時我看見了些什麼. 現在我記起了爐子裏的火, 一片黃色的火光一動不動地照射在我的書頁上; 壁爐上圓形玻璃缸裏插着三朵菊花. 對啦, 一定是冬天, 我們剛喝完茶, 因為我記得當時我正在吸煙, 我抬起頭來, 第一次看見了牆上那個斑點…

《牆上的斑點》 弗吉尼亞·伍爾芙

這是一個點:

為了和伍爾芙的那篇名作呼應, 我托起了相機, 拿起了塵封已久的手繪板, 第一次在軟件裏編輯了這張圖片. 為了要確定這張圖片的信息, 我就得打開軟件的文件屬性面板. 現在我記起了sRGB的色彩模式, 以及…

通常在某些學科中(比如數學和物理裏), 點沒有大小. 所以下面的也算是一種點:

右邊的點的畫紋是多麼的漂亮和美觀, 它的形狀和朝向又是這樣的優雅和… (咳, 吹不下去了. )

但是如果你把鏡頭移開一點點, 讓畫面變得更大一些, 於是之前(右邊)的點也沒有那麼的“龐大”了.

可是, 這般針眼般大小是點, 米粒般大小是點, 拳頭般大小也是點, 那麼到底什麼才算是點? 這個時候不妨我們帶上“戰術目鏡”, 把所見的一切東西的“戰鬥力數值”都顯示在一個表格裏面:

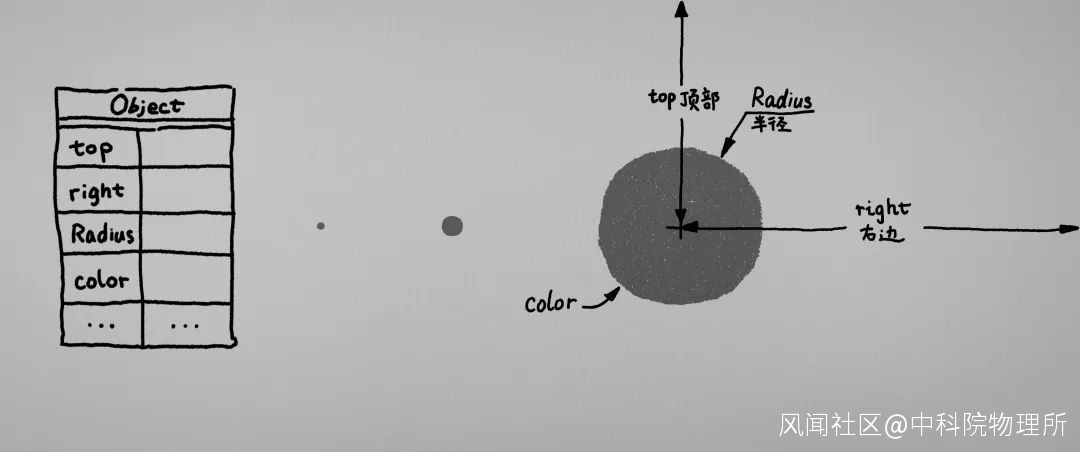
假如對任何一個物體, 我們都能夠想一個方法把它的信息全部寫進一個表格裏面. 那麼在某種程度上來説, 我們便可以將物體用表格來等效地表達和代替.

但是現實世界中, 要描述一個物體可能需要非常多的信息, 即一個物體對應了一個非常多行的表格. 處理眾多的信息是非常麻煩的一件事情, 所以一個簡單的思路就是: 只關注一部分的信息.

假如我們只保留物體的位置(也就是上圖中的top和left的信息, 或者專業一點, 叫做“座標”. )信息, 那麼不論物體的其他特徵再怎麼花裏胡哨, 在我們的眼中, 也不過就是一個簡化的座標 – 或者説, 一個抽象的“點”.

但有時候, 我們也可以不那麼“激進”, 可以多保留一些信息, 比如質量(比如一個5公斤的點), 速度(比如一個5cm/s的豎直下落的點), 角動量(想象一個旋轉的點着實有些困難)等等. 於是我們就得到了“五彩斑斕”的點:

點成精了(bushi

假如你想要一些別的觀點:

我們可以將上面的投影看作是一種將在信息空間中的代表物體的信息的向量投影到位置空間和其他的空間的直和的新的空間的運算——為了簡化計算量; 又或者是處於觀測限制, 只能夠觀測到一部分有限的信息——為了從有限的信息中儘可能地還原出原本的物體的信息.

點, 點

線之界是點 <凡線有界, 兩界必是點. >

《幾何原本》 歐幾里得(著) 瑪利亞 徐光啓(譯)

如果我們目前只考慮物體的位置, 忽略其他的信息, 然後來看下面的圖:

我們會發現, 雖然在上面的那件文物作品上的花紋僅僅只是最樸素的點(戳戳), 但是一個個的點組合在一起, 卻能夠形成有規律的圖案: 三角形, 環帶等等. 在某種程度上來説, **原本我們通過”點”的模型簡化了的信息, 在點與點之間的關係中, 又重新被表現了出來.**那麼我們為什麼不反過來思考: 能否把一些複雜的圖形, 對象, 物體來用一些簡單的基本的”點”(我們前面應該很熟悉這個點的故事了吧. )來表示呢?

眾所周知, 有色差的地方就能夠有Bad Apple…

啊, 不是. 是兩點確定一條直線(大概). 就像是《超能陸戰隊》中的大白的眼睛一樣:

大白: ? (好吧, 我不會畫畫

於是**只要有兩個點, 我們就能夠知道同樣在直線上的其他點的位置信息了.**這樣的方式是多麼的便利啊! 並且既然會畫了直線, 那麼距離畫曲線還會遠麼? (古人云: “三歲小兒皆可握筆塗鴉, 以直代曲, 有大拙之美. ”Bushi)

上圖中沒有一根曲線被使用, 除非我手抖了

於是, 想要用直線來表現曲線(比如上圖中的頭髮”曲線”), 只需要在曲線上選擇合適的特徵點, 然後用直線連接特徵點, 就能夠在一定程度上表現曲線的神韻了. 也就是説, 我們通過用直線上的點來代表曲線上的點的方式來近似地表現曲線. 而倘若我們能夠將特徵點的數量增加到一定的程度, 然後眯上眼睛——看上去這樣的直線就變得像是一條曲線一樣了.

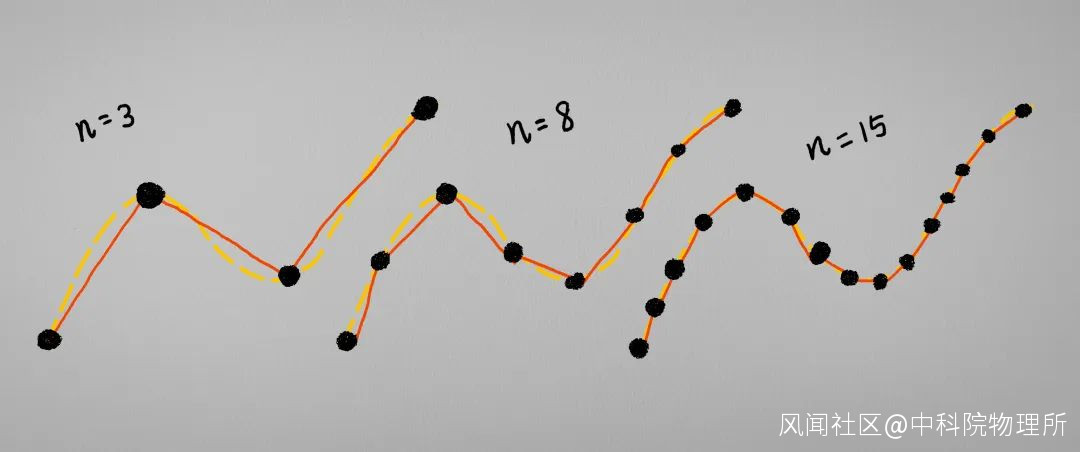
隨着特徵點的數量增加, 直線越來越接近曲線, 於是可以説: 在一定小範圍內, 可以用直線表示曲線

(微積分的思想大概就是這樣的)

也許有槓精會説, 那怎麼可以呢? 我大工匠精神要的就是這手工藝的美妙曲線, 你的直線是工業化的機械的直線, 沒有我工匠精神的靈魂! 我的手捏出來的曲線, 每根線的誤差都不到ε的誤差.

那麼面對這樣的槓精, 我們能做的只有——進一步地增加特徵點的數量, 比如説當特徵點數量n≥N(ε)時, 我們的誤差就會小於ε. 於是我們便可以自豪地邪魅一笑: 直線也能夠逼近曲線. 用數學的語言來説便是:

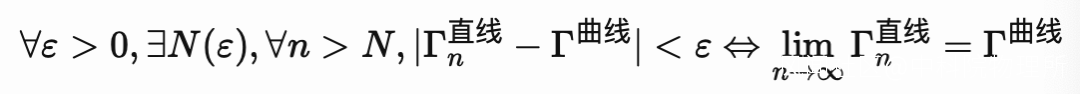
同理, 我們也能夠將這樣的方式應用到曲面, 立體的問題上. (既然你已經學會了一加一了, 那麼請…) 回憶前面”點”的處理方法, 我們會發現, 這樣的選擇特徵點來代表物體的更加複雜的信息和原來的抽象近似是異曲同工的: 都是通過僅保留一部分的信息, 來達到對原始物體的狀態的描述.

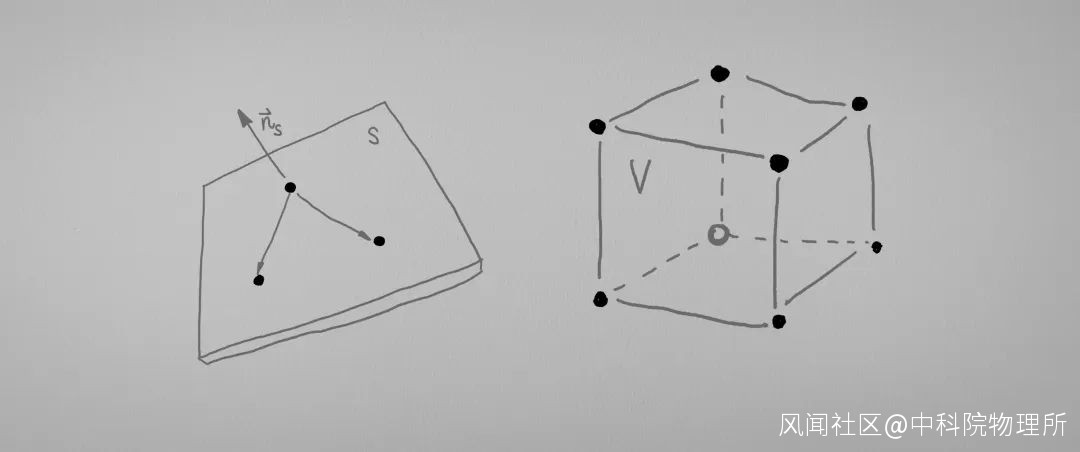
點, 點, 點

If this is to be proved and the type of computer is as I’ve already explained, then it’s going to be necessary that everything that happens in a finite volume of space and time would have to be exactly analyzable with a finite number of logical operations.

Richard P. Feynman, Simulating Physics with Computers,May 7, 1981

(以下是本人渣翻譯, 為了讀者考慮, 上面是原文)

如果存在我(費曼)之前假設的那種通用計算機的話, 那麼(利用計算機來模擬物理)就需要通過在有限的空間和時間中進行有限次的邏輯運算來實現.

理查德 P. 費曼, 用計算機模擬物理, 1981年5月7日

正如我們上面所説的那樣, 為了簡便運算和處理, 我們將物體抽象簡化為點的模型來考慮. 而又為了更好地表現物體的其他信息, 我們可以通過加入更多的點(或者説是引入點與點之間的關係)來承載和表達物體更多的信息.

但是請不要僅僅侷限於如何把數據記錄下來, 格局要打開, 為什麼不問問神奇海螺呢?試試看讓這些數據代替現實中的物體進行一個模擬運動呢? 比如説物理課上的數學公式就是一種用抽象的數據來代替現實中真實物體的方法.

在物理中的數學量(一般)都是一種(隨着時間)連續變化的數學函數. 譬如在佔據物理學大半江山的振子運動方程:

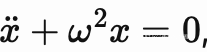
對於一個解

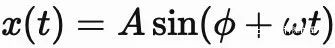
其對應的物理量便是一種隨着時間連續變化的量. 在數學上, 不論多麼精確數值都是可能的 —— 因為sin是一個連續函數. 而在(一般的)物理圖像中, 好像也應該是這麼回事——因為空間是連續的. 如果把這些“連續”的函數畫在圖上的話, 那麼看上去就會像是一條平滑的曲線. (注: 嚴格定義並不是“圖像是平滑曲線的函數是連續函數”. )

但是為什麼我們不借鑑一下前面的”點”的思想, 通過一定的”特徵點”來描述這些物理量的變化關係呢? 於是本來連續的物理量就被分割成了離散的量. 而這樣的東西便可以交給計算機來處理. 於是用計算機來模擬物理世界的問題看起來便十分具有吸引力了.

首先是時間, 假如我們考慮一個簡單的勻速直線運動: x(t) = v t, 那麼在時間軸上選擇一些特徵點進行分割, (就像是用一台相機定格住一瞬的空間), 沿着這些特徵點分割出來的”空間”不妨讓我們看作是一種”狀態”, 根據特定的規則, 從這個時間點跳轉到下一個時間點時, 我們的狀態會發生改變. 用人話來説就是: 從x(t₀)的狀態變化到了x(t₀+Δt)=x(t₀) + v Δt的狀態.

假如你想要一些別的觀點:

不妨將這樣的狀態轉移問題看作是一種拓展版的自動機. 

還記得前面對於精度的那個抬槓問題麼? 同樣的, 我們在模擬的時候也會遇到精度的問題, 如果我們遇到了運動波動非常大的運動, 那麼就需要更多的特徵點. 但是作為摸魚大户, 看到一條几乎平直的線上打滿了點, 而一條蛇形的曲線巧妙地“避開”了點…

點, 點, 點…

那麼最後來一些比較”實在”的例子吧. (參考: Understanding the Finite Element Method (Youtube), 以及《理論力學》梁昆淼)做收尾吧: 如果我們想要了解一個彈性立方體在特定受力下的形狀.

我們將一個立方體看作是具有質量的點的集合. 並且眾所周知, 有彈性(非剛體)的物體在受到外力作用的時候會發生形變. 於是我們不妨在點的基礎上再附加一個信息: 即形變的大小, 假設是一個三維歐幾里得空間(或者三維空間中的直角座標系)中的立方體, 那麼其位移便可以用分量來表示.

眾所周知

有彈性的物體可以被壓縮, 被壓縮的物體會有一種返回原本狀態的”趨勢” —— 即有一個反彈的力(即壓縮後的彈性物體在一定程度上會產生一個近似和壓縮量成正比的回覆力). 用一個叫做”胡克定律”的公式寫出來便是: F = - k δr.

關於胡克定律:

在梁先生的理論力學一書中,這樣定義: “彈性棒伸長或縮短時,任一橫截面兩方的相互作用力F正比於棒的伸長或縮短l.

據維基百科的説法,在最早的發表(來源於對彈簧鐘的製作)中:胡克定律是一串打亂的拉丁字謎: “ceiiinosssttuv” (如果不能確認自己的發現,就在發表時先把自己的發現打亂字母順序後發表,在確認後再公佈結論.嗯,着實是一種方法. ), 真實的順序則為: “ut tensio sic vis”, 即"力如伸長(一般變化)”. (其實這感覺就和我們古代的中國人的文獻一樣了,説得很簡單晦澀,比如"道可道,非常道"之類的,而現代的科學則需要更加嚴格沒有歧義的解釋.這麼説來,我們也算是踩在巨人的肩膀上的發展了. )

不過傳説,牛爵爺的這句"踩在巨人的肩膀上"卻是在對胡克的一種嘲諷——嘲諷胡克的矮小. 但是拋開胡克和牛頓等人的矛盾不談, 胡克卻是是一位非常有光彩的科學家. 在英文的維基百科中是這樣描述胡克的: “polymath”(在中文中則是"博物學家").確實,作為早期的有名的科學家之一,胡克的研究涉獵非常的廣泛,並且對多種科學分支都有基礎性的一些貢獻.

(嘛,某種程度上來説,生得早一些也有一點點的好處. )

而將同一物體的不同部分相互連接在一起, 於是就能夠得到一連串的受力和位移的關係, 將這些關係組合在一起, 那麼我們便能夠知道物體中的力的分佈. 舉個例子(超級簡單的例子):

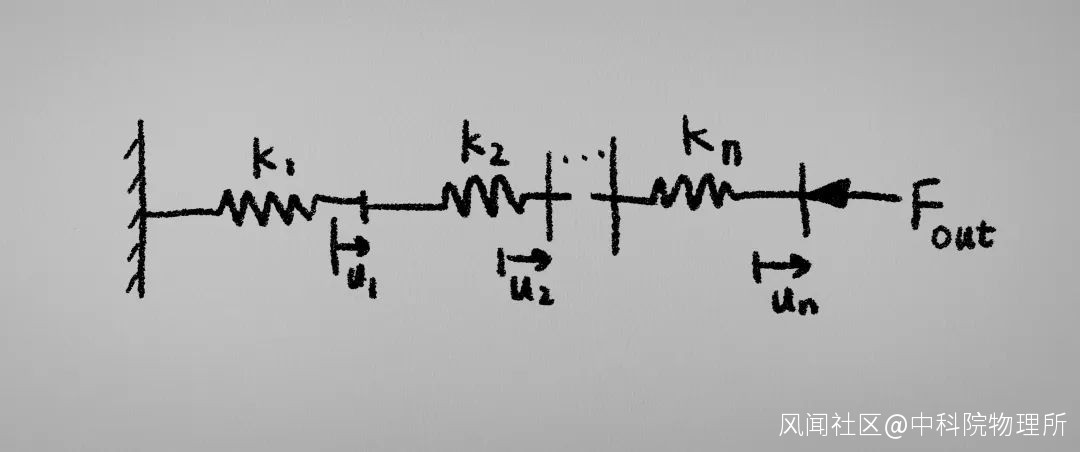
一個簡單的例子, 一堆彈性係數不同的彈簧串聯在一起.

於是我們會説, 這些受力的方程為:

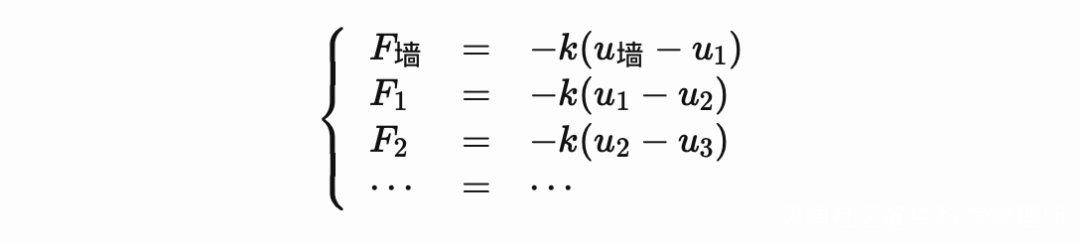
但是對於每一個部分, 都有相互關聯的部分:

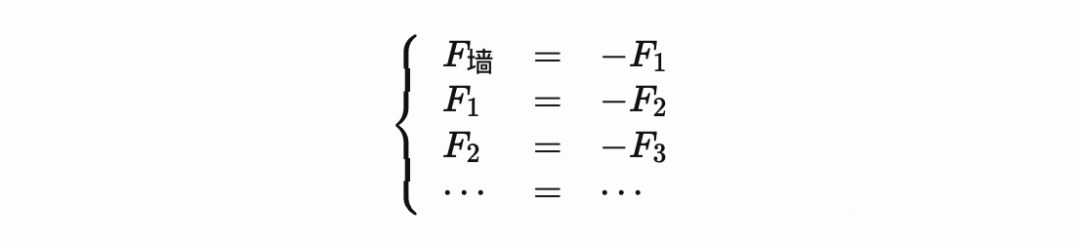
最後, 整體的平衡關係:

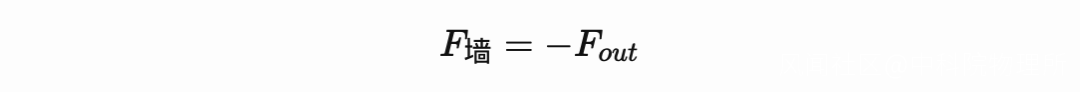
於是我們就能夠計算外力的分佈了.

那麼能不能再複雜一點?

沒問題, 我們只需要將需要考慮的東西擴展一下, 比如説, 這個時候考慮一個在重力場中倒掛的彈簧.

一堆小猴子掛在樹上, 想要撈月亮…

相較於之前的問題, 不難發現變化的只有受力的方程部分:

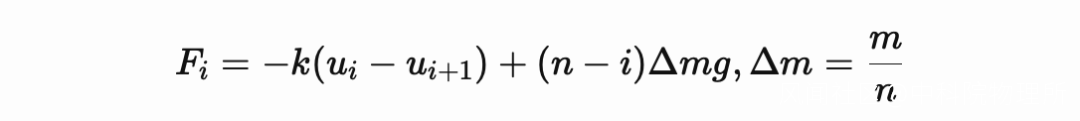
於是就能夠通過這樣的方式來計算最終的結果. (計算過程略? )

關於計算過程以及一些想法:

如果我們把對單個彈簧的受力方程寫成下圖所示的形式:

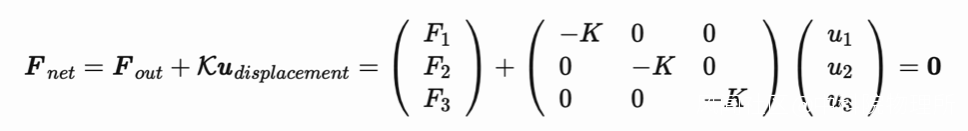
而類似的, 我們可以拓展寫出多個彈簧的受力方程:

於是就能夠計算得到結果. 並且這樣的做法, 還能夠有助於我們考慮更加複雜和一般的問題, 譬如將恢復係數的矩陣寫成一般的形式:

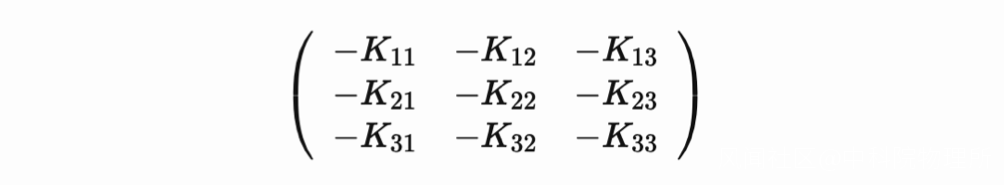
於是就可以表達更加複雜的彈性性質了.

那一個立方體?

在某種程度上來説, 我們可以通過一點點的拓展來將立方體看作是一種對上面的問題的Pro Max版本. 也就是説, 我們可以像這樣將一個立方體進行“離散化”操作:

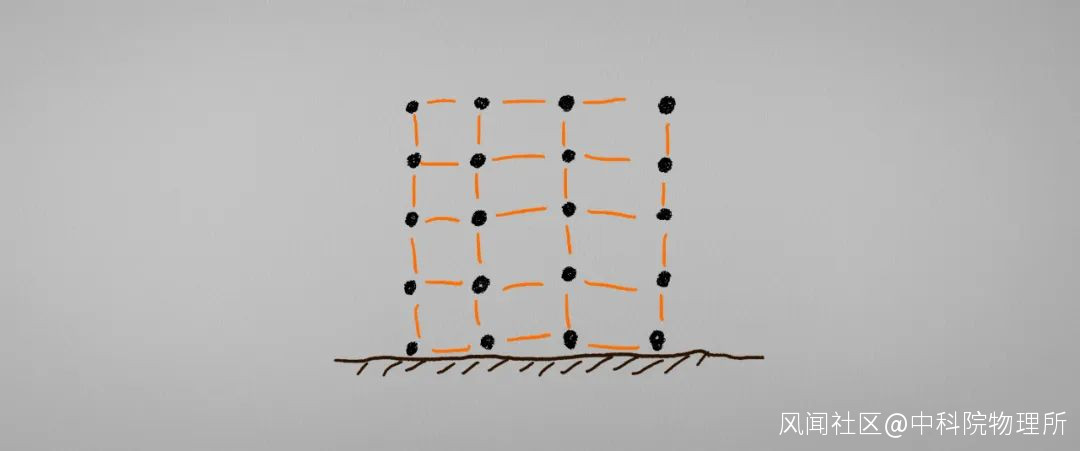
突然想起了MC…

又或者是像下面這樣的圖像:

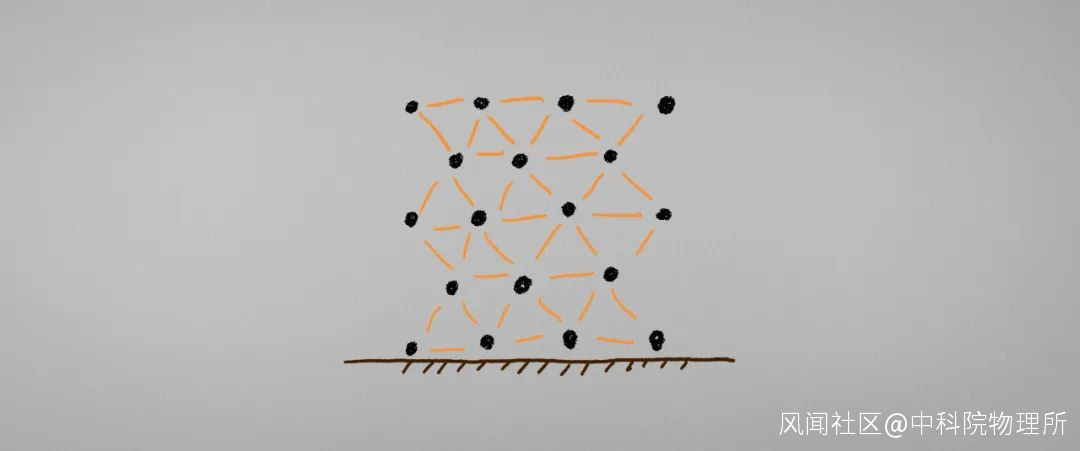
三角形總是讓我想起山上的輸電線的塔…

於是問題就變成了對上面的處理方法的”億點”拓展了. 但是在上面的問題中, 需要計算的東西着實有些多了一些, 所以這個時候我們就可以應用計算機來輔助我們進行模擬計算. 並且我們還能夠發現, 上面的計算過程中, 我們的特徵點並不是像之前分析的那樣: “在變化大的地方密集, 在變化小的地方稀疏”, 而是均勻的分佈的, 這也同樣是一種可以進行優化改進的地方.

這樣的計算方式好像就叫做“有限元分析”. 但是名字不太重要, 我們的想法不過就是將原本複雜的連續的問題通過變成一個個的點(離散化)的方法來減少研究的規模, 來達到簡化計算的目的. 總之你已經學會了1+1了. 那麼不妨試試看… ?