相位，到底是個啥？_風聞

撰文 | 邵曉鵬教授（西安電子科技大學）

在計算光學領域，平生不把“相位”玩，便稱英雄也枉然！相位，是計算光學成像裏繞不開的東西，號稱“凌波微步”的相位大法，是計算光學成像的十八般武藝之一。

今天，我們就來揭開相位的神秘面紗。

平靜的水面扔進一顆石子，會蕩起一圈圈的漣漪；燃燒的火堆後面，能看到影影綽綽變形了的臉；一束激光照射到全息幹板上，能看到栩栩如生的三維立體圖像；滴答走着的鐘表，地上被老大爺抽打着轉了一圈又一圈的陀螺……所有這些，都與 “相位”有關。

可是，説起相位（Phase），大家似乎都感覺到熟悉又陌生。這個詞不僅在計算光學成像中隨處可見，而且在光學、數學和信號處理領域也司空見慣，但好像每次見到都感覺有些不同。我見過很多光學專業的學生會有一個思維定勢，認為相位應該是光波函數的相位，而當他們閲讀一些文獻的時候，見到相位往往就莫衷一是的樣子，手足無措。

那麼計算成像裏的相位都有哪些？相位能帶來什麼？我們還能對相位做點什麼？如何在計算成像中引入相位和解譯相位？

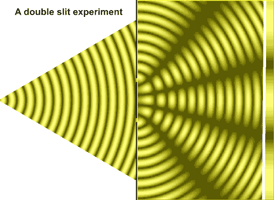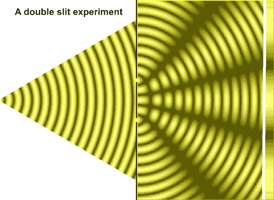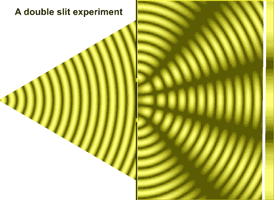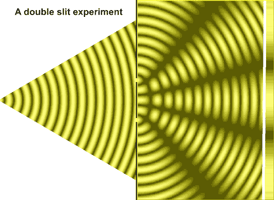相位的多樣性

1 相位到底是什麼？

我們生活在一個充滿各種各樣波的世界裏，要理解相位，首先得了解什麼是波。有些人可能覺得這個問題有些奇怪，這還用問嗎？划船時的水波，廣播裏的聲波，跳繩時的繩波。當然，生活中的還存在着很多波動現象。我們要透過現象看本質，就是我們如何用一套統一的數學語言來描述波。

光是一種電磁波，它滿足波動方程：

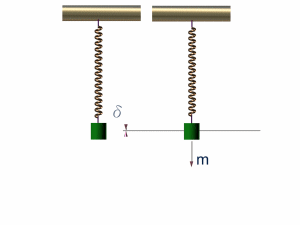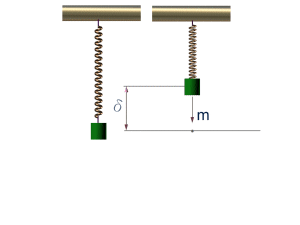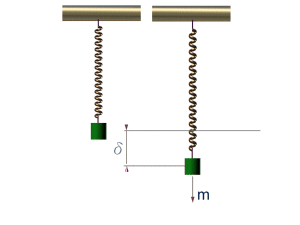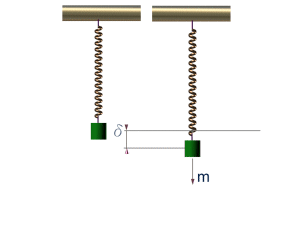
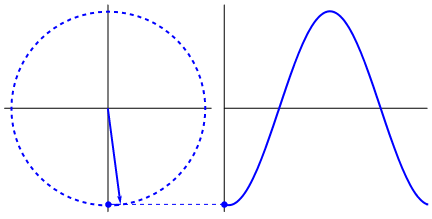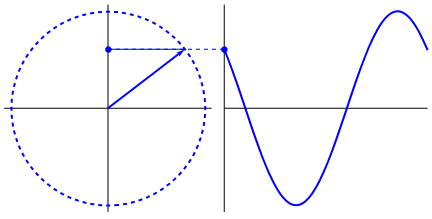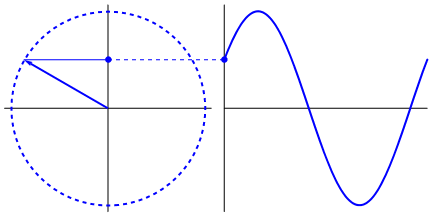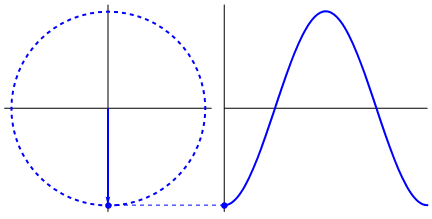簡諧運動的相位與波的相位

之所以講這些枯燥的內容，只是想把來龍去脈搞清楚。

這裏需要總結一下：所有寫成複數形式的式子都有相位，而相位是與幅角相關的一個相對值。你看，這不就簡單了嗎？再強調一下：凡是複數形式的，必有相位；相位是一個相對值，一定要與初始位置一起用。其實，還可以歸納一條：凡是能夠表示成週期性函數的，都有相位。

打個比方，排列整齊的隊伍在一聲“解散”口令後，立馬就成雜亂無序狀；一聲“歸位”令下，很快就又恢復了排列整齊的隊伍。在這裏，每個人都有自己的位置，這個位置就相當於相位。

隊列歸位

因此，你會看到五花八門的各種複數表達式，很顯然，這些複數表達式裏都有相位，只是，你可能不知道這個相位到底表達什麼意思。那我們就來列舉一下計算光學成像中會遇到哪些相位。

第一是大家熟悉的光波函數，有幅值有相位。由於光的探測是強度信息，相位探測都是間接方法測量出來，比如干涉法。自然光的時間相干性和空間相干性都很差，可以認為相位雜亂無章，變化無常，難以記錄。

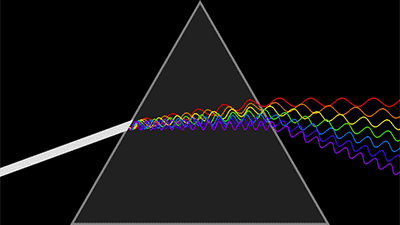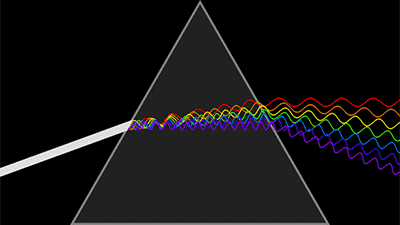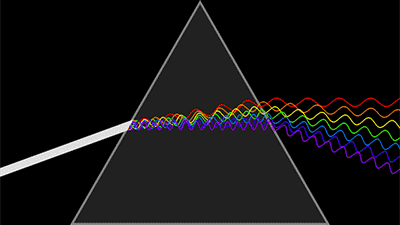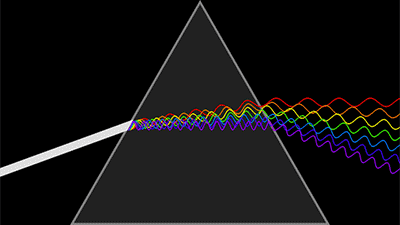
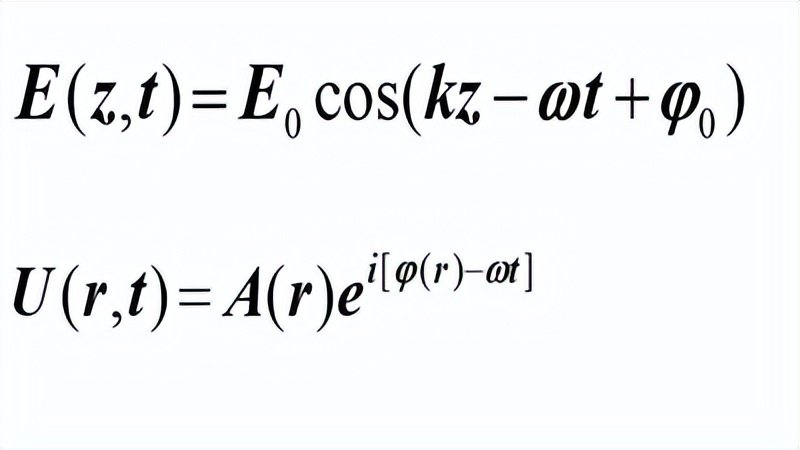光波與波函數

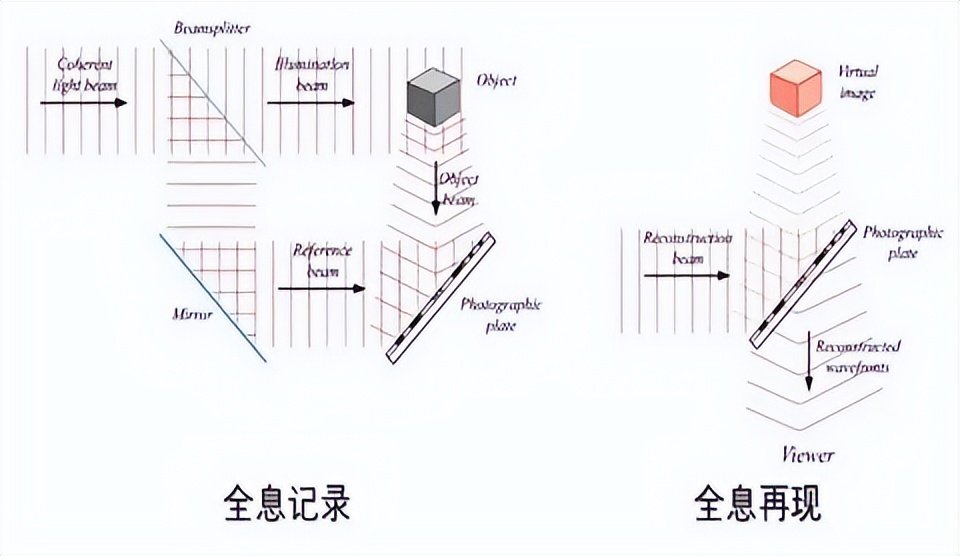
第二是全息，我們知道全息表示形式本身就是複數的，自然有相位；最重要的是，全息記錄的就是相位信息，只需用滿足布拉格條件的再現光照射全息圖就能重建出原始相位。

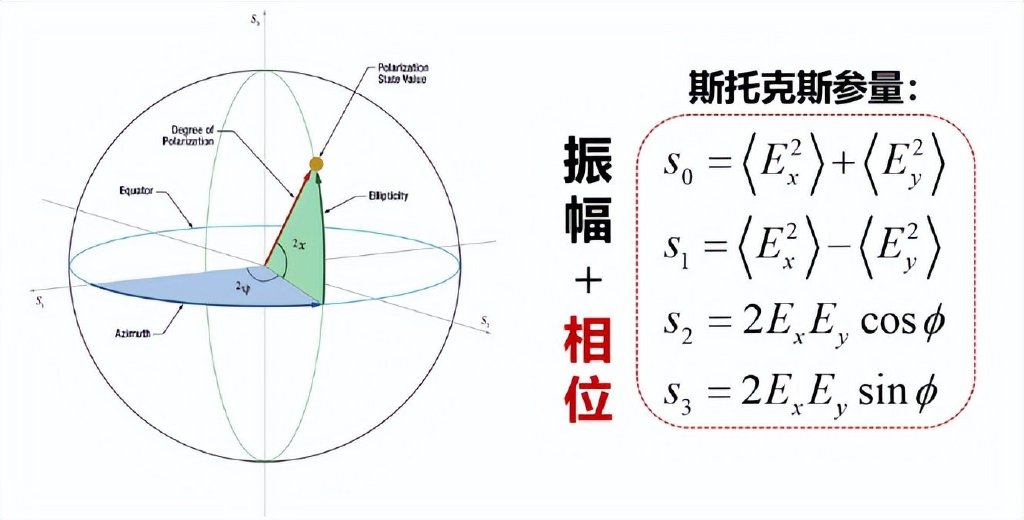
第三是偏振。在第四篇“偏振：古老卻依然很新鮮”一文中我們已經講過，偏振乍一看似乎找不到那個相位，但是深入分析一下就知道，偏振有偏振度和偏振角兩個量，其中偏振角就可以等效看作相位。

第四是結構光成像。我們知道，當平面波投射到物體表面時，遵循菲涅爾定律產生折射和反射，物體表面的起伏會產生相位的變化，將不再是平面波，記錄下此時的波前，便能夠恢復出物體的三維形貌。這是教科書的表述方式，實驗卻沒那麼容易。

我們希望在自然環境中也能夠記錄相位，實現三維成像。其實很簡單，採用結構光照明，典型的就是黑白相間的平行條紋，投射到物體表面，就能看到條紋的形變，這種形變恰恰是我們通過照明的方式引入的相位；記錄下條紋形變，就可以解析出相位，從而重建三維形貌。

第五是大氣和水等混沌介質，這種我們可以稱為“計算介質”的東東，在成像中往往起着很壞的作用，大氣擾動會使天文望遠鏡看不清目標，於是就產生了自適應光學；還會產生散射，我在上一篇裏已有論述。

第六是傅里葉變換。傅里葉變換也是複數形式，有頻譜圖和相位圖；圖像傅里葉變換相位圖代表的是圖像的位置和結構信息。在計算光學成像中，我們經常遇到的是在頻域裏處理信息，就會與傅里葉相位打交道，散斑自相關成像就是典型的案例，其相位恢復就是恢復傅里葉變換相位。傅里葉望遠鏡當然關係更大了。

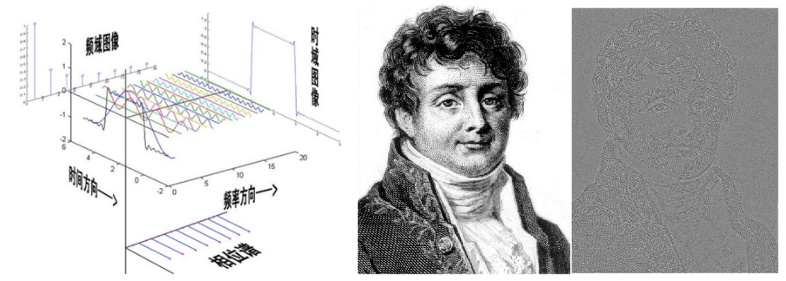數學的傅里葉變換

還有一種是相關運算引入的相位。其實可以把相關運算看作與傅里葉變換是一樣的東西，只是一種拓展而已。

再進一步看，其實還有很多與相位相關的，比如有像差的光學系統、多目相機、微透鏡陣列、多角度照明等，都有相位的引入。只是，這些相位有的是“壞”的，我們不想要的，比如像差，而有的是我們想要引入的“好”的相位，比如多角度照明。

上面説了這麼多，那相位到底能幹什麼？

2 相位能幹什麼？

首先，相位屬於高維度的物理量，高維度的信息經過好的處理，投影到低維度，一定會有好的結果，這當然要看我們在低維度空間到底想要什麼。專欄的第一篇裏已講到，光電成像朝着“更高、更遠、更廣、更小、更強”的目標發展，從應用的維度上看，我們需要把偏振、光譜、相位等高維度的物理信息轉換為分辨率、作用距離、視場、重量體積和環境適應能力等，當然還有深度信息。

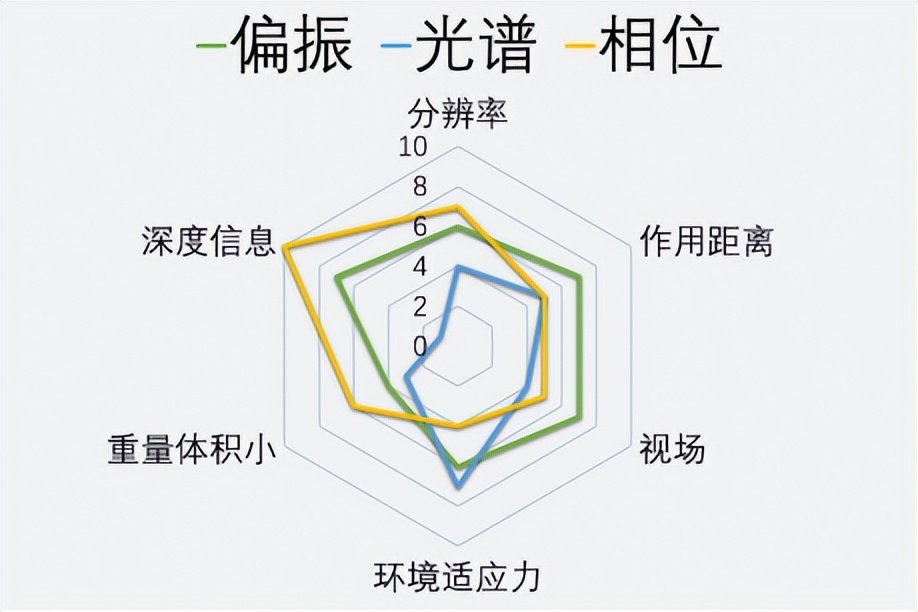維度信息效能雷達圖

下面就討論一下“相位”在計算光學成像中的法力。

從相位本身的物理意義上來看，它是表徵“相對位置”的一個物理量，那就天然地就決定了它具備與位置相關的能力，比如全息就是一個典型的例子。那麼，相位在三維成像、提高成像分辨率、簡化光學系統設計和提高環境適應能力等方面能發揮什麼作用。

· 三維成像方面的相位

全息成像真正拉開了三維成像的序幕，從全息幹板到現在的數字全息，都離不開相位，只是幹板記錄的是干涉條紋，通過光源照射還原相位信息，能看到真實的三維圖像，而且，即使幹板打碎，每一個小塊都記錄了物體的全息圖，只是分辨率下降了；而數字全息則通過光電探測器記錄全息圖，藉由標量衍射理論從干涉強度圖裏恢復出相位，從而達到全息的目的。

光電成像和顯示，一定要走向三維！而光電成像實現的二維圖像，沒有深度信息，就談不上三維。那如果能記錄下或者恢復出相位，可否像全息成像，重建出三維的圖像呢？答案是肯定的。

利用非相干光進行三維的成像的例子有：雙目立體視覺、結構光照明三維成像、偏振三維成像和散射成像等。

雙目立體視覺是利用視差和三角幾何關係實現的，只是深度計算模型按照理想相機建立的，實際應用時，需要對雙目相機進行標定，得到內外參數和相應矩陣。這個應用與相位無關。

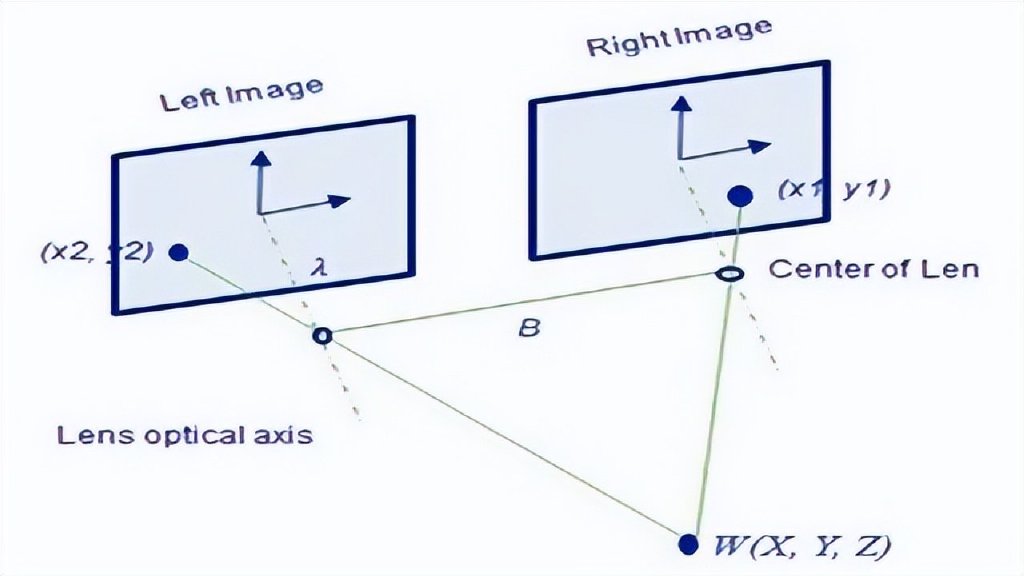
雙目立體視覺

結構光照明三維成像是採用正弦條紋、格雷碼和隨機紋理等編碼圖案的主動照明方式，引入相位信息，當然，我們也可以採用時間編碼方式。以正弦條紋為例，將正弦條紋通過投影設備投影至被測物後會發生彎曲形變，根據彎曲程度可以解調得到相位，再將相位轉化為全場的高度。這就是結構光三維成像的基本原理，其他的編碼形式與此類似。很顯然，這種方法與全息不同，只能對結構光照到的形貌進行三維重建，這意味着只能從一個方向觀測，它是三維的，但不具有“全息”特性。

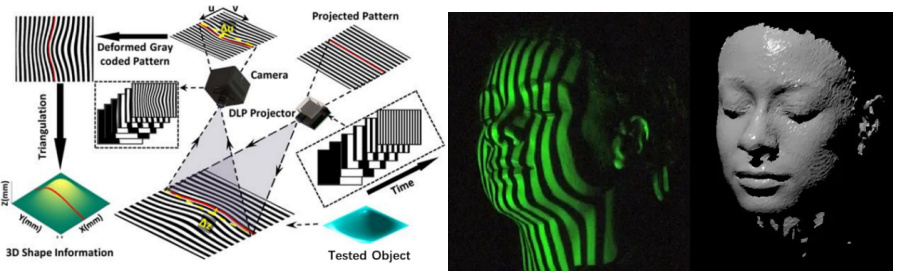基於格雷碼圖案投影的結構光三維成像技術

偏振三維成像本質上利用偏振角信息重建三維形貌，這個偏振角其實也是相位，在第四篇文章已有論述。

我們知道，散射光場具有“全息”特性，一方面，我們可以從散射場中解譯出相位信息，從而獲得景深數據，實現三維重建；另一方面，選取一小塊散斑也能解譯出物體信息，只是分辨率下降了，這與全息很像。其實，我們從另外一個角度看，散射可以認為是一種特殊的結構光編碼形式，既有幅值的調製，也有相位調製。這既是散射成像的魅力，也是挑戰，需要我們更好地去發掘。

· 提高成像分辨率的相位

1953年，荷蘭科學家澤尼克因發明了相襯（Phase Contrast）顯微鏡獲得諾貝爾物理學獎，這是第一個把相位變成強度的成像案例，其原理是利用光的干涉原理，將相位差轉換成振幅差（即明暗差）的顯微鏡裝置。相襯顯微鏡實際上是把人眼看不到的相位信息轉換為強度，可以解決透明物體的成像問題。

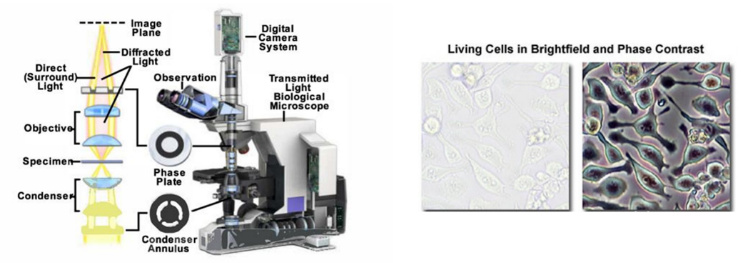相襯顯微鏡與成像結果

那麼能不能利用相位提升分辨率呢？這幾年一直在流行“相位成像”，就是從強度中恢復相位信息，主要兩種手段：一種是相干光照明，根據光的衍射理論，光的相位能影響到強度信息，可以通過在光路中引入某些光學元件使得相位能夠反應在圖像上，記錄下相襯；另外一種是通過已知的強度信息，利用傅里葉光學原理解譯出相位，稱之為定量相位成像（quantitative phase imaging）。

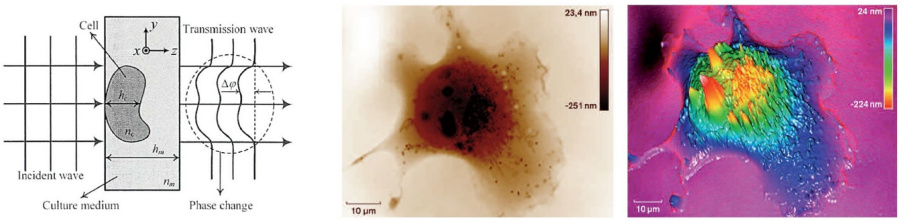相位定量測量原理與細胞的定量相位成像

説起分辨率，就必須要説説阿貝衍射極限，光學成像分辨率可以表示為δ=kλ/NA，其中k為係數，如0.61，λ為波長，NA為數值孔徑。從公式上來看，提升分辨率的手段基本上就是減小波長，提高數值孔徑。很顯然，對大多數成像而言，數值孔徑更重要。提高數值孔徑除了常規的增大光學口徑和油浸介質等手段外，採取的方法都與相干有關，而相干必然離不開相位。常見的結構光照明成像、疊層成像、散射成像和合成孔徑成像，都離不開相位。關於這些內容，我想在之後的文章裏專門討論。

現在我們要思考的是能不能把相位這個高維度的量投影到分辨率這個維度，能否提升分辨率？可以。看一個現實的例子：人的雙目視力是超過單隻眼睛的，原因就是這裏有視差，從而引入了相位，在大腦視覺合成時提升了分辨率。這個是不是很有意思？在這裏，我問一個問題，這個相位是什麼？如何引入的？還有哪些方法，能夠把相位與分辨率緊密結合起來？

· 簡化光學系統設計的相位

光學系統設計的本質是對相位的優化控制，傳統的光學系統為了減小像差採用多片鏡片的組合優化設計，帶來了好的像質也犧牲了體積、重量和加工成本。在計算光學系統設計中，簡化光學系統的核心必然是相位的混疊和解譯。説起來很簡單，在光學系統中減少了鏡片，增加了編碼過程，這都會引入相位的變化；如果把成像看成線性模型，那麼解譯就是求共軛矩陣的過程，使之能夠恢復到傳統光學成像的效果；如果是非線性模型，那就應該考慮減少鏡片和編碼過程引入的相位變化，可否做景深的延拓和分辨率的提升。