我們能聽出鼓的形狀嗎?_風聞
中科院物理所-中科院物理所官方账号-2022-07-28 13:57
原創:中科院物理所
之前我們在每週直播整活環節弄了一期“聲之形”,即看見聲音的形狀,在那裏我們嘗試看見了一維超聲波發生器形成的駐波,也看見了二維金屬板上形成的駐波(即克拉尼圖形)。

超聲波聲懸浮示意圖,圖源網絡

克拉尼圖形,圖源網絡
但無論怎樣,都是先固定了裝置的幾何形狀,再去考慮這個幾何形狀上能夠產生怎樣的聲音(振動),那麼一些腦洞大開的人可能會問:這個問題反過來會怎樣呢?我們能夠通過聲音來判斷髮聲裝置的幾何形狀嗎?
事實上,這個問題有一個更加簡練,更加廣為流傳的版本:我們能聽出鼓的形狀嗎?(Can one hear the shape of a drum?)而這也是數學家Mac Kac 於1966年那篇著名的文章的標題。為了從數學上考慮這個問題,我們必須把問題重新表述一下。
什麼是鼓?
首先,一個鼓面的振動由什麼方程描述?我們可以想象一下,把一個膜拉伸套在一個剛性支架上,這樣就形成了一張二維的鼓。這張二維的鼓的振動是由波動方程描述的,同時因為鼓面的邊緣牢牢地貼在剛性的架子上,我們可以認為波動方程的邊界條件是狄利克雷邊界條件。如果我們用函數F(x,y,t)來描述鼓面處於位置(x,y)處的點在t時刻於z方向的偏移量,那麼鼓面的波動方程就可以寫為,
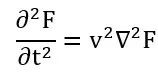
分離變量F=U*exp(iωt),化成本徵值問題
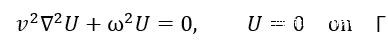
其中U(x,y)是鼓在z方向的偏移量,v是鼓面的波速,在這裏是一個無關緊要的常數。ω是振動頻率,Γ是鼓的邊界。為了簡化我們的記號,我們可以認為我們研究的方程具有如下形式:
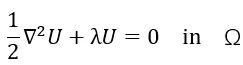
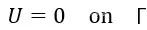
其中Ω表示鼓的內部,λ是拉普拉斯算子的本徵值,與之前提到的鼓的本徵頻率是一一對應的。那麼,數學上 “聽鼓辨形”則可以表達為,如果我們已知某面鼓的所有本徵值,我們能否唯一地確定鼓的形狀Ω和Γ。

所以數學家提出的問題是,如果我們知道了一張鼓的所有振動頻率,我們能唯一地確定鼓的形狀嗎?
鼓的面積
在揭曉答案之前,讓我們將目光放在Kac
1966年的文章中,去看看一些物理上的直覺能夠給我們帶來哪些有意思的結果?正如Kac在他的文章裏提到的那樣,類似拉普拉斯算子在某個區域內的本徵值問題最早可以追溯到Weyl那個年代,如果我們給定一個λ,考慮本徵值小於λ的個數,即考慮函數
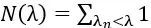
Weyl證明了當λ→∞時,
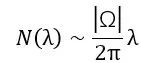
**這意味着如果我們知道了鼓的所有本徵頻率,我們至少可以知道鼓的面積。**讓我們稍微仔細觀察一下Weyl得到的結果,拉普拉斯算子在一個鼓上的本徵值的分佈,當本徵值很大時,分佈在區間[λ,λ+dλ]內的本徵值的個數正比於鼓的面積,而與λ無關,與鼓的形狀也無關。
接下來,我將展示我們可以用一種物理類比來“論證”Weyl證明的定理。首先,我想強調一點,數學上“聽鼓辨形”問題其實是拉普拉斯算子在一個區域內的本徵值問題,它不僅僅出現在波動方程中,還出現在量子力學裏的Schrödinger方程以及擴散方程中。在這些不同的物理問題中,擴散問題最容易為我們提供關於拉普拉斯算子本徵值分佈的物理直覺,因而我們這裏想重點展示一下如何從擴散方程中汲取靈感來得到“聽鼓辨形”問題的部分答案。
首先,擴散方程是描述擴散現象的偏微分方程,而擴散現象大致就是在説,隨着時間的推移,物質會自發地從濃度高的地方往濃度低的地方進行擴散,如果我們用函數
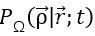
來描述物質在時刻t,位置r處的濃度,那麼這個函數將滿足擴散方程:
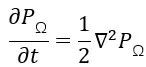
並有邊界條件
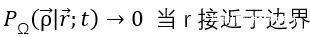
以及初始條件
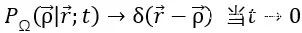
通過分離變量我們可以得到我們熟悉的本徵值問題
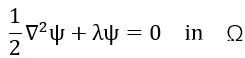
以及
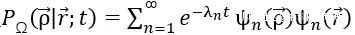
現在,從直觀上講,對於非常小的時間t,擴散物質的粒子沒有足夠的時間來感受邊界Γ的影響。因此,我們期望有
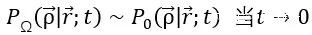
其中

仍然滿足相同的擴散方程以及相同的初始條件,但這次沒有其他條件的限制(如邊界條件的限制),唯一需要滿足的就是物質的濃度需要處處大於等於0,即P₀≥0。
在這種情況下,關於P₀的顯示錶達式就是著名的高斯分佈,
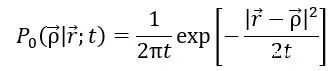
故而根據我們在上面的論斷,當t→0時,應當有
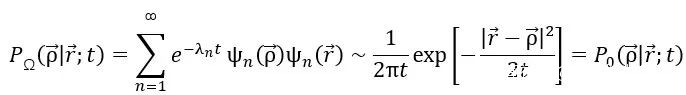
如果這個公式在位置r=ρ處也是正確的話,我們就可以得到
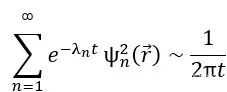
如果我們更進一步,對上式兩邊進行積分,利用歸一化條件
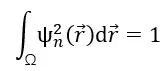
可得
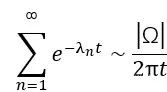
注意到上式還可以寫成如下形式,
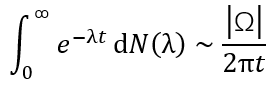
其中
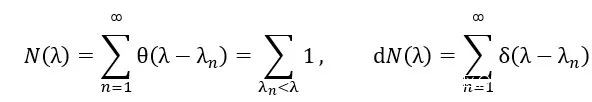
那麼這個時候如果我們應用Hardy-Littlewood Karamata Tauberian 定理(這個定理的內容將在文末進行説明),我們就可以得到
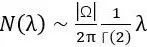
而這正是Weyl的結果(Γ(2)=1)。
以上只是基於物理的類比給出的並不嚴格的論證,當然我們可以用數學語言將上面的這些論述嚴格化,但這超出了本文的目標,感興趣的讀者可以直接閲讀Kac的原文。總之,我們現在至少可以確認我們能夠聽出鼓的面積。
其他信息呢
但我們能夠聽出更多的信息嗎?事實上,我們可以利用同樣的類比繼續考慮這件事情,假設在擴散問題中,物質一開始集中的地方非常靠近邊界,即我們的初始條件裏的ρ非常靠近區域的邊界,那麼此時在開始非常短的時間t內,一條直線構成的邊界條件應當是非常好的近似(如下方左圖所示),
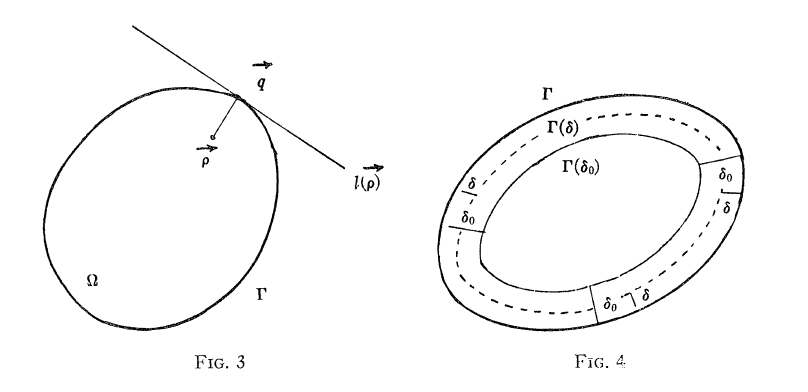
於是我們可以得到,
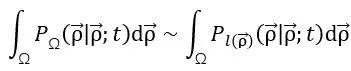
其中Pl(ρ)是l(ρ)以直線作為邊界條件得到的解,而
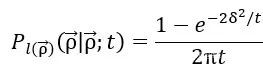
其中δ是ρ到邊界Γ的最短距離。對於積分而言,上式中指數衰減那一項將只有非常靠近邊界的區域才會有所貢獻,稍加計算,可以得到如下公式,
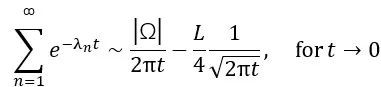
右邊第一項是我們一開始得到的結果,而指數衰減那一項能夠告訴我們邊界的周長信息,也就是説,我們可以聽出鼓的周長!
我們還能聽出更多的東西嗎?事實上,對於凸多邊形鼓,Kac得到了如下公式,
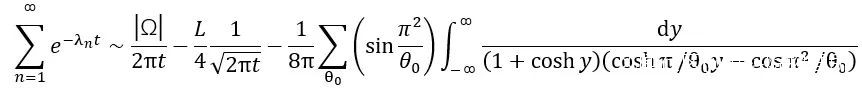
其中θ₀是多邊形的每一個角度。如果這個多邊形有N條邊,並且如果我們讓N→∞使得每一個θ₀→π,那麼上式的常數項將變成
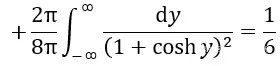
這似乎在説光滑的鼓給出的常數項都是一樣的,我們沒法通過常數項對鼓進行區分。復連通的鼓會怎樣呢?如果我們讓所有多邊形都接近平滑曲線,結果是常數項將變成(1-r)1/6,其中r是鼓面上洞的個數。因此,可以很自然地推測,對於具有r個光滑洞的光滑鼓,我們有
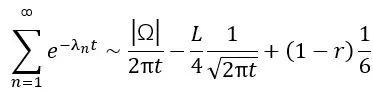
也就是説我們還可以聽出鼓的拓撲(即鼓面洞的個數)!
以上便是Kac 1966年的文章裏的主要結論了,在這篇文章中Kac也表明他還不清楚“聽鼓辨形”的終極答案。直到1992年,Carolyn Gordon、David Webb和Scott Wolpert根據Sunada方法在平面上構造了一對形狀不同但特徵值相同的區域。這些區域是凹多邊形。兩個區域具有相同特徵值的證明使用了拉普拉斯算子的對稱性。Buser等人對這一思想進行了推廣,他們構建了許多類似的例子。因此,Kac問題的答案是:對於許多形狀,人們無法完全聽出鼓的形狀。然而,正如Kac最初的文章那樣,我們可以推斷出一些鼓的信息。
另一方面,Steve Zelditch證明了,如果對具有解析邊界的某些凸平面區域施加限制,則Kac問題的答案是肯定的。

Gordon、Webb、Wolpert構造的反例,兩個不同形狀的鼓具有完全相同的本徵頻率。注意到這兩個鼓具有相同的面積和周長。[3]
在實際中,**由於鼓的音色是由本徵振動模式的相對振幅集決定的,因此僅僅擁有一組完全相同的本徵頻率並不足以讓兩個鼓聽起來相同。**對於每個本徵模,它們還需要具有相同的相對振幅,這在實際中可能並不容易實現。
此外,人們無法直接聽到鼓(鼓膜)的振動。相反,我們的耳朵聽的是空氣中聲波的振動,所以我們還需要考慮聲音的傳播……這將變得更加複雜。因此,在實際生活中,似乎很難找到兩個聲音相同的不同鼓。
數學補充
Hardy-Littlewood Karamata Tauberian 定理,當y→0+時,數列an以下的兩個漸進行為將是等價的,
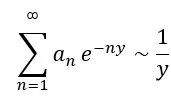
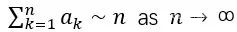
Feller推導出關於這個定理的更一般的形式,考慮有界變差的實值函數
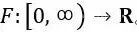
(這裏,僅局部需要有界變差:即在[0,∞)上的每個有界子區間上滿足有界變差即可。然而,此時需要對變換的收斂性進行更復雜的附加假設。)定義:
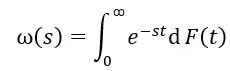
該定理以以下方式將ω的漸近性與F的漸近性聯繫起來。如果ρ是非負實數,則以下陳述是等價的。
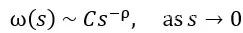
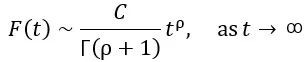
參考資料:
[1] Kac, M. (1966). Can One Hear the Shape of a Drum? The American Mathematical Monthly, 73(4), 1–23. https://doi.org/10.2307/2313748
[2] Can We Hear the Shape of a Drum? | COMSOL Blog
[3] Hearing the shape of a drum - Wikipedia
[4] Hardy–Littlewood Tauberian theorem - Wikipedia