16個數論難題，你能看懂多少？解決多少？| 袁嵐峯_風聞

導言：

大家應該瞭解這些有趣的數學問題，同時更應該瞭解這背後的數學思想、研究範式。如果你能為數學範式的進步做出貢獻，你就會成為偉大的數學家。

你想成為數學大佬嗎？我有些朋友非常熱心數學科普，組織了一個“哆嗒數學網”。最近，哆嗒數學網發了一篇簡短的文章《15個數論難題，解決任意一個都能讓你稱為頂級大佬 | 哆嗒數學網）。下面我來結合自己的理解，更詳細地介紹一下。讓我們來看看，這15個問題你能解決多少，或者能看懂多少。對我來説很明確：全都能看懂，一個都解決不了。（下面要多次用到乘方符號，而有些編輯器顯示不出上標，因此用x^y表示x的y次方。）

第一個問題是鼎鼎大名的哥德巴赫猜想（Goldbach conjecture）：每個大於等於4的偶數都可以表示成兩個質數之和。這也就是陳景潤一心想證明的1 + 1——請注意是1 + 1，不是1 + 1 = 2！1 + 1 = 2是個小學知識，完全不需要證明。經常有些人納悶，陳景潤為什麼要證明1 + 1 = 2，難道數學家吃飽了撐得沒事幹嗎？難道1 + 1 = 2很高深嗎？其實這完全是誤解。

哥德巴赫猜想

哥德巴赫猜想中的1 + 1是個簡稱，這裏的1是表示只有一個質因數的整數即質數。1 + 1的意思就是任何一個足夠大的偶數都可以分解成兩個質數之和，即哥德巴赫猜想。由於這個猜想太難啃，人們先嚐試去攻克它的較弱版本，如9 + 9、1 + 3等等，陳景潤證明的是1 + 2。這裏的2表示質因數數目不超過2的數，即它或者是質數，或者是兩個質數的乘積。類似的，3表示質因數數目不超過3的數，9表示質因數數目不超過9的數，如此等等。

瞭解了這些記法，你才能明白陳景潤的1 + 2是什麼意思。它説的是，任何一個足夠大的偶數都可以分解為一個質數加上一個質因數數目不超過2的數（陳景潤究竟為證明哥德巴赫猜想做出了哪些貢獻？| 科學大院）。在陳景潤之前，人們先是證明了9 + 9，然後是7 + 7、6 + 6、3 + 4、1 + 5、1 + 4、1 + 3等等。陳景潤取得了這個方向上迄今為止最強的結果1 + 2，這是一個偉大的成就。這看起來離哥德巴赫猜想只有一步之遙，但這一步極其困難，到現在人們還沒跨過去。

陳景潤

第二個問題是考拉茲猜想（Collatz conjecture），或者稱為角谷猜想、冰雹猜想、421猜想、3x + 1猜想等等。最後這個名字，3x + 1猜想，會讓人很快明白它説的是什麼。取一個正整數x，如果它是偶數，就把它除以2，如果它是奇數，就把它乘以3再加上1，即變成3x + 1。然後按照同樣的規則，把這個操作無限進行下去。這個猜想説的是：無論你最初取的x等於多少，最終都會進入4-2-1-4-2-1的循環。稍微想一下就會明白，進入這個循環就出不來了，因為4的下一步是2，2的下一步是1，1的下一步又回到了4。但問題在於，是否一定會進入這個循環呢？

 

從100出發的3x + 1猜想序列

你可以拿幾個數試驗一下，你會發現都是如此。有些很快就進入循環，有些要很久才進入循環，但或早或晚都會變成4-2-1-4-2-1。數學家已經用計算機驗證到了2^68 ≈ 2.95 × 10^20，都滿足這個規律。然而計算機只能驗證有限，不能證明無限。這是不是對所有的自然數都成立？目前還完全不清楚！

第三個問題是勒讓德猜想（Legendre’s conjecture）：對任意一個自然數n，在n^2和(n + 1)^2之間都至少存在一個質數p。按照我對這個領域的一點點了解，在這個方向上最重要的結果是伯特蘭-切比雪夫定理：對任何大於3的自然數n，都至少存在一個質數p滿足n < p < 2n - 2。勒讓德猜想看起來只是伯特蘭-切比雪夫定理的一個改進，但這個改進到現在都沒得到證明。

勒讓德（Adrien-Marie Legendre，1752 - 1833）

第四個問題是鼎鼎大名的孿生質數猜想（twin prime conjecture）：存在無窮多對質數，它們之間只相差2。這樣的一對質數，叫做孿生質數。我以前介紹過，中國數學家張益唐在這個問題上取得了突破性進展（質數的最小間隔有上限，人的奮鬥沒有上限 | 袁嵐峯）。他證明了，存在無窮多對質數，它們之間的差距不超過7千萬。假如把7千萬縮小到2，就證明了孿生質數猜想，但現在還沒有做到。

張益唐

如果你沒有理解這為什麼是個突破，我們來稍微解釋一下。7千萬雖然看起來是個很大的數，但以前是完全不能肯定有這樣的上限存在。所以張益唐是從無限進步到了7千萬，這是質的區別，而從7千萬到2只是有限到有限，這是量的區別。目前的最好結果，是把這個差距縮小到了246。但再往下就十分困難了，還需要新的思想。

第五個問題是梅森質數猜想。梅森（Marin Mersenne, 1588－1648）是十七世紀的法國數學家，他研究了2^p - 1類型的數，其中p是一個質數。現在我們把這樣的數叫做梅森數，記為Mp。假如對於某個p，Mp是個質數，就把它稱為梅森質數。梅森質數猜想説的就是：存在無窮多個梅森質數。

梅森

是不是真的這樣呢？沒人知道。我們知道的是，尋找梅森質數是目前尋找大質數最好的辦法。近幾十年來找到的最大的質數，都是通過對梅森質數的搜索找到的。例如2018年發現了目前最大的梅森質數也就是目前最大的質數2^82589933 - 1，它是個24862048位數。

第六個問題是n^2 + 1猜想：存在無窮多個自然數n，使得n^2+1是質數。這個猜想的表述出奇的簡單，證明卻完全無從下手。

第七個問題是費馬數猜想。這個猜想的風格跟前面的正好相反，前面那些都是要證明有無窮多個什麼什麼，這個卻是要證明某個東西只有有限多。是什麼東西呢？是説費馬數中的質數只有有限多。什麼叫費馬數？就是那些形如2^(2^n) + 1的數，其中n = 0，1，2，3，4……我們把它記為F(n)。

費馬（Pierre de Fermat，1601 - 1665）發現，當n從0到4時，F(n)都是質數。大家可以來檢驗一下，這五個數分別是3、5、17、257和65537，確實都是質數。下一個F(5)太大了，費馬沒有去檢驗，他就興致勃勃地猜想費馬數全都是質數。結果將近一百年後，歐拉發現F(5)是個合數，它等於641 × 6700417，這就推翻了費馬的猜想。更令人大跌眼鏡的是，後來人們算出的費馬數全都是合數，再也沒見到一個質數！所以現在我們的猜想反過來了，變成了費馬數中只有有限個質數。更進一步，説不定費馬數中的質數只有最初的那五個呢，誰知道？

費馬

第八個問題是奇完全數猜想。所謂完全數（perfect number）或者完滿數、完美數就是這樣的自然數，它的所有真因數之和等於它自己。請注意這裏説的是真因數而不是質因數，真因數就是那些小於它自己的因數。例如6是一個完全數，因為6的真因數只有1、2、3，而1 + 2 + 3剛好等於6。又如28的所有真因數是1、2、4、7、14，這些數加起來等於28，所以28也是完全數。

 

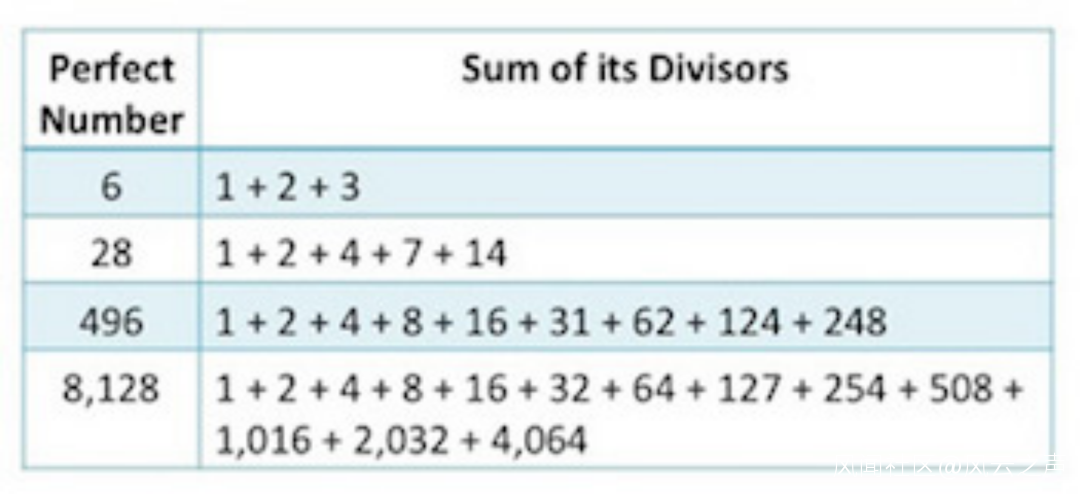
完全數

截止2018年，已經找到了51個完全數。它們全都是偶數，而且全都可以表示成Mp (Mp + 1)，這裏的Mp是前面剛剛介紹過的梅森質數。所以奇完全數猜想就是問：是否存在奇的完全數？目前完全不清楚。目前我們知道的是，假如存在奇的完全數，那麼它必須要大於10^1500。

第九個問題是完美長方體猜想。所謂完美長方體（perfect cuboid）就是這樣的長方體，它的長、寬、高和所有的對角線（包括面對角線和體對角線）的長度都是整數。也就是説，它的長寬高a、b、c是三個自然數，而且a^2 + b^2、a^2 + c^2、b^2 + c^2以及a^2 + b^2 + c^2都是平方數。完美長方體猜想就是問，是否存在這樣的一組自然數？ 

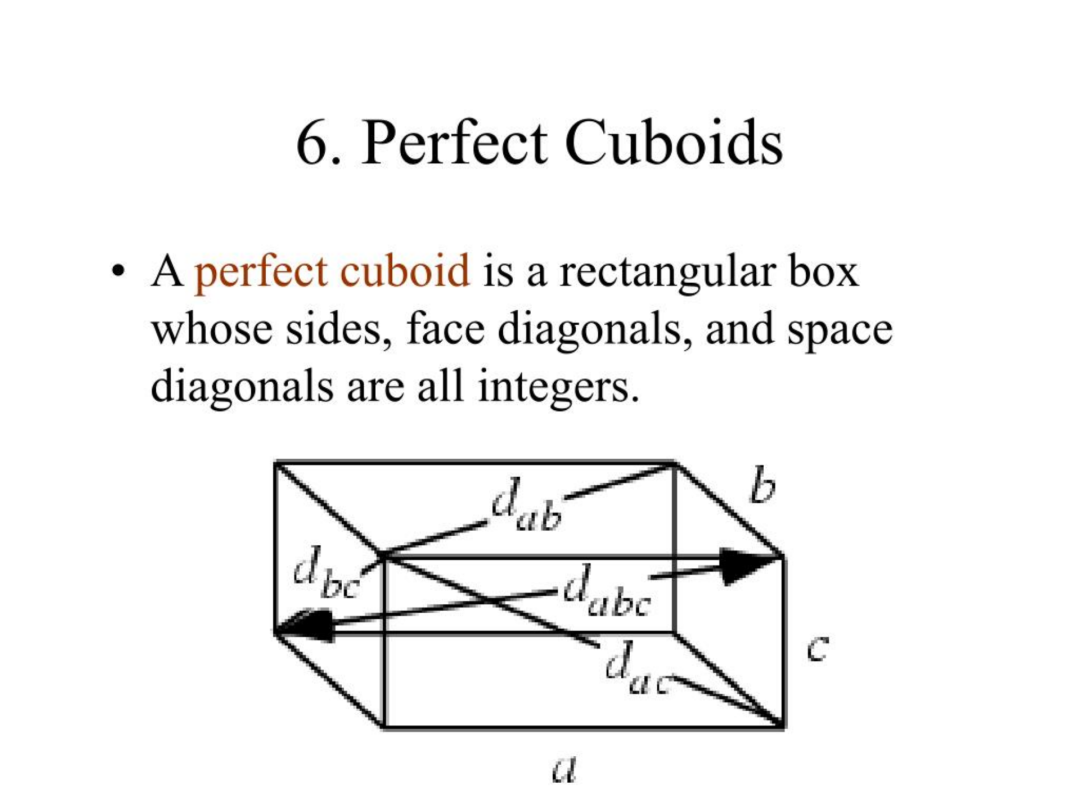
完美長方體

我看到這個問題時大為吃驚，因為我知道兩個平方數相加在什麼情況下是平方數是個早已解決的問題，也就是所謂勾股數：a = p^2 - q^2，b = 2pq，c = p^2 + q^2，其中p和q是兩個任意的自然數。但三個平方數相加在什麼情況下是平方數，居然直到現在都沒有解決！由此導致，完美長方體是否存在，現在沒人能證明或證偽。數值驗證的結果是，假如完美長方體存在，那麼它最小的奇數稜長不小於2.5 × 10^13（https://unsolvedproblems.org/S58.pdf）。

第十個問題是鼎鼎大名的黎曼猜想（Riemann hypothesis）。我絲毫不打算用簡單的語言來解釋這個問題，因為——完全不可能。我以前做過一系列節目，來完整地介紹黎曼猜想（黎曼猜想（六）1859年就提出的黎曼猜想，數學家證明到什麼程度了？| 科技袁人）。在這裏只能告訴大家，這個猜想説的是：黎曼ζ函數的所有非平凡零點的實部都等於1/2。

 

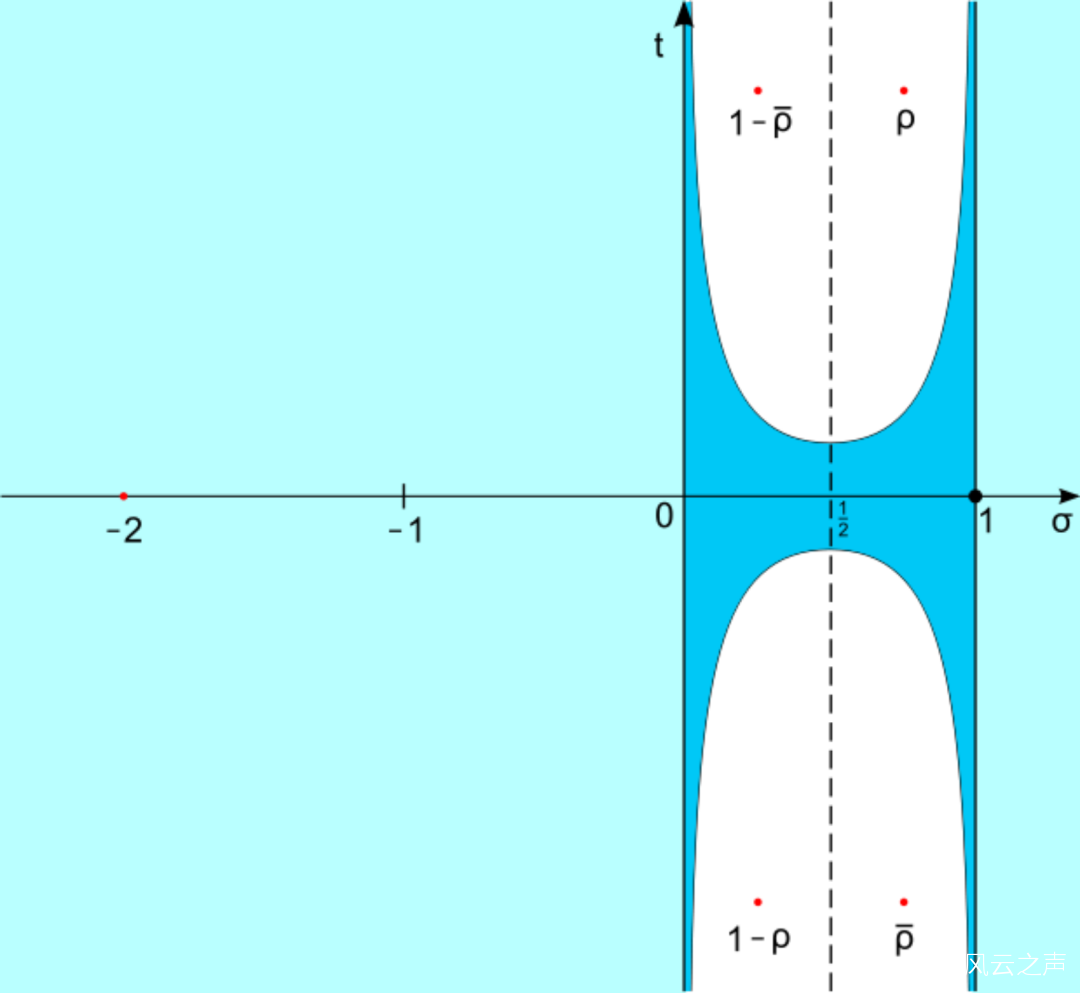
用複平面表示黎曼猜想：黎曼ζ函數的所有非平凡零點都在實部等於1/2的臨界線上

這説的是啥？確實，要理解這句話裏的每個詞是什麼意思都非常不容易，需要複變函數的知識。如果你聽不懂黎曼猜想説的是什麼，沒關係，只要知道它是整個數學界最重要、最著名的那“一個”未解之謎就行了。

第十一個問題是關於歐拉-馬歇羅尼常數（Euler-Mascheroni constant）的。這個常數的來源是：歐拉證明了，所有自然數的倒數和，即1 + 1/2 + 1/3 + … + 1/n，是發散的，而它發散的速度是lnn。也就是説，1 + 1/2 + 1/3 + … + 1/n - lnn在n趨於無窮的時候會趨於一個極限，這個極限現在稱為歐拉-馬歇羅尼常數。馬歇羅尼（Lorenzo Mascheroni，1750 - 1800）是一位意大利數學家，他把這個常數記為γ，並把它算到了小數點後32位，但後來發現他在第20位出現了錯誤。無論如何，馬歇羅尼通過對這個常數的研究把自己的名字刻在了數學史上。

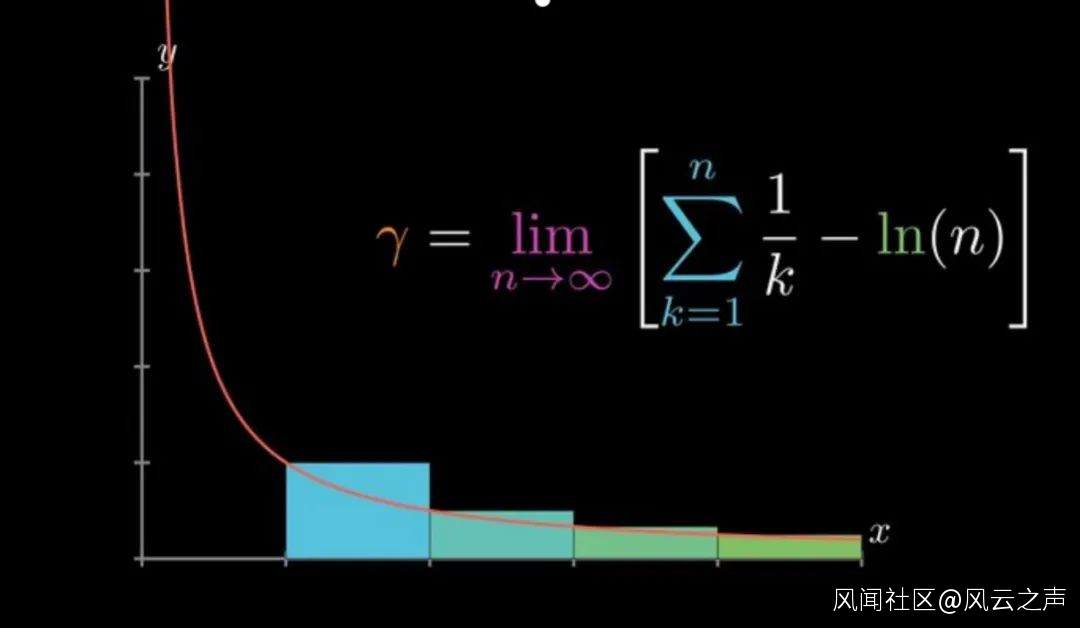
歐拉-馬歇羅尼常數

現在我們知道，γ約等於0.57721。但問題是，它是一個有理數還是無理數？這麼基礎的問題，我們居然不知道答案！在直覺上，它是無理數的概率顯然比它是有理數的概率大得多——但目前完全無法證明。

我來補充一點，其實數學裏還有很多類似的問題。例如兩個極其常見的數圓周率π和自然對數的底e都早已證明了是無理數，但π + e是不是無理數？目前就沒人知道！

第十二個問題是關於黎曼ζ函數的：當k為正奇數時，ζ(k)是否為超越數？前面説了，明白黎曼ζ函數是什麼需要複變函數的知識。不過這個函數對於正實數的自變量卻很容易理解，如果把自變量寫成s，ζ(s)就是所有自然數的s次方的倒數和，即

ζ(s) = 1 + 1/2^s + 1/3^s + 1/4^s + …

你也許還想問，什麼叫超越數？超越數就是那些不能表示成整係數多項式方程的解的數，它是無理數的一個真子集。例如根號2是無理數，但它不是超越數，因為它是整係數多項式方程x^2 - 2 = 0的解。而π已經證明了是超越數，由此得到一個重大結果：經典尺規作圖問題“化圓為方”無解，因為你不可能通過有限次操作得到根號π。 

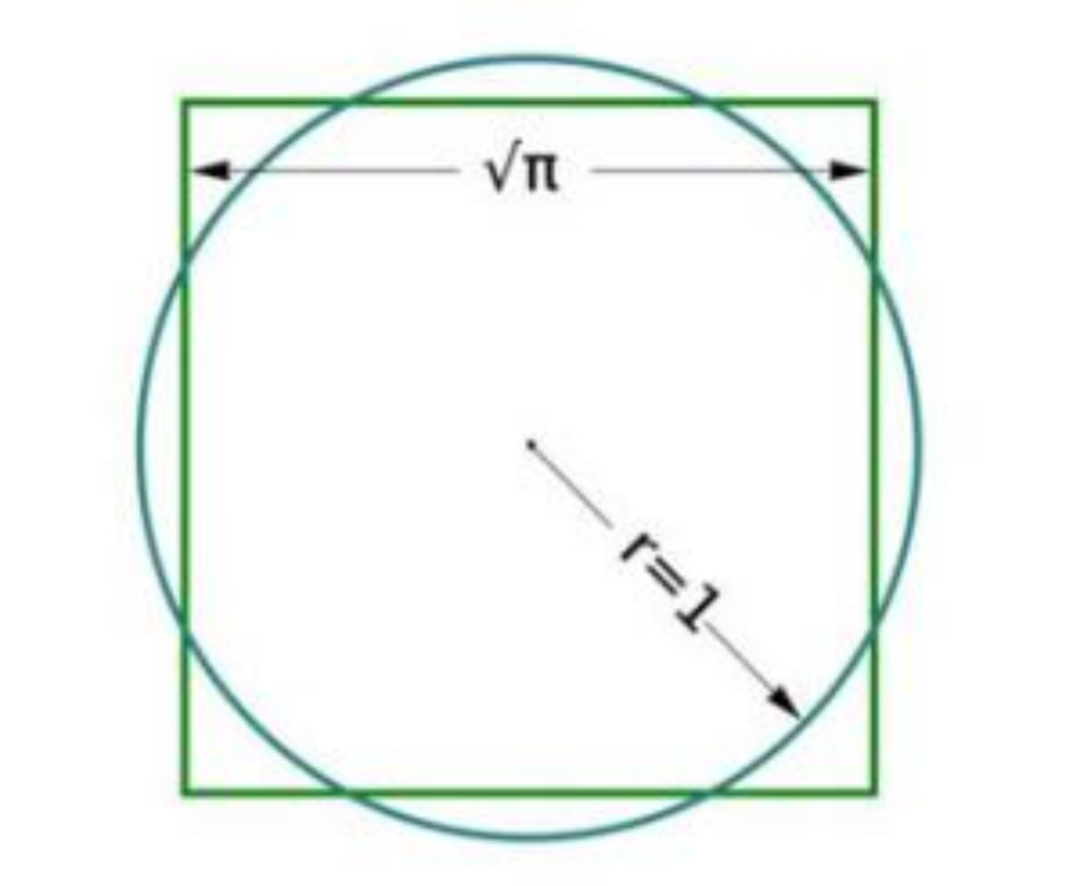
化圓為方

回到黎曼猜想。當k為正偶數時，已經證明了ζ(k)必然是超越數。所以對於正奇數的k，ζ(k)是不是超越數就成為一個有趣的問題了，目前還不知道答案。

第十三個問題是埃爾德什倒數和猜想。這個猜想的表述十分奇妙：如果A是一個正整數的無窮子集，而且A中所有數的倒數和發散，那麼A包含任意長度的等差數列。前面我們説了，所有自然數的倒數和是發散的，所以會有它的子集也滿足倒數和發散。但為什麼這會導致A包含任意長度的等差數列，我就完全沒看出來！埃爾德什的思路真是天馬行空！一個有趣的特例是所有質數的集合，格林和陶哲軒證明了所有質數的倒數和發散，而且所有質數中包含任意長度的等差數列。這個成果幫助陶哲軒得到菲爾茲獎。

1985年，10歲的陶哲軒和埃爾德什在一起

第十四個問題是拉姆塞數（Ramsey number）。什麼叫拉姆塞數？大家可以看我的科普書《量子信息簡話》，在第五章第四節的選讀內容中，就介紹了拉姆塞理論。

《量子信息簡話》

拉姆塞理論説的是：給定足夠多的樣本，那麼任何複雜的結構都會必然出現。例如有一個著名的定理：6個人中必然有3個人互相認識或者3個人互相不認識。換一種説法就是，6個點之間兩兩連線，每條線都是紅色或藍色，那麼必然會出現一個紅色三角形或者一個藍色三角形。這個定理用拉姆塞理論的語言説，就是R(3, 3) = 6。給定兩個自然數s和t，拉姆塞數R(s, t)的意思是：達到這麼多人，其中就必然有s個人互相認識或者t個人互相不認識。拉姆塞證明了，這樣的數必然存在。

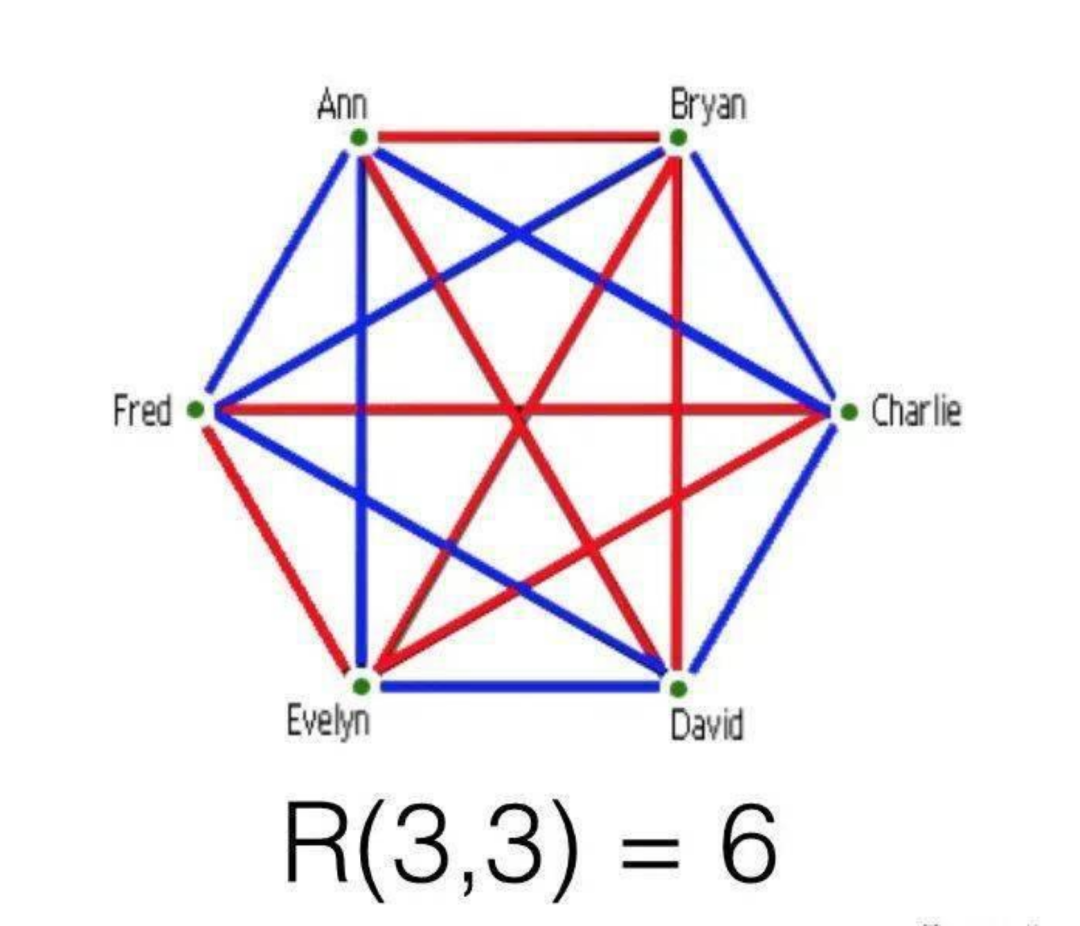
6個人中必然有3個人互相認識或者3個人互相不認識

然而，確定拉姆塞數的難度上升得極快。目前我們知道R(1, 1) = 1， R(2, 2) = 2，R(3, 3) = 6，R(4, 4) = 18，但再往上我們就不知道了。對於R(5, 5)，我們已經可以確定它在43到48之間，但具體是多少仍然不知道。對於更大的n，就更是一頭霧水。所以為了表現拉姆塞問題的難度，埃爾德什有一段著名的論述：

設想有一支外星人的軍隊，比我們強大得多，降落到地球上，要求我們給出R(5, 5)的值，否則就摧毀地球。在這種情況下，我們應該調集我們所有的計算機和數學家，嘗試找到這個值。但假如外星人要求的是R(6, 6)，那麼我們最好的選擇就是嘗試攻擊外星人。

第十五個即最後一個問題，是華林問題（Waring’s problem）。華林問題是一類經典的數論問題，楊振寧的父親楊武之的博士論文就是這方面的研究，這是中國人第一次因為對數論的研究獲得博士學位。

 

楊武之

英國數學家華林（Edward Waring，1736 - 1798）發現，每一個自然數都可以表示成最多9個立方數之和，也可以表示成最多19個四次方數之和。於是他問，是不是對任何一個大於1的自然數k，都存在某個數g(k)，使得任何自然數都可以表示成不超過g(k)個k次方數之和？

華林

希爾伯特（David Hilbert，1862 - 1943）給出了肯定的回答：是的，對於任意一個k，都存在相應的g(k)。但他只是證明了g(k)的存在性，如何把g(k)用k表示出來還不清楚。後來數學家們找到了一個g(k)的表達式，唯一的問題是……它其實不是一個表達式，而是三個表達式，分別對應三種可能的情況。然後，許多數學家猜測這三種情況中只有第一種會發生，那麼答案就會簡化到只剩第一個表達式。

華林問題的解（見維基百科）

其實現在的表達式對於編程序做計算來説已經相當簡單，分三種情況沒什麼大不了的，只是在數學的美感上稍有不足。因此，華林問題究竟解決了沒有？這取決於你怎麼定義解決。用網絡語言可以説，解決了，但沒完全解決。

介紹完了哆嗒數學網總結的這十五個數論難題，我還想補充一個：ABC猜想（ABC猜想證明了嗎？外行看不懂證明，但能瞭解科研的基本經驗 | 袁嵐峯）。這個猜想説的是：如果有兩個互質的自然數a和b，它們的和a + b = c，那麼在絕大多數情況下，abc的根積rad(abc) > c。

很抱歉，這個猜想的表述拖泥帶水，不像前面講的大多數問題那樣簡單明瞭。在這裏可以稍微解釋一下，所謂根積（radical）就是先把一個自然數分解成所有質因數的乘積，然後把所有的質因數相乘一次，無論這個質因數出現了多少次。例如10 = 2 × 5，它的根積就是2 × 5 = 10。而12 = 2 × 2 × 3，它的根積就是2 × 3 = 6。現在大家可以明白，rad(abc) > c是什麼意思了吧？但這個猜想還有一個非常討厭的地方，它説的不是一定如此，而是“在絕大多數情況下”。為什麼會這樣，以及如何精確地表示“絕大多數情況”，歡迎大家看我2020年的介紹文章。

基本上，ABC猜想是一個威力十分強大的猜想。例如有了它就能快速地證明費馬大定理，雖然這是個很粗略的證明，因為還需要一些其他的假設。

用ABC猜想證明費馬大定理

但奇妙的不止是它還沒有被證明，更奇妙的是，有一位日本數學家望月新一號稱證明了它。是的，跟柯南君工藤新一同名。

望月新一

這位新一君為了證明ABC猜想，提出了一整套理論，叫做“宇宙際Teichmüller理論”。

宇宙際Teichmüller理論

這名字聽着嚇死人，但更嚇人的是他自創了很多術語，例如“霍奇劇院”（Hodge theatre）。你沒聽錯，一個數學概念叫做劇院。新一對它的定義如下。

霍奇劇院的定義

呃……如果説有一種美德叫做“用户友好”，那麼新一顯然對此完全沒有考慮！不過這些都是細節，最重要的問題是：他對ABC猜想的證明到底對不對？我沒法看懂他的論文，不過根據我瞭解的信息，除了他和他京都大學的同事之外，基本沒人相信他真的證明了ABC猜想。所以數學界有個笑談，ABC猜想在京都大學成了定理，但在此之外仍然是猜想。

有些數學家認真研究瞭望月新一的論文，指出了其中的一些錯誤。新一做了相應的修正，宣稱這些錯誤已經補上了。但有些數學家認為，有些錯誤仍然沒有得到彌補，而新一認為自己的證明沒錯，是這些數學家沒看懂。於是雙方鬧僵了，這個爭論現在都沒解決。在大多數數學家看來，情況可能就成了“這論文這麼不友好，不值得為它去花費時間”。

最後，我來談談我對大家研究這些數學難題的推薦。基本的建議就是：完全不推薦。因為這些問題都經過長期的研究，許多一流的數學家為它們殫精竭慮，卻都沒有解決。這啓發我們，要解決這些問題，可能需要引進更高明的研究範式。

例如我的朋友、著名數學科普作家沙國祥老師寫過一篇文章《突破研究範式，證明費馬大定理｜沙國祥），介紹了費馬大定理的研究過程。這個經典難題在久攻不克之後，1847年，庫默爾帶來第一次重大突破，引入了代數數論的研究範式。1983年，法爾廷斯帶來第二次重大突破，把費馬大定理跟莫德爾猜想聯繫起來，引入了代數幾何的研究範式。1986年，美國數學家裏貝特等證明費馬大定理是谷山——志村——韋伊猜想的推論，即只要證明了後者，就可以推出前者。谷山——志村——韋伊猜想試圖建立橢圓曲線與模形式之間的聯繫，最終懷爾斯（Andrew Wiles）在1994年證明了這個猜想，為費馬大定理的證明畫上了句號。

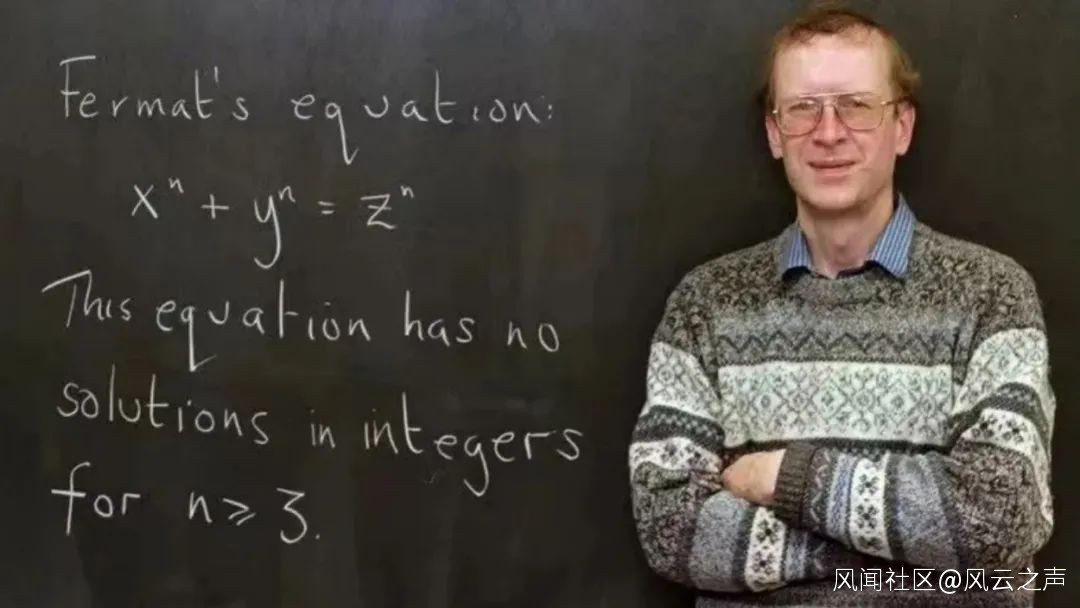
懷爾斯與費馬大定理

因此，沙國祥此文最重要的教益是：“對於非常規數學難題的求解，研究範式的改變，往往起到化難為易、別開生面的效果；如果一味在原有範式裏埋頭苦幹，可能會勞而無功或無本質性進展。反過來，這類問題的探究求解，有時也促進了新範式的建立。”

換一個對普通人來説更容易理解的表述：想用初等方法證明哥德巴赫猜想，就好比騎自行車上月球，是完全不現實的。因此，大家應該瞭解這些有趣的數學問題，同時更應該瞭解這背後的數學思想、研究範式。如果你能為數學範式的進步做出貢獻，你就會成為偉大的數學家。