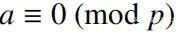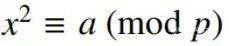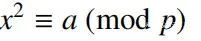如果宇宙的答案是42，那麼問題是什麼？ | 姬揚_風聞

導言：

難道這就是宇宙的終極問題嗎？是還是不是，這是一個問題。

“老實説，我認為問題在於，你從來都不知道問題是什麼。”

這是《美國科學院院刊》（PNAS）的一篇數學論文的開場白。這篇文章的作者是兩位數學家布克爾（Andrew R. Booker）和薩瑟蘭（Andrew V. Sutherland），分別來自於英國的布里斯托大學和美國的麻省理工學院，他們討論的問題是某個丟番圖方程（具有整數解的不定方程）。更準確地説，他們發現了代數不定方程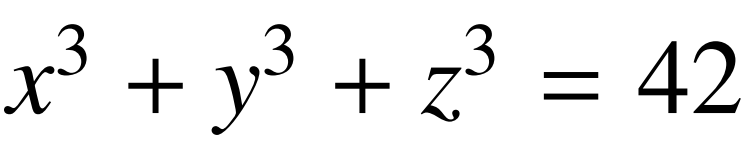的整數解(x,y,z)，其中最小的數也大於1億億，也就是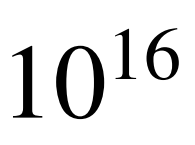，1後面跟16個0。

其實，開場白的這句話不是這兩位數學家説的，而是來自於亞當斯（Douglas Adams）的著名科幻小説《銀河系漫遊指南》，一台超級計算機經過700萬年的思考，得出了關於“生命、宇宙和萬事萬物終極問題”的答案—— 42。這本小説裏並沒有具體地描述這個問題，所以，問題來了：如果宇宙的答案是42，那麼問題是什麼呢？布克爾和薩瑟蘭給出了他們的回答。

薩瑟蘭（Andrew V. Sutherland，左）和 布克爾（Andrew R. Booker，右）

看到這個方程，很多人都會想到費馬大定理（在1637年左右，法國數學家費馬在閲讀丟番圖《算術》的拉丁文譯本時提出的一個猜想）：對於任何大於2的整數n，沒有任何正整數(x,y,z)能夠滿足。

顯然，n=3只是一種特殊的情況，而且著名數學家歐拉早在1753年就證明了它。至於n是大於2的任何整數的情況，則是在1995年被英國數學家懷爾斯（Andrew Wiles）證明了。

既然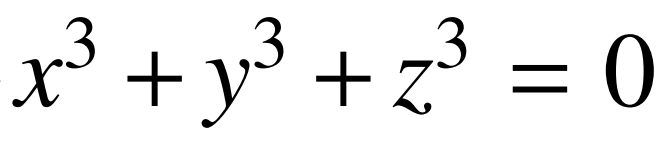沒有整數解，自然就會問，對於什麼樣的整數k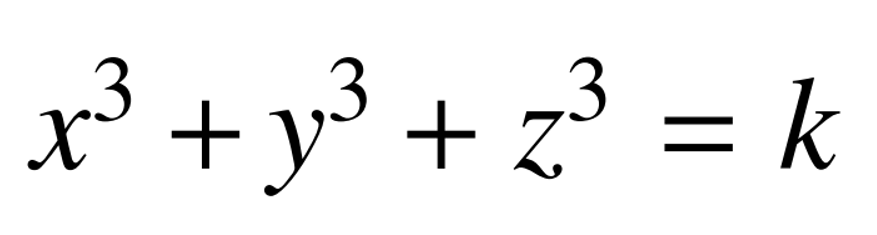，有整數解呢？因為一個整數的立方除以9的餘數只能是0、1或者8，很容易證明，如果k除以9的餘數是4或者5，這個方程就不可能有整數解。但是對於其他的k，仍然有很多方程不知道有沒有整數解。即使在4年以前的2018年，對於小於100的k來説，33和42對應的方程仍然沒人知道有沒有整數解——直到布克爾開始思考這個問題。

2019年，布克爾發表了一篇文章，解決了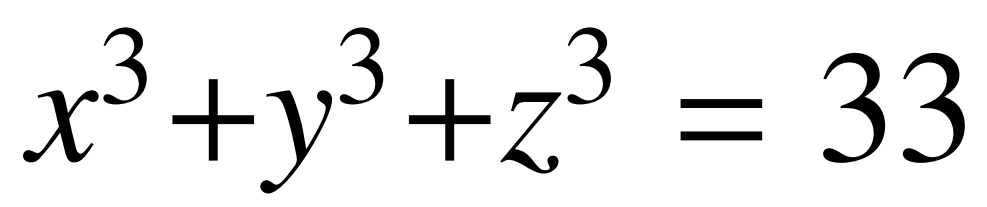這個問題，2021年，布克爾和薩瑟蘭合作發表的PNAS文章，解決了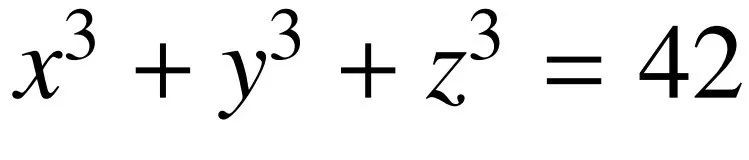這個問題，以及其他一些相關問題。

他們是怎麼做的呢？利用中學的數學知識，就可以理解布克爾的解決思路，以及33這個問題所涉及的數學和計算內容。42這個問題需要的數學要更多一些，但主要是為了提高算法的效率。這裏主要介紹布克爾的第一篇文章。

再描述一遍問題。為了便於描述，我利用了答案，把問題重新描述如下：

尋找三個正整數x>y>z>0，滿足。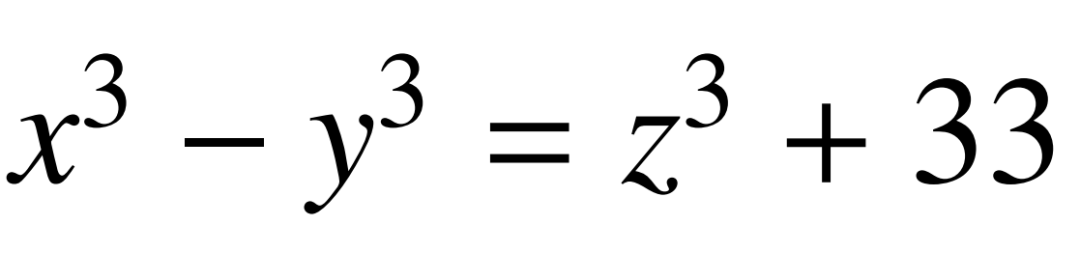

這裏不考慮(x,y,z)三個變量裏有兩個相等的情況，因為這樣涉及的計算量很少，容易驗證不存在這樣的解。

對於這個問題，蠻力搜索當然在原則上是可以的，但是太費時間，所以需要用一些數學和計算技巧。因為

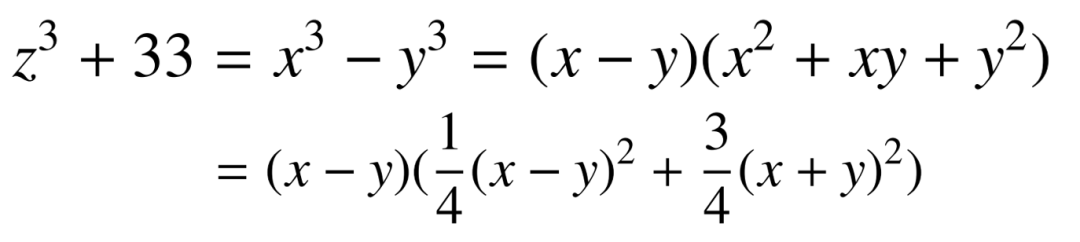
令d=x-y和s=x+y，可以得到，

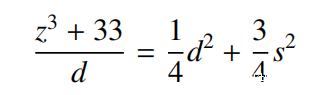
等式右邊是個整數，所以，d=x-y必須是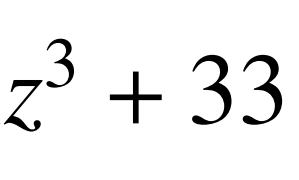的因子，經過一些簡單的代數運算，就得到

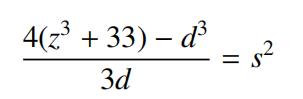
注意到等式右邊是完全平方數，所以，左邊也必須是完全平方數。

根據你的計算能力和資源，選擇一個z的上限B，比如説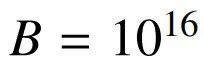，。然後，按照如下流程計算，就可以得到答案了。

1、選擇一個整數z（<B），

2、計算，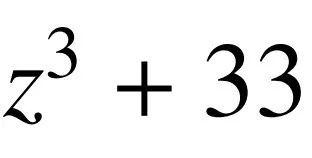

3、尋找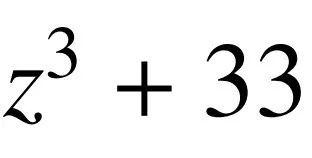的因子d，

找到一個新的因子，繼續進行步驟4；

找不到因子，或者找不到新的因子，返回步驟1，選擇一個新的整數z。

4、計算，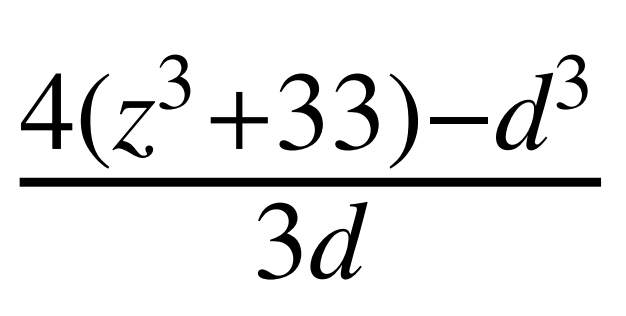

5、檢查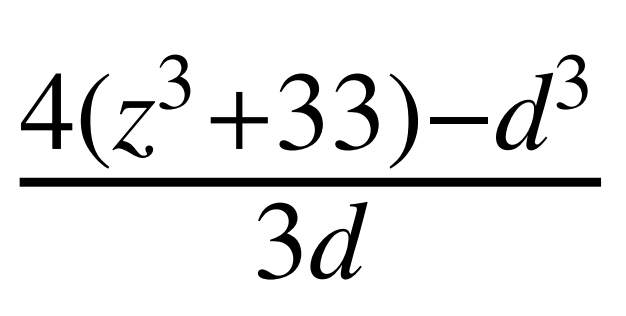是不是某個整數s的平方，

如果是平方數，就成功了，，；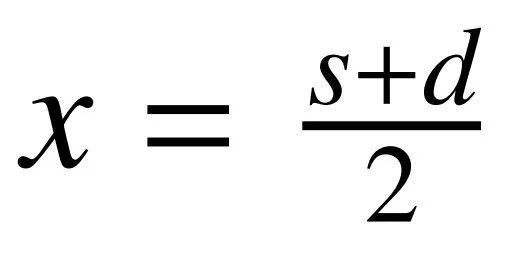

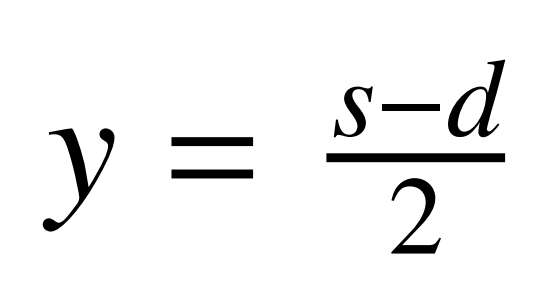如果結果不是平方數，回到步驟3，尋找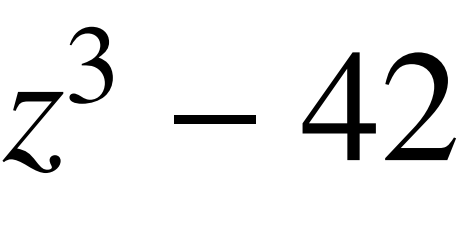的下一個因子。

上述流程的思路很清楚，但是需要的計算量仍然很大，為了減少計算量，布克爾還採用了很多技巧。有些很簡單，比如説，(x,y,z)不能是3的倍數，d=x-y有上限，等等；有一些需要初等數論的知識，布克爾教授的文章裏給出了一些引理，很有幫助；還有一些技巧相當高級，需要利用一些關於莫德爾曲線（Mordell curve）的結論，可以排除所有d≤40的情況（這部分有些困難，就不介紹了）。

利用這些限制，可以顯著減少計算量，但是仍然不太夠，主要是因為確定一個數是不是平方數，常規檢驗（也就是計算一個數的平方根）需要的計算量太大。布克爾採用了一種更有效的方案：用幾率的方法判斷一個數是不是完全平方數。他設定了一系列檢驗條件，通不過這些檢驗條件的，一定不是平方數，通過檢驗的數很少，對它們進行常規的檢驗。

這裏涉及了“二次剩餘定理”。這是初等數論的內容，概念和證明都不難，這裏只講一個非常簡化的結論。

  //  

“二次剩餘定理”有一個推論：兩個整數X和Y的乘積的勒讓德符號(XY|p)，等於它們各自的勒讓德符號(X|p)和(Y|p)的乘積，(XY|p)=(X|p)(Y|p)。

對於整數a和p，勒讓德符號(a|p)描述二次剩餘的性質，其定義如下

(a|p)=0，如果

(a|p)=+1，如果，而且存在某個整數x，使得

(a|p)=-1，如果，而且不存在任何整數x，使得

如果(a|p)=+1，就稱a為二次剩餘(mod p)；如果(a|p)=-1，就稱a為非二次剩餘(mod p)。

應用這個結論，可以快速地判斷某個數XY是不是平方數，因為計算(X|p)和(Y|p)比直接計算(XY|p)更容易。稍微具體的説，是這樣的：

1、判斷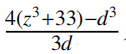是不是平方數，等價於判斷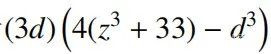是不是平方數，這個轉換隻是把除法變成了乘法，判斷起來更容易了。

2、選擇某個整數（例如）M=5×7×11×13=5005，它是四個最小素數（除了2和3以外）的乘積，不考慮素數2和3是因為前面提到的限制條件已經有效地計算了相關的情況。

3、計算3d和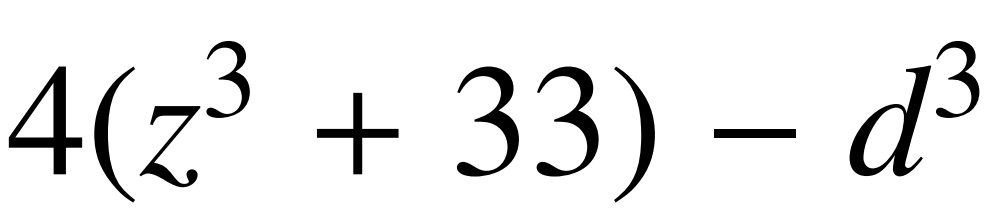這兩個數對整數M取模的餘數X和Y，計算勒讓德符號(XY|p)=(X|p)(Y|p)，這個結果只可能是0或±1。大約有一半的機會，結果是-1，這樣的數肯定不是平方數。對素數p=5,7,11,13進行這種操作，就可以淘汰掉大約百分之九十的選手。

4、對於剩下來的幸運兒，還可以用更多的素數考驗它們（需要相應地改變M），每次考驗可以淘汰大約一半的選手。

5、經過步驟3和4的篩選，就可以大大減少真正需要計算平方根的情況了。

上面是數學，下面再簡單討論一下計算。

布克爾證明了，應用上述所有技巧以後，尋找42所需的時間正比於搜索量，或者説B的大小，而相比之下，蠻力計算的用時跟成正比。事後來看，因為B是10的16 次方的量級，即使用上現在所有的計算機，蠻力計算需要的時間也很容易就超過了宇宙的年齡。

查表可以加快計算。有些數值需要經常算，把它們的結果存下來，需要的時候直接查表，這也是常用的方法，能夠“以空間換時間”——因為需要把許多表格存下來。

並行處理也可以讓計算加速。每個符合條件的z值可以單獨處理，彼此並不影響，這樣就可以把任務分配給不同的計算機（或者同一個“並行計算機”的不同的核），結果就是“人多力量大”——大家不會互相干擾，無論誰找到結果，都是最終的勝利。

編程當然也很重要。布克爾的文章裏也有描述，但是我不太懂，所以就不多談了。

利用上面描述的方法和技巧，如果z跑完了上限以內的所有值，仍然得不到想要的結果，你要麼放棄，要麼設定一個更大的上限，重複上述流程。實際上，布克爾在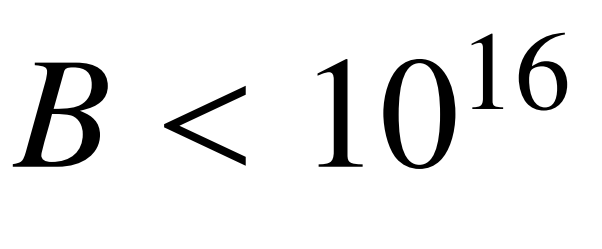這個範圍裏，只找到了33的結果，

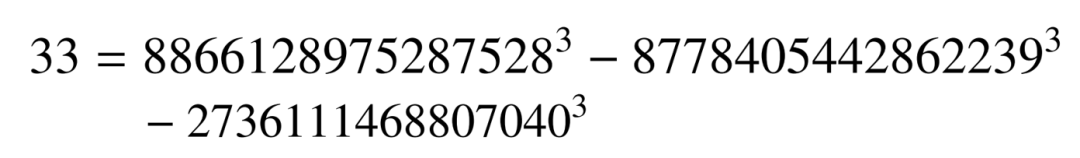
後來，他跟薩瑟蘭合作，採用了更精細的算法，在更大的範圍搜索，在全球40萬台計算機的幫助下，才得到

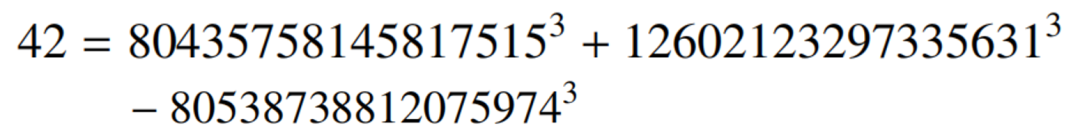
這些答案檢查起來很簡單，用筆記本電腦裏自帶的科學計算器就可以驗證，但是，尋找答案所需要的計算量卻是非常驚人的。

總之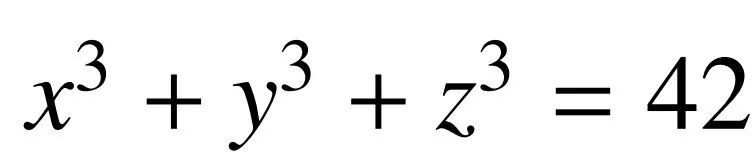，這個不定方程有整數解嗎？答案是肯定的。

難道這就是宇宙的終極問題嗎？是還是不是，這是一個問題。

後記

布克爾（Andrew R. Booker）和薩瑟蘭（Andrew V. Sutherland），還有那個證明了費馬大定理的懷爾斯（Andrew Wiles），他們的名字都是安德魯。這個名字有什麼奧秘嗎？我們注意到，安德魯這個名字有33個筆畫，也許這就是他們成功的奧秘吧。

這裏我強行規定了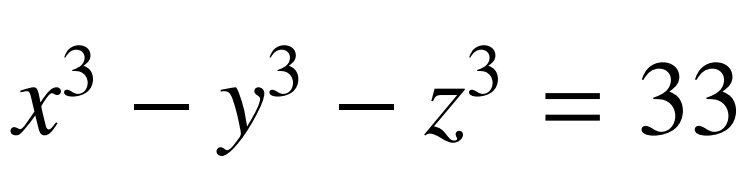這個不定方程整數解為正，並根據答案確定了它們前面的加減號。這樣描述起來很方便，但是不嚴謹——布克爾的文章是非常嚴謹的。

這裏提到的兩篇文章是：

[1]Andrew R. Booker, Cracking the problem with 33, arXiv:1903.04284. 正式發表於Res. Number Theory 5, 26 (2019)

[2]Andrew R. Booker and Andrew V. Sutherland, On a question of Mordell, PNAS 118 (11), e2022377118.

我覺得，第一篇文章很容易讀，第二篇文章要困難得多，可能是因為必須進一步提高算法效率的原因。這裏只講了第一篇文章。