李永樂翻車了？_風聞

首發於公眾號“賊叉”

那天刷微博，看見很多人at我李永樂的一條微博：

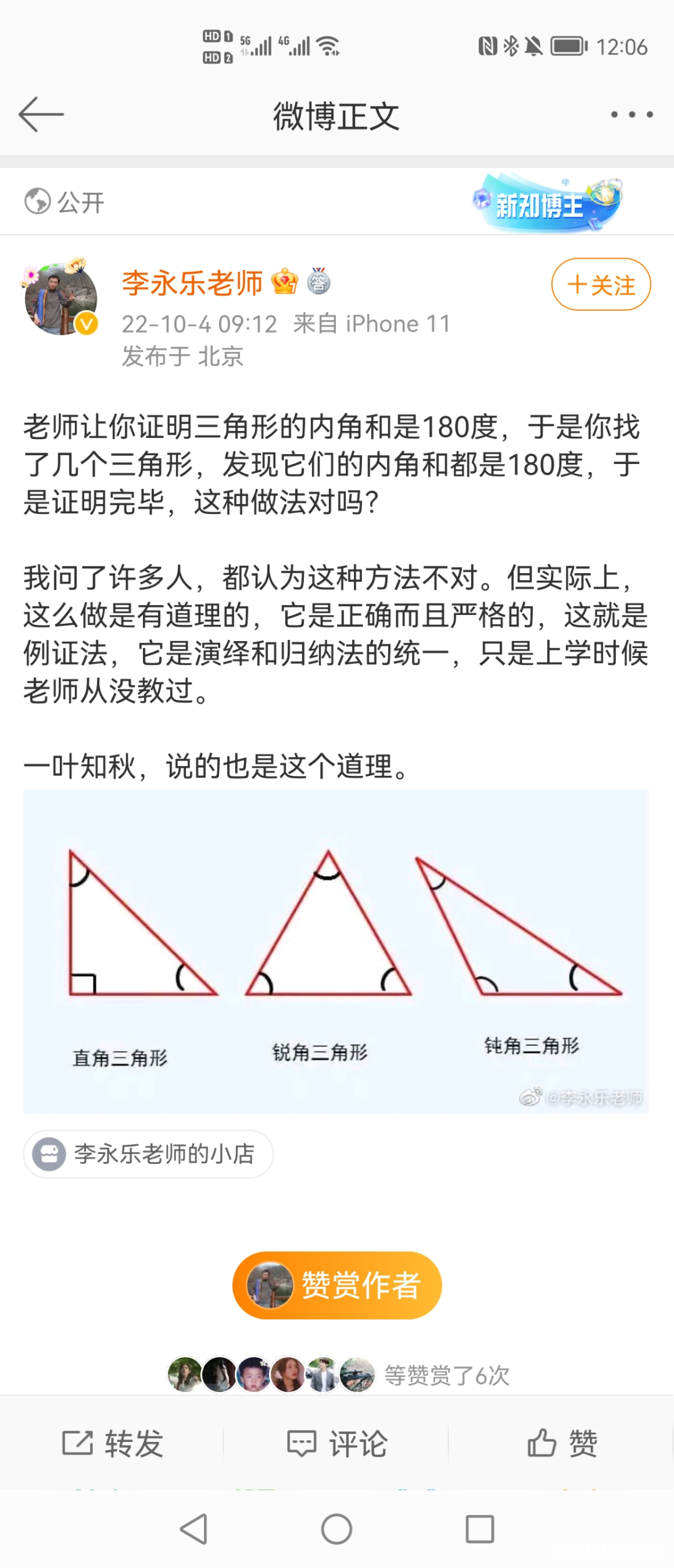
看完後我下巴都驚掉了，李永樂怎麼會犯這種錯誤？他又不是民科！

事實上，如果我們把三角形分成鈍角三角形、直角三角形和鋭角三角形，然後分別證明其內角和為180°這是沒問題的。但是你不能隨便挑幾個鈍角三角形、直角三角形和鋭角三角形，因為其內角和為180°所以得出所有鈍角三角形、直角三角形和鋭角三角形的內角和為180°的結論。

如果這可以算證明，黎曼猜想、哥德巴赫猜想和費馬大定理哪還用那麼費事？黎曼猜想的證明：因為我找到的所有非平凡零點的實部都是1/2，黎曼猜想得證；哥德巴赫猜想的證明：因為我驗證了幾個大於2的偶數，都能拆成兩個質數的和，哥德巴赫猜想得證；費馬猜想當n=3,4，5,7的時候都對，所以命題成立。

以李永樂的水平，不至於犯下這樣的錯誤吧？果然，有羣友的提示，説李永樂還有個視頻講得比較完整。於是搜了一下，找到了這樣一張截圖：

圖中，李永樂採用的是解析幾何的辦法。他先假設出三角形三個頂點的座標，然後找AC，BC邊的中點，利用延長中線一倍的方法構造出兩對全等三角形，然後證明E、C、D三點共線即可。而要證明這三點共線，只要證明直線CE和直線CD的斜率相等即可。

這種證明方法當然是沒有問題的。事實上，這裏需要用到一個結論：若經過一點有兩條直線斜率相同，則它們重合。

然而這個證明和微博中的證明完全是兩回事啊？事實上，數學中也從來沒有微博中的這種例證。一般而言，舉例是為了輔助説明猜想的正確性或者錯誤。比如當年丘成桐先生覺得卡拉比猜想是錯的，他花了四年多的時間一直在找反例，結果找了很多都是錯的。然後他就覺得卡拉比猜想是對的，又花了兩年多的時間證明了這個猜想，並因為這項工作獲得了菲爾茲獎。

同樣的，人們在探索黎曼猜想的過程中發現，別説找反例了，就連正面的例子都很難找到。後來得虧西格爾從黎曼的手稿中發現了黎曼的計算方法，從而使得計算進度大大加快，西格爾也因此獲得了菲爾茲獎。

和解決卡拉比猜想不同的是，黎曼猜想至今沒有找到反例，所以絕大多數數學家都認為這是對的。據説目前已經計算出了十萬億個黎曼-澤塔函數的非平凡零點，全都和黎曼猜想吻合，但是這也不能説明人們就證明了黎曼猜想啊？

當然，如果有反例的話，那麼只要一個就能推翻結論。比如費馬質數猜想，人們驗證了n=1,2，3,4的時候費馬都是對的，但是當n=5的時候錯了，所以費馬質數猜想不成立。然而手欠的人就有那麼多，後來人們又算了n=6,7,8……，發現這些都是合數，所以又菜只有前四個是質數，其他都是合數，到現在還沒證明呢。。。

所以無論從哪個角度來看，李永樂的這條微博中的錯誤是明顯的，千萬不能隨手舉幾個例子就當做數學的證明啊！