索菲斯·李:視力欠佳,卻看到數學和物理中最深刻的結構之一_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-10-21 10:53

撰文 | 伊恩·斯圖爾特(Ian Stewart)
翻譯丨李思塵、張秉宇
看待幾何的新方式
馬裏烏斯·索菲斯·李(Marius Sophus Lie)走上科學之路完全是因為視力太差而無法擔任任何軍職。當索菲斯——人們後來這樣稱呼他——1865 年從克里斯蒂安尼亞大學(編者注:今奧斯陸大學)畢業的時候,他只上過很少的幾門數學課,其中包括一門由挪威人盧德維格·西洛(Ludwig Sylow)講授的伽羅瓦理論,但他在這一領域並沒有表現出任何過人的天賦。他曾一度猶豫不決——他知道自己想要走學術研究的道路,但不確定應該研究哪個領域,是植物學、動物學抑或是天文學。

不過大學圖書館的借書記錄顯示,他借閲了越來越多的數學書籍。1867年的一個午夜,他茅塞頓開,看清了自己將畢生為之奮鬥的事業。他的朋友恩斯特·莫茨費爾特(Ernst Motzfeldt)在睡夢中被激動萬分的李驚醒,只見他大喊着:“我找到它了,它是那麼簡單!”
他所找到的是一種看待幾何的新方式。
李開始研究偉大幾何學家的工作,比如德國數學家尤利烏斯·普呂克(Julius Plücker)和法國數學家讓–維克托·彭賽列(Jean-VictorPoncelet)等。從普呂克那裏,他學習到幾何體的基本元素不是人們熟悉的、歐幾里得提出的點,而是直線、平面、圓這些其他的對象。
1869年,他自費發表了一篇論文,概括了他的主要思想。他認識到自己的思想正如先前的伽羅瓦和阿貝爾一樣,對於保守派來説太過超前激進,普通的期刊都不願意發表他的研究。但恩斯特鼓勵他堅持做自己的幾何研究,在他的支持下,李一直沒有氣餒。最終,李的一篇論文在一家知名期刊發表,反響熱烈。這讓李獲得了一筆資助,他終於有錢去各地拜訪頂尖的數學家,與他們討論自己的想法。他去了孕育了普魯士和德意志無數數學家的搖籃——哥廷根和柏林,與代數學家利奧波德·克羅內克(Leopold Kronecker)和恩斯特·庫默爾(Ernst Kummer),以及分析學家卡爾·魏爾施特拉斯(Karl Weierstrass)進行討論。庫默爾的數學研究方法給他留下了深刻印象,而魏爾施特拉斯的方法則沒有引起他太多的注意。
最重要的會面則是在柏林拜訪費利克斯·克萊因(Felix Klein)——他恰巧是李十分仰慕並希望效仿的普呂克的學生。李和克萊因的數學背景非常相似,但他們的風格卻大相徑庭。克萊因基本上是一個傾向於幾何的代數學家,喜歡鑽研一些充滿內在美的具體問題;而李則是一個分析學家,喜愛一般理論的全面與廣闊。諷刺的是,正是李的一般理論為數學提供了一些最重要的特殊結構,時至今日它們依然格外優美、格外深刻,其中大部分都是代數結構。如果不是李將理論推向普適化,這些結構可能根本就不會被發現。如果你嘗試去理解某個類別中所有的數學對象,並且成功了的話,你會不可避免地發現其中有很多都具備特殊的性質。
1870年,李和克萊因在巴黎再次相會。在那裏,李受到若爾當(Camille Jordan)的影響,把研究目標轉向了羣論。越來越多的數學家認識到,幾何和羣論是同一枚硬幣的兩面,但這種思想經歷了漫長的時間才全面成型。李和克萊因合作完成了一些研究,嘗試進一步明確羣與幾何之間的聯繫。最終,克萊因在他1872年的“埃爾朗根綱領”中明確地提出了這一思想,説明幾何和羣的本質是一樣的。
用現在的語言表述起來,這一思想聽起來太過簡單,早就應該是一目瞭然的了。對應於任一給定幾何的羣就是該幾何的對稱羣。反之,對應於一個羣的幾何就是以該羣為對稱羣的任意幾何。也就是説,幾何是由在羣的變換下保持不變的東西來定義的。
舉例來説,歐氏幾何中的對稱是平面中保持長度、角度、直線和圓不變的變換。它們所組成的就是平面中所有剛體運動的羣。反之,一切在剛體運動中保持不變的對象都自然地屬於歐氏幾何的範圍內。非歐幾何僅僅是使用了不同的變換羣而已。
那麼,為什麼要費力地把幾何轉換為羣論呢?因為這樣你就可以用兩種不同的方式來看待幾何,同時也有兩種不同的方式來看待羣。有的時候用一種方式更易於理解,有的時候則是另一種。擁有兩種視角總比只有一種要好。
探索微分方程
法國和普魯士之間的關係急劇惡化。拿破崙三世認為他可以通過對普魯士開戰來支撐起他下滑的支持率。普魯士宰相俾斯麥向法國發出了一份措辭嚴厲、語氣尖鋭的電報,普法戰爭於1870年7月19日正式爆發。克萊因,一個生活在巴黎的普魯士人,明智地選擇了返回柏林。
然而李是挪威人,並且非常享受自己在巴黎的訪問,於是他決定留下來。但當他意識到法國即將戰敗、德軍正向梅斯挺進的時候,他改變了主意。儘管他是中立國的國民,但在潛在的戰爭區停留仍然並不安全。
李決定迅速動身,向意大利進發。但他沒能走遠:法國當局在巴黎東南大約25英里(約40 千米)的楓丹白露抓住了他,而他隨身攜帶着許多文件,上面寫滿了難以理解的符號。由於這些符號看起來顯然是密文,他被當作德軍間諜逮捕入獄。法國頂尖數學家加斯東·達布(Gaston Darboux)介入後,才説服了當局相信那些符號是數學推演。李得以獲釋,隨後法軍投降,德軍封鎖了巴黎,而李再一次前往意大利——這次他成功了。他從意大利返回了挪威。途中他還順便拜訪了安全地留在柏林的克萊因。
1872 年,李獲得了博士學位。李的研究深深震動了挪威學術界,以至於克里斯蒂安尼亞大學同年專門為他設立了一個職位。他和從前的老師盧德維格·西洛一起,開始着手編輯收集到的阿貝爾的研究。1874 年他娶了安娜·比爾克,他們一共生下了三個孩子。
此時,李已把研究重點集中在了一個他認為發展時機已經足夠成熟的特定主題上。數學中有很多不同種類的方程,但其中有兩類格外重要。第一類是代數方程,已經被阿貝爾和伽羅瓦充分地研究過了。第二類是微分方程,是牛頓在他關於自然規律的研究中引入的。這種方程涉及微積分的概念,與直接描述物理量不同,它們描述的是物理量隨時間如何變化。更準確地説,它們給出的是這個量的變化率。例如,牛頓最重要的運動定律説的是,一個物體的加速度與作用在該物體上的合力成正比。加速度就是速度的變化率。定律沒有直接告訴我們這個物體的速度,而是告訴了我們速度的變化率。與之類似,牛頓提出的另一個解釋物體在冷卻時温度如何改變的方程,説的是温度的變化率與物體温度和周圍環境温度的差成正比。
物理學中很多重要的方程——關於流體流動、引力作用、行星運動、熱的傳遞、波的運動、磁性作用,以及光和聲的傳播等——都是微分方程。牛頓最先認識到,如果去留意我們想要觀察的量的變化率,而不是隻盯着這些量本身,大自然的規律往往會變得更加簡單,也更容易被發現。
李給自己提出了一個重大的問題:是否存在一種類比於伽羅瓦的代數方程理論的微分方程理論?是否存在某種方式來判定一個微分方程什麼時候可以用特定的方法求解?
問題的關鍵又一次回到了對稱性。李如今意識到,他在幾何上得到的一些結果可以重新用微分方程的語言來闡釋。一旦有了某個特定微分方程的一個解,李就可以對它施加(來自某個特定的羣的)某種變換,然後證明結果同樣是方程的一個解。從一個解可以得到很多個解, 全部由這個羣關聯起來。換言之,這個羣是由微分方程的對稱組成的。
這是個明顯的暗示,暗示有某種優美的理論亟待發現。回想一下伽羅瓦對對稱性的應用給代數方程帶來了什麼——現在想象一下,如果同樣的事情發生在重要得多的微分方程身上,會怎麼樣?
李羣與李代數:比想象更偉大
伽羅瓦研究的羣都是有限羣。也就是説,羣中包含的變換數量是一個有限的整數。舉例來説,由五次方程五個根的所有置換組成的羣一共有120個元素。不過,還有很多有意義的羣是無限羣,包括微分方程的對稱羣。
一個常見的無限羣就是圓的對稱羣,其中包含以任意角度旋轉這個圓的所有變換。因為可能的旋轉角度有無窮多個,所以圓的旋轉羣是無限羣。表示這個羣的符號是SO(2)。這裏的O 指的是“正交的”(orthogonal),意思是這些變換都是平面中的剛體運動,而S指的是“特殊的”(special)——旋轉不會把平面翻轉過來。
圓還具有無窮多條反射對稱軸。如果你沿着任意一條直徑反射這個圓,都會得到同樣的圓。在旋轉羣中加上反射變換,就得到了一個更大的羣,O(2)。
SO(2)和O(2)是無限羣,但屬於容易操控的一類。只要明確給出一個數——旋轉角度,各種不同的旋轉就都可以被確定下來了。當兩個旋轉組合起來時,你只需要把它們各自對應的角度相加即可。李把這種情形稱為“連續的”,用他的術語來説,SO(2)羣就是一個連續羣。而由於只需要用到一個數來確定角度,SO(2) 羣也就是一維的。
O(2)也一樣是一維的,因為我們所需要的只是一種區分反射和旋轉的方式,而在代數中這就是一個正負號的問題。
SO(2)羣是最簡單的李羣。李羣同時具有兩種結構:它既是一個羣,也是一個流形——一個多維空間。對SO(2)來説,流形就是圓,而聯結圓上兩點的羣運算,就是把兩個相應的旋轉角度相加。
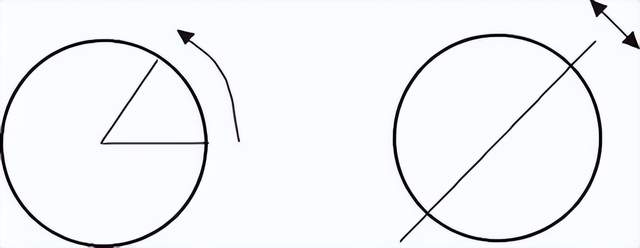
李發現了李羣的一個優美的特點:李羣的羣結構可以“線性化”。這就是説,李羣所在的彎曲流形可以被替換為一個平直的歐幾里得空間。這個空間就是流形的切空間。對於SO(2),如圖3所示。
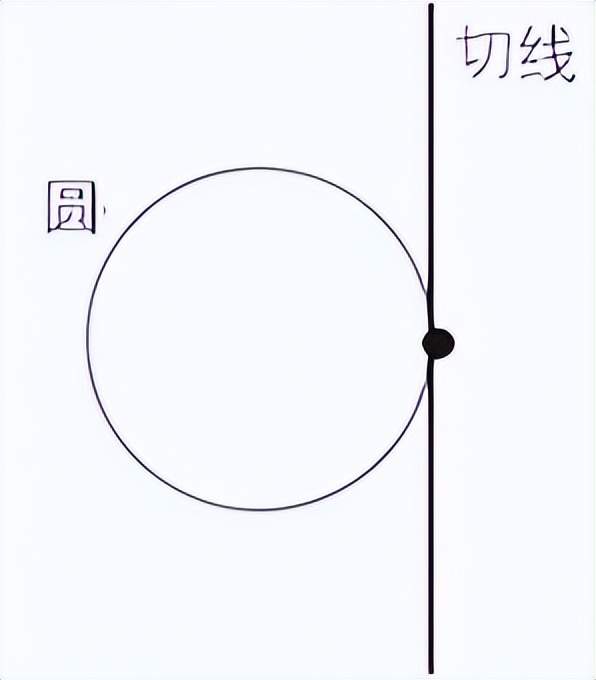
通過這種方式線性化後的羣結構賦予了切空間一個屬於自身的代數結構,這是一種“無窮小”版本的羣結構,描述了非常接近恆等變換的變換有怎樣的表現。這個結構被稱作該羣的李代數。它和羣的維數相同,但是它的幾何形式簡單得多,是平坦的。
實現這樣的簡化當然要付出代價:李代數可以捕捉到對應羣的最重要的性質,但會損失掉一些小細節,而且這些捕捉到的性質也會發生細微的變化。儘管如此,通過轉換到李代數你依然可以瞭解到一個李羣的很多性質,而且絕大多數問題用李代數都更容易解答。
可以證明——這是李的偉大洞察之一——李代數上自然的代數操作不是乘積AB,而是AB – BA 的差,被稱作換位子(在物理學中被稱作對易子)。對於像SO(2)這樣滿足AB = BA的羣,換位子等於0。但對於三維線性空間上的旋轉羣SO(3)這樣的羣,除非A和B 的旋轉軸重合或者相互垂直,否則AB – BA 不會為0。所以羣的幾何特徵在換位子的表現中得到了體現。
20 世紀初,隨着“微分域”理論的誕生,李建立微分方程版“伽羅瓦理論”的夢想終於成為現實。但事實證明,李羣理論遠比李預期的更加重要,其應用也更加廣泛。李羣和李代數的理論不再只是判斷微分方程是否可以用特定方法求解的工具,而是幾乎已經遍及所有的數學分支。“李理論”已經超越了它的創造者,變得比他能想象到的更加偉大。
事後來看,原因在於對稱性。對稱性已經深入數學的每一個領域之中,也是大部分數學物理基本思想的根基。對稱性表達了這個世界藴藏的規律,正是這些規律推動着物理學不斷向前。旋轉等連續對稱與空間、時間和物質的性質緊密相連;它們暗示着各種守恆定律的存在,比如能量守恆定律,説的是封閉系統既不能獲得能量,也不會失去能量。對稱性與守恆定律之間的這種聯繫是希爾伯特的學生埃米·諾特(Emmy Noether)發現的。
當然,下一步就是要去理解這些可能的李羣,就像伽羅瓦和他的後繼者從有限羣中整理出多種性質一樣。
此時,另一位數學家加入了這場探尋。
作者簡介
伊恩·斯圖爾特(Ian Stewart),英國沃裏克大學數學系榮退教授,英國皇家學會會員。曾獲英國皇家學會的法拉第獎章,美國科學促進會的“公眾理解科學技術獎”和英國倫敦數學學會與英國數學及應用研究院頒發的“賽曼獎章”。斯圖爾特著作頗豐,特別是在科普方面,《不可思議的數》《誰在擲骰子:不確定的數學》,Fearful Symmetry: Is God a Geometer? 等作品。
本文經授權摘自《迷人的對稱》(Why Beauty Is Truth: The History of Symmetry)(中信出版社·鸚鵡螺,2022年9月版)第10章《立志從軍的近視眼與虛弱不堪的書呆子》,有刪減,標題為編者所加。
