21世紀為什麼需要複雜科學?丨張江_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!2022-10-27 10:03
撰文 | 張江(北京師範大學系統科學學院)
2020年以來,人類社會的發展彷彿呈現出一條全新的軌跡:新冠肺炎疫情、極端天氣、俄烏衝突、股市熔斷、經濟停滯、糧食危機,這些百年罕見的天災人禍、重大事件集中、頻繁地發生。與此同時,以人工智能、區塊鏈、元宇宙等顛覆性技術為代表的高科技產業還在不遺餘力地加速推進着。人們樂觀地以為新的問題只有通過新的技術變革才能解決,但其實每一項新的發明都有可能引發新的問題和焦慮。人們不禁要問:這些意味着什麼?這個瘋狂的世界將要奔向何方?
要回答這一系列問題,應對人類百年未有之大變局,就必須站在一個全新的視角上進行系統性的思考。這一全新視角首先需要我們拋開所謂的“學科”的狹隘侷限,將古今中外各個學科的知識統合起來;其次,它既讓我們能站在全球的宏觀視角把握大的發展趨勢,又能深入細節,給出精細微妙的處理方案;另外,它還要求我們必須認識到所有這些問題都並非彼此孤立的,其背後存在着統一性。總之,我們需要一個新興的學科作為思維的腳手架,幫助我們理解這個複雜的世界。
複雜科學(Complexity Science)無疑將承擔起歷史的重任。這門從20個世紀90年代發展起來的新興學科試圖採用跨學科的方法,研究各類複雜系統背後的統一規律。儘管它還很年輕,還沒有一個普遍公認的概念體系和學科框架,但是它的跨學科範式、多尺度的研究視角以及整體論的、普遍聯繫的世界觀,足以讓它擔此重任。

早在1977年,著名化學家、統計物理學家伊利亞·普利高津(Ilya Prigogine)就憑藉“耗散結構論”這一複雜科學的開創性理論成果獲得諾貝爾化學獎。時隔近50年,複雜科學於2021年再次受到了諾貝爾獎的青睞,三名科學家分享了諾貝爾物理學獎,他們最突出的貢獻是提出了普適性的手段,並將其應用到全球氣候突變這樣的重大問題上面。

椋鳥是一種生活在歐洲的鳥,身長約22釐米,也就一個巴掌大小,但它們經常會集合形成規模龐大的鳥羣,像一隻巨大的水母飄浮在巴黎上空。椋鳥羣飛翔時井然有序,彼此不會發生碰撞;而當規模龐大的鳥羣朝埃菲爾鐵塔飛去時,又會靈活地分裂成兩個新的鳥羣,分別從鐵塔的兩側繞過,然後重新會合到一起。這種由椋鳥構成的羣體就是一個典型的複雜系統,它們不是孤立的鳥,而是通過相互協調形成了一個龐大的整體。
另一個例子是路網。很多人都有在城市中開車的經驗:每天清晨,當你開車行駛在公路上時,其實就在和路網上所有汽車所構成的複雜系統互動。每輛車都在跟隨着前一輛車,即使在沒有發生交通事故的情況下,只要車流密度很大、車速很快,一輛車的猛然剎車就有可能造成後續車輛的大堵塞——第一輛車的減速導致了後續車輛的減速,後續車輛的減速又會導致再後面的車輛減速,當這些減速連接到一起,就有可能形成由減速構成的“駐波”,像水面上的漣漪一樣順着路網傳播開來。車流、路網的相互作用也會形成一個彼此密切相關的複雜系統。

第三個例子是螞蟻。螞蟻在通過相互作用形成一個整體時展現出了非凡的智慧,如蟻羣可以通過信息素來完成彼此之間的相互作用,從而在多條巢穴和食物之間的搬運路徑中選擇最短的一條。螞蟻間的互動以及螞蟻和環境中的信息素的相互作用形成了一個複雜系統。
由此可見,所謂的複雜系統就是由大量的單元相互聯結、相互作用形成的統一的整體,這個整體表現出一定的奇妙屬性,例如鳥羣的靈活適應和整齊劃一、交通流系統中的遲滯現象形成的“駐波”以及通過螞蟻與信息素相互作用形成的最短路徑。無論是鳥羣、“駐波”還是最短路徑,它們都不能被還原為某一隻鳥、某一輛車以及某一隻螞蟻的屬性。
複雜系統中存在着很多異常複雜且有趣的宏觀現象和規律,例如螞蟻的最優覓食路徑以及黏菌的最優輸運網絡,而這些現象和規律都很難用其構成單元的特性加以解釋,我們把這類現象稱為“湧現”。複雜科學就是要研究這些不同的複雜系統豐富多彩的湧現現象背後的共同規律。用亞里士多德的一句話來概括,湧現現象即“整體大於部分之和”。它的意思是,當若干個體組合形成一個龐大的羣體時,這個羣體總會出現一些新的屬性、特徵、行為和規律,而又無法簡單地歸結到每個個體之上。
複雜系統中普遍存在着湧現現象,但是湧現並不一定限於複雜系統中。日常生活中最典型的例子是城市中的霓虹燈。我們都知道,城市中很多大樓和商店到了夜晚都會亮起霓虹燈。而所謂的霓虹燈,無非就是一堆小燈泡在閃爍,不停地變換顏色。但當你退後一步,就會看到由很多的小燈泡組成的霓虹燈整體呈現出圖案或文字,且它們無法被還原到每個單獨的燈泡上。每個燈泡的閃爍似乎都是無意義的,你只能通過它們形成的整體來解讀它的意義,這個整體的圖案或者文字就是一種湧現屬性。
進一步,集體湧現的屬性或規律可以反過來作用到微觀個體身上。例如,近年一些互聯網巨頭爭先恐後地收購和投資一些小型創新企業,從而搭建自己的“生態系統”,實際上就是在嘗試利用湧現屬性對個體的反作用這一規律。這種趨勢不僅侷限在互聯網行業,很多國家的政府和地方部門也在主動培育產業生態,希望獲得系統的力量加持。因為,隨着勢單力薄的個體聚集形成有活力的複雜系統,系統湧現出的特徵會反過來給系統中的個體都帶來好處。比如,系統內大大小小的公司會獲得更穩定的客源、更低的成本和更高的收入,相較系統外的公司有了比較優勢。

每當乘坐夜晚的航班時,我都會選擇一個靠近舷窗的位置。這樣,我就能清晰地觀察到飛機即將降落時舷窗外那座燈火通明的城市:一條條縱橫交錯的街道彷彿一條條毛細血管,公路上奔跑的汽車彷彿血管中的紅細胞,所有的毛細血管相互纏結、連向城市的中心——這裏彷彿是城市的心臟。總之,城市真的可以讓我感受到它的“呼吸”和“脈搏”,它就是一個活生生的有機體。
城市交通和人體血流是處於不同尺度、完全不同的複雜系統,前者的構成單元是車輛,後者的是細胞。上文中的類比卻讓我們清晰地看到了二者“遙遠的相似性”,比如街道網絡和血管網絡具備非常相似的複雜聯結模式,它們分別對城市的運轉和人體的代謝起到了非凡的作用。這種相似性是尋找複雜系統背後共性的出發點。
科學界有一種明星生物——黏菌,它實際上是一個由大量可以獨立自主地在環境中爬行的單細胞生物體——阿米巴蟲構成的“超級生物體”。一旦這些阿米巴蟲在多處找到了食物,它們就開始修建一條條類似“高速公路”的管道將食物聯通起來——這一切在顯微鏡下清晰可辨。更讓人驚奇的是,黏菌修建的“高速公路”竟然可以跟人類的高速公路網相媲美。2010年,日本東京大學的一個實驗小組就利用黏菌做了一個神奇的實驗。他們首先將整個東京市以及周邊36個城市的地圖等比例縮進實驗室的培養皿中,其長度大概只有20釐米。然後,他們在地圖上東京市附近的主要城市的位置上放上了阿米巴蟲愛吃的食物,再把黏菌放到東京市的位置上。一天之後,當實驗人員再次打開培養皿時,他們驚奇地發現,一張完整的高速公路網絡剛好將周圍的幾個城市和中心的東京市聯通到了一起。
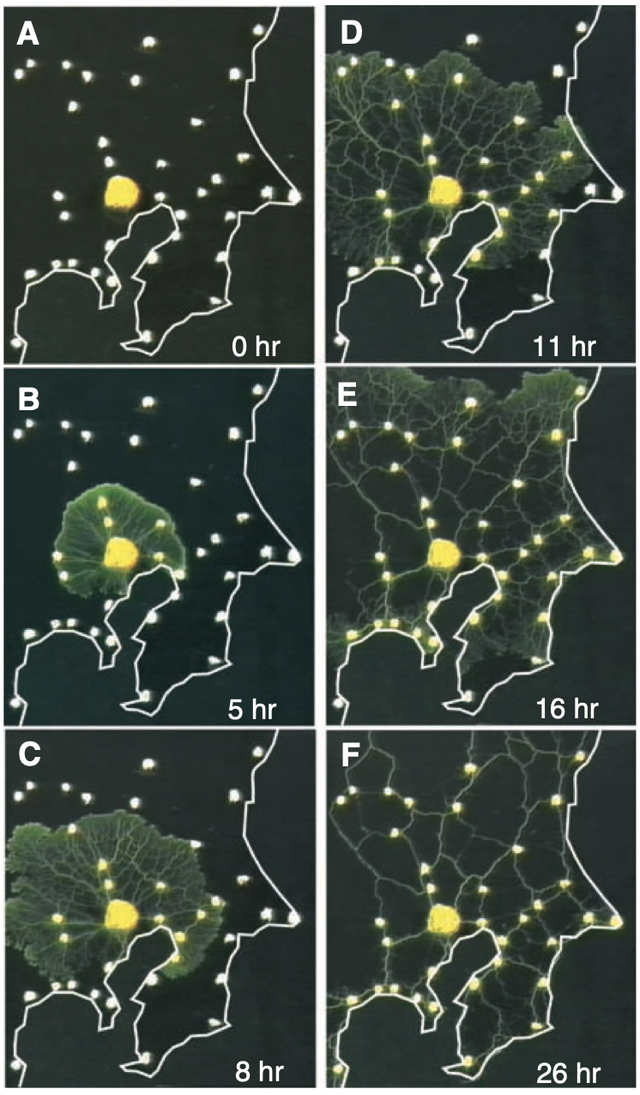
2020年,幾位研究者受到黏菌實驗的啓發,對宇宙的大尺度結構進行了研究。物理學家認為,從大尺度看,宇宙中的星系、星雲等並不是獨立飄浮的天體,而是被暗物質氣體所構成的細絲連接在一起,構成了宇宙網絡。暗物質被認為佔宇宙物質總量的85%,但難以直接探測到。於是,研究者借鑑黏菌生長的模型,設計了一種“黏菌算法”,看計算機能否像黏菌那樣“爬出”一個宇宙網絡。最終,黏菌算法計算的結果——星系間的暗物質網絡與通過最先進的宇宙學方法得出的結果並無二致。
不僅黏菌能幫我們理解宇宙,更有科學家直接拿人腦中的神經元網絡和宇宙網絡作比較。他們發現,儘管二者的尺度和形成過程差異巨大,但人腦神經元網絡結構和宇宙的一些宏觀特徵高度一致。這意味着在系統層面上,二者的演化機制可能具有類似的規律。關於人腦這個我們已知的最複雜的系統與最大的宇宙系統之間的冥冥關聯,可以加深我們對這二者本身的研究。從顯微鏡和望遠鏡裏,我們看到了複雜系統“遙遠的相似性”。

普利高津指出,一個開放的複雜系統要想朝着有序性不斷提升的方向進化,就必須讓系統保持向環境開放,以確保系統能夠從外部環境中獲取源源不斷的信息源,從而抵消系統內部的熵增。只有當系統從環境中獲得的有序(熵減)大於系統內部由於代謝作用而產生的無序(熵增)時,系統整體才有可能逐漸向有序的方向演化。無論是生物系統還是經濟社會,負熵流的持續獲取都是讓複雜系統維持生存的必要性條件。這是一條通用規律,也即著名的耗散結構論的重要推論。
耗散結構論可以説是對熱力學第二定律(熵增定律)的拓展和重新表述,並使熱力學第二定律被推廣到生物體、生態系統、公司組織、城市國家等各種複雜系統中。在中國,一個有趣的現象是,耗散結構論成為很多企業家的口頭禪,“避免耗散”“組織的熵”“對抗熵增”之類的説法非常流行。儘管多數時候這類用法不夠嚴格和定量化,例如未説明用什麼指標及怎樣度量社會系統的熵,但這一現象也體現了其理論的普適性和概念的穿透力。

著名的複雜科學家、聖塔菲研究所前任所長傑弗裏·韋斯特 (Geoffrey West)發現,諸如生命、城市、公司等很多複雜系統的新陳代謝和系統規模之間都存在着嚴格的定量關係,這被稱為廣義克萊伯定律。最早的克萊伯定律源於生物學研究。法國生物化學家馬克斯·克萊伯(Max Kleiber)早在1932年就發現,儘管不同生物體的新陳代謝率和體重不盡相同,但是它們遵循着簡單的冪律關係,即生物體的新陳代謝率與其體重的3/4次冪成正比,這意味着生物體體重增大一倍,其新陳代謝率增長近3/4倍。也就是説,新陳代謝的增長要比體重更慢,因此越大的生物體需要的代謝率其實相對來説反而更小。後續研究表明,克萊伯定律適用範圍極廣,小到單細胞內的線粒體,大到大象、鯨魚這樣的巨型動物,其適用的體重尺度範圍足足橫跨了1020之大,這在整個宇宙中都是極其罕見的。
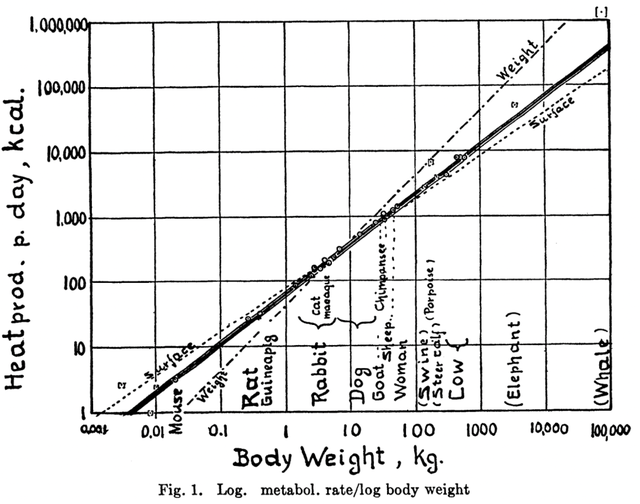
克萊伯定律意味着生物的新陳代謝率與體重之間並非簡單的線性關係,這一點往往挑戰着人們,甚至是專業科研人員的習慣性思維。曾經有一種名為LSD的致幻劑被用於動物實驗,研究人員發現貓的安全適用劑量大約是0.5毫克,於是推測體重約是貓600倍的大象的安全劑量應該是貓的安全劑量的600倍,即300毫克。在一次實驗中,研究人員將297毫克致幻劑注射給大象,但在兩個小時內,這頭大象接連經歷了尖叫、癱倒、癲癇,最終死亡。這是因理論不足而預測失敗的悲劇。事實上,動物能接受多少致幻劑或者吸收多少藥物、營養物質,都與其新陳代謝能力有關,而新陳代謝率並不是隨着體重線性增長的。根據克萊伯定律,一種體重是貓的600倍的動物,其代謝率僅僅是貓的120倍左右,也就是60毫克。因此,297毫克顯然嚴重超量了。
克萊伯定律甚至可以被推廣到企業研究中。筆者就正在和韋斯特等人合作,研究企業中的廣義克萊伯定律。如果我們將企業的總資產看作生物體的體重,將企業的淨利潤看作生物的新陳代謝率,則二者存在着類似克萊伯定律的規律,即存在着可以用冪律函數描述的定量關係,但其冪律指數與生物體的不同,這一規律在多個國家、多種市場、多個不同的歷史時期都普遍成立。
城市複雜系統同樣遵循着廣義克萊伯定律,但與生物和企業都不同的是,城市的新陳代謝與規模之間的冪律指數是一個大於1的數。直觀地説,城市人口增加一倍,城市的國內生產總值(GDP)、專利數、人均收入等都要增加超過一倍。這意味着城市越大,其新陳代謝也就越快——大城市有更多的工作機會,也擁有更高的人均GDP和財富,這解釋了為什麼人們更傾向於擠到大城市。更擁擠的環境承載了更豐富的人際互動、更頻繁的信息交換、更復雜的分工協作和更容易被激發與應用的創新想法,但新陳代謝的加快也會讓人們的生活更加繁忙,有更多處理不過來的工作郵件和更少的閒暇時光。
根據城市複雜系統的規模理論,城市大小是城市經濟發展水平的重要指標。最新研究還表明,城市規模與城市創新能力之間存在一定關係。城市要想具備創新能力,有一定的人口規模門檻。研究者甚至測算出這個門檻是120萬人,即超過120萬人的城市才可能形成創新經濟結構,並實現超線性增長。
早期城市規模研究主要針對美國的城市。美國意義上的“城市”,其範圍、聚集性、流動性都與中國不同。近年,針對中國200多座城市超過20年的數據的研究則顯示,中國城市與歐美城市的規律相似,僅在指數上略有區別,但都大於1。甚至可以基於城市經濟數據等反推真實的城市人口,修正户籍人口等統計數據的偏差。
生物體重、企業資產、城市人口對應的是不同規模大小的複雜系統。如果一個理論模型能夠穿透多個不同數量級的複雜系統,那麼它就具備了通用性和預測能力。韋斯特把相關研究總結寫進了《規模》一書,而對廣義克萊伯定律在不同尺度、領域的拓展還在持續進行中。最近有學者通過分析多種靈長類動物的大腦數據,發現大腦的白質佔比、大腦內短程連接的豐富性都隨着腦容量的大小非線性地變化。人類的腦容量最大,白質佔比達到了哺乳類動物中最高的48%。也即人類不僅有更大的大腦,人腦神經元的局部互動密度也更高,這與其腦區的高度分化和高級認知功能的出現密切相關。


同樣的,從企業的廣義克萊伯定律出發,配合上企業的財務平衡方程,我們也能推導出一個企業的生長方程,用來刻畫不同市場中代表企業在不同時期的生長行為,甚至預測其發展的天花板。
這一邏輯也適用於城市複雜系統。不同的是,由於城市的冪律指數大於1,它的生長方程會呈現出非常複雜的模式。首先,在城市發展規律的制約下,城市人口、GDP、碳排放等指標都會快速增長,在有限的時間內趨近於一個城市無法承載的最高閾值,從而將城市推到崩潰的邊緣。這就是我們看到的發生在各個國家的經濟危機或戰爭的原因。為了避免崩潰,城市必須重啓生長軌跡,唯一的辦法就是通過科技的顛覆式創新重置方程中的各個係數,將城市推入一條新的快速發展軌道。然而,城市發展在新的軌道之中仍然會遭遇同樣的問題,即在有限的時間之內,城市人口、GDP、碳排放等指標可能會再次逼近城市無法承載的極限點,新的危機需要新的科技創新,才能讓城市進入一條更新的發展軌道……
最終,在更長的時間尺度下,城市的發展曲線呈現出波動性的特點。在科技界,這是人們熟知的S型階躍式發展軌跡。每一次階躍都是一次全新的重大技術革命,從早期的互聯網革命,到大數據、人工智能革命,不同的科技革命推動了一個全新的S型發展曲線,而不同科技革命之間的間隔卻變得越來越短。用韋斯特的話説,人們不僅要不停地在跑步機上奔跑才能趕上社會發展的步伐,還要經常性地跳躍到一架更快的跑步機上。

為什麼?一切的根源都在於耗散結構和熵。我們知道,所有的複雜系統要想生存下去,就必須不斷地從外界獲取資源,以抵抗自身內部不斷的熵增,從而讓系統演化越來越有秩序。如果説人工智能、區塊鏈、元宇宙等高新技術的發展是人類城市系統的高度秩序性的產物,那麼它們的代價就是被城市複雜系統排放到外界的各種污染物和温室氣體。而且,秩序的產生和廢棄物的產生並非完全對稱平衡。事實上,由於熱力學第二定律的普遍存在,為了獲得一點點秩序,我們需要排放更多的廢棄物。城市就好比一台大空調,它不停地在城市內部製造着冷氣(更多的秩序),代價卻是不得不往外部環境中排放大量的廢熱(更多的污染物和温室氣體)。正如空調的運行會讓房間和外部環境中的整體熱量增加一樣,城市這個大空調也正在以更高的速度創造着熵,這些熵以各種不同的現象和形式表現出來。這便解釋了本文開篇提到的若干重大問題和重大事件,事實上,它們都是整個人類社會奔向奇點的必然結果。

我們不妨再次利用複雜科學的類比思維,從生物進化史上尋求解決方案。站在進化的長河之上回望,每一次重大的進化事件彷彿都伴隨着奇點的產生和複雜性在更高的系統層面以更短的發展週期進行迭代。例如,對單細胞生物體來説,多細胞生物的出現就彷彿是單細胞世界的奇點臨近。但奇點的出現並沒有讓所有的單細胞生物體死亡,而是讓它們重新集結,形成了複雜性更高的新的層級——多細胞生物。這種更高層級的個體一旦出現,進化的力量便在多細胞的層面展開,而彷彿與單細胞生物體無關了。
那麼,當技術奇點臨近,我們人類的進化是不是也會讓位於人工智能的進化,或者人類與機器的某種新層面的共生體——全球腦的進化呢?未來複雜科學的進一步發展或許可以給出答案。
參考資料
[1] TERO A, TAKAGI S, SAIGUSA T, et al. Rules for Biologically Inspired AdaptiveNetwork Design[J]. Science, 2010, 327(5964): 439-442.
[2] VAZZA F, FELETTI A. The Quantitative Comparison between the NeuronalNetwork and the Cosmic Web[J]. Frontiers in Physics, 2020, 8: 525731.
[3] BURCHETT J N, ELEK O, TEJOS N, et al. Revealing the Dark Threads of theCosmic Web[J]. The Astrophysical Journal Letters, 2020, 891(2): L35.
[4] ZHANG J, KEMPES C P, HAMILTON M J, et al. Scaling Laws and a General Theoryfor the Growth of Companies[J]. arXiv preprint arXiv: 2109. 10379, 2021.
[5] HONG I, FRANK M R, RAHWAN I, et al. The Universal Pathway to Innovative UrbanEconomies[J]. Science Advances, 2020, 6(34): eaba4934.
[6] ZÜND D, BETTENCOURT L M A. Growth and Development in Prefecture-LevelCities in China[J]. PloS one, 2019, 14(9): e0221017.
本文經授權轉載自微信公眾號“信睿週報”,原載於《信睿週報》第83期。
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。