雙曲空間漫遊指南：一場琳琅滿目的跨學科之旅_風聞

我們生活在平直的三維歐氏空間，時間空間彷彿均勻展開。但你有沒有想過，生活在雙曲空間，比如龐加萊圓盤上，會是怎樣奇妙的體驗？事實上，我們的意識、記憶或許是在雙曲空間運轉，雙曲空間是複雜網絡背後的幾何，愛因斯坦構建狹義相對論的閔可夫斯基時空也是雙曲面模型。雙曲空間到底是什麼樣？為何吸引黎曼、龐加萊、克萊因、莫比烏斯等數學巨擘探索？今天，我們共同開啓一場雙曲空間的跨學科之旅。

撰文 | 胡喬

1. 初識雙曲空間

難以想象，如果沒有畫家埃舍爾，多少人將被艱深的雙曲幾何拒之門外；幸運的是，埃舍爾的系列作品已成為最佳嚮導，指引我們通向雙曲空間。

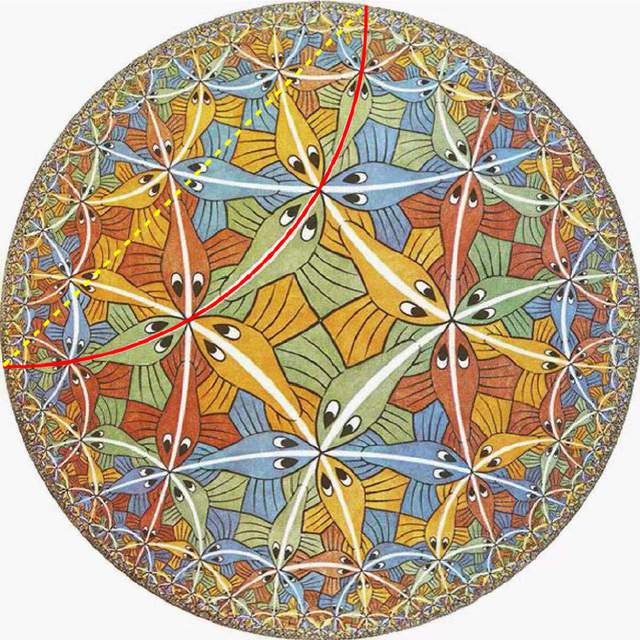
圓極限III和圓極限IV是埃舍爾創作的兩幅木刻（圖1）：前者的主要形象是各色的魚，它們有白色的背脊線和不成比例的大眼睛，緊湊排布在一個圓盤上；後者刻畫的是天使和惡魔，黑白對立，排列在同樣的圓盤上。好好欣賞這些藝術形象吧，不過我們要宣佈：圓盤才是具有魔力的，它使所有的魚都一樣大（天使和惡魔也是如此）。

圖1 埃舍爾的木刻版畫圓極限Ⅲ（左）和圓極限Ⅳ（右）

“魔力”圓盤引導我們得到以下發現：

指數增長使得圓盤極不均勻——外部緊密而內部稀疏，這也會影響長度的計算。由於每一條魚大小相等，因而可用魚長作為標尺。在圖2中，黃色虛線比紅色實線經過了更多條魚（黃線更長），這意味着兩點之間的最短距離不再是直線，而是向圓盤中心彎曲的曲線。

圖2. 圓盤上兩點的距離（紅色實線為最短路徑)

圖3. 圓盤上的三角形（圖中三角形角度趨近於0）

三條首尾相接的線段仍然構成三角形，但三角形的內角和不再是180度，而是小於180度。有多小呢，答案是可以趨於0度！

(2) 連續的層級。在圓極限IV上，每位白色天使鄰接三個黑色惡魔，惡魔也鄰接三位天使，從圓盤中心到邊緣層層展開。在圓極限III中，魚的脊線交織，也形成類似的結構。

這是不是讓你想到了無窮分叉的樹結構？樹結構有一個根節點，從根節點往外層層分叉，節點數量隨着層數指數增長。更重要的是，圓盤上的距離也近似於樹結構上的距離：在圓盤上，兩點間的最短路線偏向圓盤中心（圖2中的紅色實線）；在樹結構上，兩節點的最短距離則要經過它們共同的父節點。

圖4. 樹結構與圓盤（右圖圓盤中從A到B，可沿綠色分支，也可沿黃色點行走，距離是相近的）

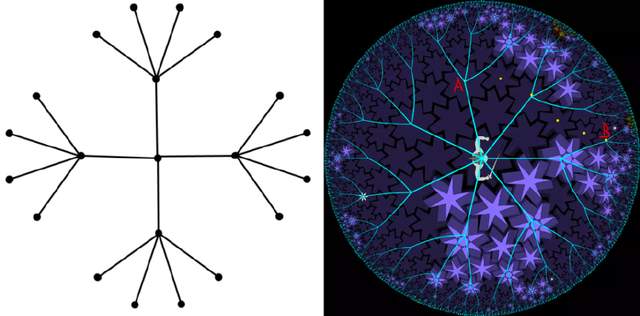
圓盤和樹的區別僅在於：樹結構的分支互不相通——如果你走錯一個分支就必須先返回到上一層，再去探尋另一條分支；而在圓盤上，你既可以按層級行走（沿着分支），也可以徑直走過去，路線更加靈活，但距離是相近的。

至此我們已經初識了圓盤模型，它是指數增長的空間，又可以看作連續的樹結構，與歐式空間大不相同——感謝埃舍爾的指引，現在可以正式介紹這個“魔力”圓盤了，它全名叫貝爾特拉米-龐加萊圓盤，也常簡稱龐加萊圓盤，是雙曲空間的一種模型。

身在雙曲空間會有何種體驗呢？舉個例子，在龐加萊圓盤上，當一個物體離開你時，它將很快縮小就像突然消失；而當它靠近你時，又會很快變大就像突然闖入——這是一個飄忽而來飄忽而去的世界。

著名的雙曲遊戲 HyperRogue 就藉助這個特性設計場景，可想而知，面對飄忽不定的雙曲世界，玩家打怪需要更加繃緊神經。

圖5. 歐式空間（上）與雙曲空間（下）的比較（動圖來源於遊戲 HyperRogue 的錄屏）

2. 細辨雙曲模型

儘管龐加萊圓盤已經廣為人知，但還遠非雙曲空間的全部。細緻地梳理雙曲空間，我們會發現有各種不同的雙曲模型，以及模型背後巨擘如雲、精彩紛呈的非歐幾何史。

曲率、鑲嵌、海珊瑚

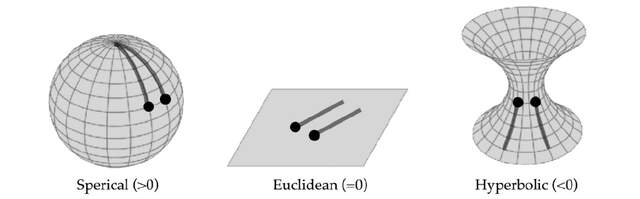
為什麼有的空間會呈現指數增長呢？這要從曲率説起。曲率衡量空間的彎曲程度，可分為三種：直線/平面不彎曲，曲率是0，圓/球的彎曲使空間封閉，還有一種彎曲使空間發散。

圖6 三種曲率

空間的大小可以用多邊形鋪貼（在數學中叫做鑲嵌）來比較。曲率如何影響空間的大小呢？來看一個例子：下圖有三種曲面，左邊的是平面，用正六邊形可以均勻鋪滿；中間的是足球形（近似球面），鋪滿這樣的球面要用一些正五邊形（黑色）來替代正六邊形，從而“節約”了一些面積；而右圖中需要填充一些正七邊形（黑色）來替代正六邊形，此時空間是翹曲的，因而增大了一些面積。

圖7 曲率與空間的大小

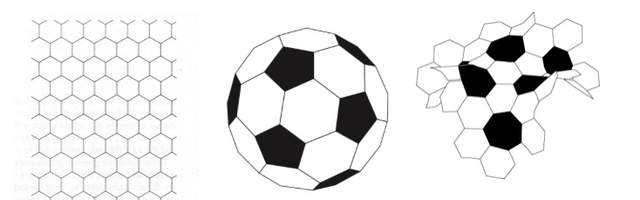
由此可知，正曲率對應的是封閉空間（如球形空間），它使空間收縮（相對於平面）；負曲率對應的是開放式無限空間（如雙曲空間）。

你可能會問，負曲率能使空間變得多大呢？首先，曲率有大小：翹曲越多，空間擴張就越多。在下圖中，每個交點處拼接了5個正方形，翹曲使得曲面多裝下了一塊正方形（相比於平面）。如果我們翹曲更多，例如在一點拼接6個正方形（實際不一定可行），空間就會變得更大。

圖8 翹曲的平面（圖片來源於網絡)

其次，空間是連續的，在一點處彎曲，鄰近的點也跟着彎曲，從單點擴展到區域，整個空間就呈現為指數增長。許多海洋生物在漫長的演化中學會了將身體舒展成雙曲空間，從而極大地擴充了體表面積：例如，海珊瑚的尺寸並不大，但如果沿着它的邊緣繞上一圈，經過的距離將千百倍的放大。

圖9 鈎針編織的海珊瑚（圖片來源於https://crochetcoralreef.org/）

圖10 銀耳（圖片來源於網絡)

至此我們瞭解了曲率這個重要概念， 而雙曲空間正是由曲率來定義：雙曲空間是具有負常數曲率的空間。非同尋常的雙曲幾何，如最短路徑是曲線，三角形內角和小於180度等，都是負曲率引起的。如果你繼續尋找還能發現更多：在雙曲空間裏不存在矩形，圓的面積和周長按同樣的速度增長，等等。

地圖投影

我們已經介紹了龐加萊圓盤和海珊瑚，你可能會疑惑，他們看起來如此不同，真的是同一類空間嗎？

這個問題可以類比地圖投影來回答：地球只有一個，但是將它展開成地圖則有很多種方式。下圖展示了常見的三種地圖投影——設想地球中心有一盞射燈，光線穿過地球落在投影面上就形成地圖。這些地圖保留了大部分球面信息，但同時也會產生變形和扭曲。例如第三張地圖（著名的墨卡託投影），在南北極附近變形就很大。

圖11 常見的地圖投影（圖片來源於網絡）

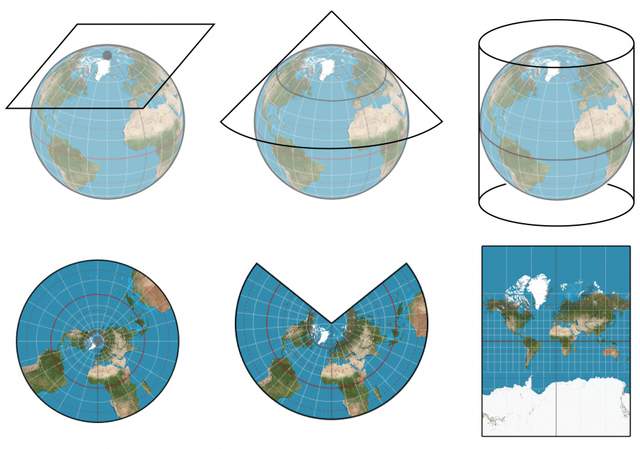
與地球-地圖投影類似，雙曲空間只有一個，而雙曲空間模型有很多種。那麼猜一猜海珊瑚和龐加萊圓盤誰是真正的雙曲空間？答案是——它倆都是投影，而真身並不可見——大數學家希爾伯特證明，雙曲空間不能等距的嵌入到3維歐式空間，也就是説我們不可能看到完整的雙曲空間。

想象整個雙曲空間是困難的， 也是令人興奮的，它一直可追溯到古希臘數學家歐幾里得的平行公設——世世代代的數學家為此追問了上千年，到19世紀終於結出了非歐幾何的碩果，使幾何學迎來高光時刻。

共形模型

最常見的一類雙曲模型叫做共形模型，共形性也被稱為保角性，是指圖形在投影前後尺寸有縮放，但形狀保持不變。龐加萊圓盤就是典型的共形模型，除了保角它還將所有空間映射到一個單位圓盤上，賦予我們上帝視角，這也是它廣受歡迎的原因之一。

共形模型的缺點是保角不保距，在埃舍爾的圓極限中，我們已經知道同一條魚投影在不同點就有不同的大小；不但不保距，共形模型計算距離的方式也比較複雜。