一個人如何被閃電擊中兩次?張益唐的新成果 | 袁嵐峯_風聞
风云之声-风云之声官方账号-2022-11-08 21:55
導言
即使看不懂這些數學細節,張益唐的奇蹟仍然可以給我們巨大的鼓舞,告訴我們人永遠都可以發揮主觀能動性,永遠都可以打破界限。最近,整個數學界最轟動的新聞是,中國數學家張益唐再次宣佈獲得重大成果,在朗道-西格爾(Landau–Siegel)問題上取得突破。呃,這話的前一句很容易理解,後一句就完全不知所云,朗道-西格爾問題是啥?

張益唐
實際上,這個新聞對我來説完全不意外。因為我2019年介紹張益唐時(質數的最小間隔有上限,人的奮鬥沒有上限 | 袁嵐峯),就提到過他在研究朗道-西格爾零點猜想(Landau-Siegel Zeros conjecture),而且對此很有信心。因此,最近的新聞完全在我的意料之中。
不過我以前並沒有調研過朗道-西格爾零點猜想具體説的是啥,現在既然他説他做出來了,我就趕快做了一番調研。然而調研的結論是,這東西完全無法向普通觀眾解釋。雖然我以前給大家講解過很多硬核的數學問題,但這次真的是太硬了。就像《是,首相》裏的經典台詞:The Russians are too strong.
然而,我可以向大家解釋清楚這事的背景。你如果瞭解這些,你的知識水平就超過了90%的人。
首先,最基本的問題是,張益唐是誰?其實張益唐現在已經非常有名了,他是數學界少有的飽經磨難、大器晚成的代表。
張益唐1955年出生於上海,1978年進入北京大學數學系讀本科,1985年到普渡大學讀博士。1991年博士畢業後,由於導師不給他寫推薦信,他無法在學術界找到工作,以至於淪落到打各種零工,才能維持得了生活這樣子。他送過外賣,賣過炸雞,還在快餐店當過會計,作過收銀員等等。有時他沒地方住,只能在車裏過夜。

打工是不可能打工的
然而奇妙的是,他在這種環境下都沒有放棄數學,仍然經常到圖書館去讀代數幾何和數論方面的期刊文章。1999年,在他的北大師弟、新罕布什爾州立大學數學系教授葛力明的幫助下,他終於在44歲時獲得了一個學術界工作:到師弟的這個系擔任臨時講師。

葛力明
2005年,張益唐50歲時,終於從臨時講師成為正式講師,因為他的微積分講得很好。按照正常的軌跡,他似乎會在這個位置上平穩地退休。
然而,命運的車輪在這時才開始轉動。2013年,張益唐在58歲時發表了石破天驚的論文《質數間的有界距離》(Bounded gaps between primes),這是人類幾百年來在孿生質數猜想(twin prime conjecture)上第一個實質性的進展。

《質數間的有界距離》摘要
什麼是孿生質數猜想?這是一個可以用小學數學知識很容易講清楚的問題,所以我們來好好解釋一下。
最前面的幾個質數是2、3、5、7、11、13、17等等,它們之間的間隔分別是1、2、2、4、2、4等等。顯然,間隔1只會出現一次,即2和3之間,因為2後面就再也不會有偶的質數了。那麼,間隔2會出現多少次呢?
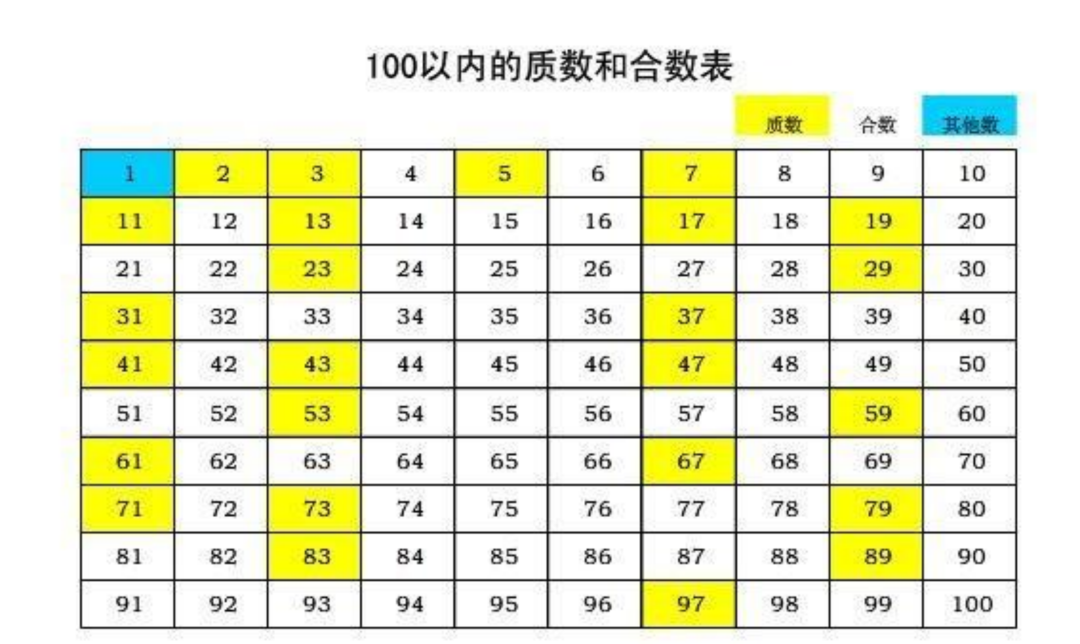
100以內的質數和合數表
一個驚人的猜想是:無窮多次!這就是孿生質數猜想。我們把一對相差2的質數稱為孿生質數(twin primes),例如3和5、5和7、11和13。孿生質數猜想説的就是,存在無窮多對孿生質數。
實際上,隨着自然數的增大,質數會變得越來越稀疏。也就是説,平均而言,相鄰兩個質數的間隔會變得越來越大。然而,孿生質數猜想説的就是,無論質數間隔變得多大,它總會在後面的某個地方突然縮小到2,這樣的事會發生無數次。
目前,我們已知的最大的孿生質數對是:2996863034895 × 2^1290000 ± 1。這是兩個大得驚人的數,寫成十進制有將近40萬位。
孿生質數猜想目前仍然是個猜想,也就是説我們還不知道它對不對,既沒有證明也沒有證偽。張益唐並沒有證明孿生質數猜想,但證明了一個它的弱化版本。張益唐證明的是:存在無窮多對質數,它們的間隔不超過7千萬。也就是説,無論質數間隔變得多大,後面總會在某個地方縮小到7千萬或以下。假如把這裏的7千萬換成2,就是孿生質數猜想。
7千萬這個數乍看起來很大,但實際上這是個重大的突破。因為在此之前人們並不知道出現無窮多次的質數間隔有沒有上限,也就是説它完全可能是無窮大,即質數間隔變得越來越大,越來越大,不再縮小。**張益唐的結果是第一次給出了一個有限的上限,即把無限變成了有限。**無限和7千萬之間是質的區別,7千萬和2之間只是量的區別。現在明白這個成果為什麼如此轟動了吧?
張益唐並沒有完全挖掘他的方法的潛力。在他的論文發表後,立刻有很多數學家來改進。他們組織了一個合作項目“PolyMath8”來做這件事,包括菲爾茲獎獲得者、著名華人數學家陶哲軒在內。
 陶哲軒
陶哲軒
通過這麼多人的努力,目前這個上限從7千萬縮小到了246。即我們已經證明了,存在無窮多對質數,它們的間隔不超過246。

PolyMath8項目的當前紀錄(http://michaelnielsen.org/polymath1/index.php?title=Bounded_gaps_between_primes)
這雖然也是不小的進步,但重要性顯然不能和最初提出7千萬相提並論。此外,這種方法的潛力似乎已經被挖掘殆盡,不足以從246縮小到2。如果想最終證明孿生質數猜想,應該會需要新的思想、新的方法。
在孿生質數猜想取得突破後,張益唐已經成為了一個傳奇。但他並沒有躺在功勞簿上,他又回到了一個他以前就經常深思的大問題,朗道-西格爾零點猜想。如前所述,我發現這個東西太複雜,無法向普通觀眾解釋。
在這裏只能稍微介紹一下背景。整個數學中有個最著名、最困難、也最重要的未解之謎叫做黎曼猜想(Riemann hypothesis),它是決定質數分佈的關鍵。我以前做過六期節目解釋黎曼猜想(黎曼猜想(六)1859年就提出的黎曼猜想,數學家證明到什麼程度了?| 科技袁人),歡迎大家去看。
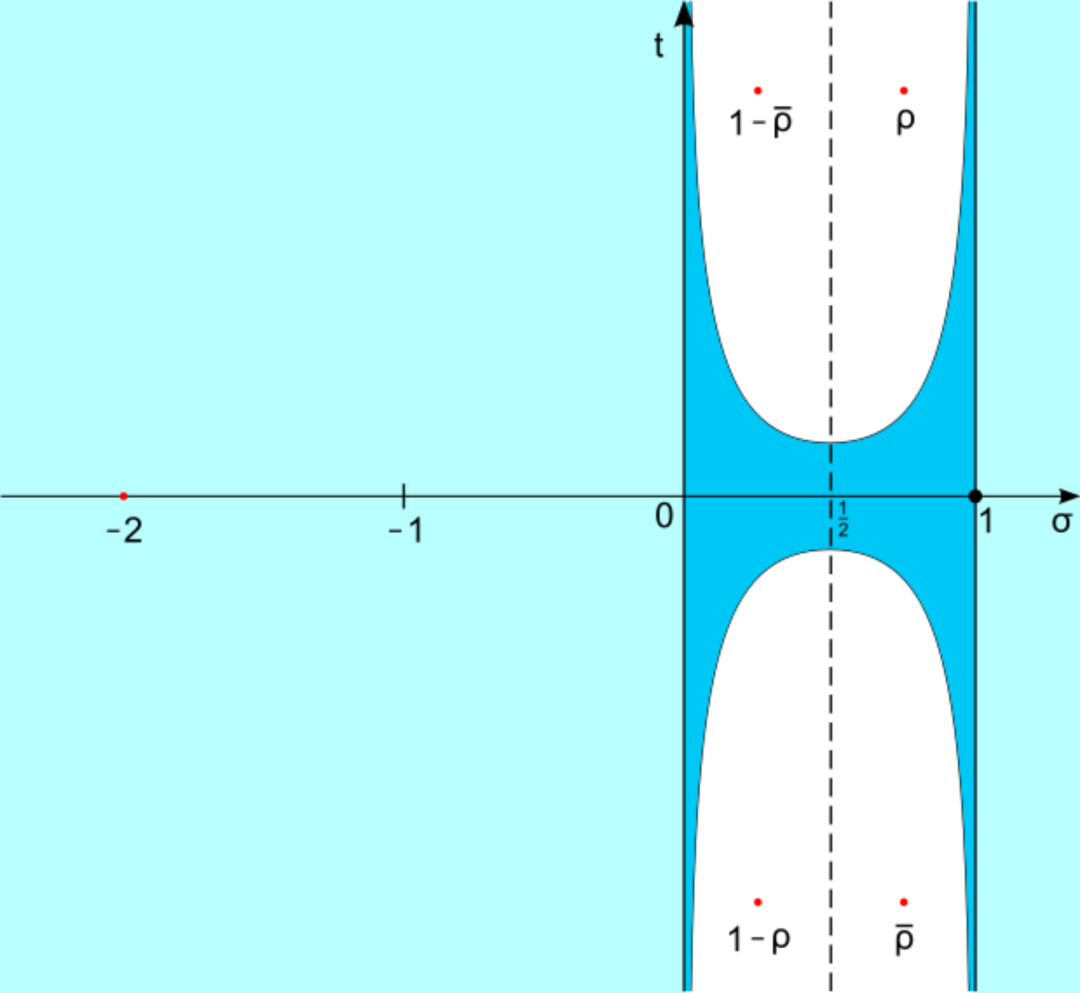
用複平面表示黎曼猜想:黎曼ζ函數的所有非平凡零點都在實部等於1/2的臨界線上
黎曼猜想已經相當複雜了,但我覺得看了這六期節目以後,普通人還能理解個八九不離十。而朗道-西格爾零點猜想是一個以黎曼猜想為背景但更復雜的問題,所以我在這裏就完全放棄了。大家只需要通過下面的敍述,瞭解這個問題的重要性就好了。

維基百科上朗道-西格爾零點的定義,如果你能看懂的話……
張益唐説:“對於數論學家來講,有兩個宇宙。在第一個宇宙裏,不存在朗道-西格爾零點。但在第二個宇宙裏,存在此零點。我們的困惑是,不知道我們到底生活在哪個宇宙裏面。”
他的同事、數論學家Stopple解釋説,如果張益唐能證明朗道-西格爾零點猜想,“就像是同一個人被閃電劈中兩次”,“如果他從未成名,那麼做出這項工作也會讓他跟上次一樣被世界矚目”。
張益唐對自己能解決朗道-西格爾零點猜想充滿信心,認為沒有大的障礙,剩下的都只是技術性問題。英國數學大師哈代(Godfrey Harold Hardy,1877 - 1947)有一句名言:“比起其他任何藝術和科學,數學更是年輕人的遊戲。”還有一句名言:“我從沒見過哪個年過半百的數學家開創重大的數學進展。”
 哈代
哈代
有人問張益唐如何看待哈代的這些觀點,他的回答是:
“這個説法可能對我並不適用。我仍然相信我的直覺,我仍然對自己有信心。我仍然有不少願景。”
目前,張益唐的論文《離散平均估計與朗道-西格爾零點》(Discrete mean estimates and the Landau-Siegel zero)剛剛發到網上,還沒有正式投稿,所以還存在出錯的可能性,要經過同行評審才有定論。如果它正確的話,張益唐就確實被閃電劈中了兩次,在58歲做出一次奇蹟後又在67歲做出另一次奇蹟。只不過對普通人來説,這後一次奇蹟比前一次難懂得多,所以我們沒法用直觀的語言來解釋。

《離散平均估計與朗道-西格爾零點》摘要
雖然無法解讀細節,我還是可以向大家解讀一下這個成果的性質:跟前一次一樣,在某個問題上取得了重大突破,但仍然沒有解決問題本身。朗道-西格爾零點猜想説的是朗道-西格爾零點不存在,由此會導出一個直接的推論,某個量大於某個量的倒數即-1次方。
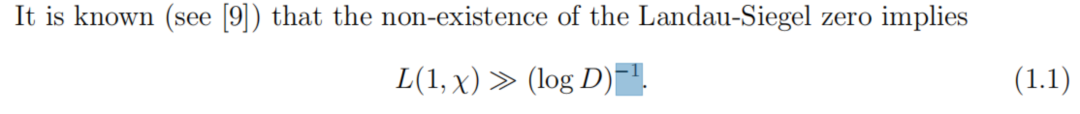 朗道-西格爾零點猜想的推論
朗道-西格爾零點猜想的推論
張益唐不能證明這一點,但可以證明一個較弱的版本,把1換成2022。沒錯,真的是2022這個數,這個亮瞎眼的數不是在開玩笑!
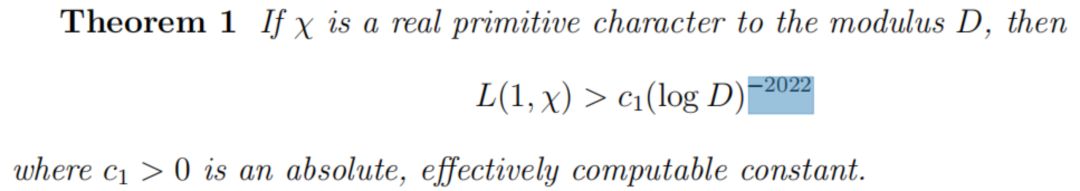
《離散平均估計與朗道-西格爾零點》定理1
張益唐在論文中也指出,2022這個估計很可能是可以改進的,就像對孿生質數猜想的7千萬可以改進。但同時,不太可能通過目前的思路把2022改進到1,就像對孿生質數猜想無法把7千萬改進到2。因此,這篇文章是對朗道-西格爾零點猜想的一個重大進展,但並不是完全解決。不過,張益唐的結果已經足以證明許多懸而未決的命題,把它們變成定理,因此這個成果確實是十分重大的。

張益唐對本文方法潛力的評估
我不久前介紹過,陳景潤對哥德巴赫猜想的貢獻也是這種性質(16個數論難題,你能看懂多少?解決多少?| 袁嵐峯)。目標是“1 + 1”,以前人們做的是“9 + 9”以至“1 + 3”等等,陳景潤做到了“1 + 2”,只差一步但還差得很遠。我想,能瞭解到這個程度,你的知識水平就超過了99%的人。

陳景潤
最後我想説,即使看不懂這些數學細節,張益唐的奇蹟仍然可以給我們巨大的鼓舞,告訴我們人永遠都可以發揮主觀能動性,永遠都可以打破界限(2019科技袁人年度盛典演講:沒有人能阻止你努力 | 袁嵐峯)。質數的最小間隔有上限,而人的奮鬥沒有上限。正如《三國演義》中,諸葛亮給周瑜的祭文中的一句話(山西大學取得量子科技重要突破,始不垂翅,終能奮翼 | 袁嵐峯):
“始不垂翅,終能奮翼!”