對付高考要不要提前學高數?_風聞
贼叉-贼叉官方账号-原浙江大学物理系博士后02-08 08:42
首發於公眾號“賊叉”
我們經常會看到這樣一些關於高考數學的言論:學點高等數學,對高考就能形成降維打擊,事半功倍!
聽聽這口氣,學點兒高等數學,説的簡直比去菜市場買二斤土豆都輕鬆。不能説相信這種觀點的都是狗腦子,只能説這腦子餵狗都不吃。
説幾個事實:**高考數學不會出超綱的題,**也就是説所有的題目一定都能用課本上的知識點所解決;
其次,高等數學是一個體系,不是説你認識高等數學這四個字,或者加上羅必塔法則和泰勒展開這九個字,你就無敵了。請注意,這是數學,還特麼是高等的,這意味着什麼你不知道麼?
從小學到高中畢業十二年的時間,除去導數的應用這一章算是和高等數學沾邊,其餘所有內容都屬於初等數學範疇。你捫心自問,學得咋樣?初等的玩意兒你都沒過關,你覺得高等數學你就能學明白了?
以同濟大學的《高等數學》教材為例,正常情況下講到羅必塔法則和泰勒展開至少要15學時以上。然而講到=會?
作為曾經主講《高等數學》的老師,我可以很負責的説,對於大多數高校來説,讓大多數學生通過《高等數學》的期末考試是高數的任課老師最為頭疼的事。千萬不要覺得自己是靠本事摸爬滾打過了高數,那是我們不知道抓掉了多少頭髮,把難度降了又降的結果。
如果你還考過研究生,體會過數一中高數的強度,就明白你高數課堂上學的那點東西根本不夠用。任何覺得高數很容易就能學會,比初等數學容易的想法都是極其幼稚的。
第三,確實存在極少數的高考數學題,如果能熟練運用高等數學的知識會很容易解決。但是那需要對高等數學知識非常熟悉,沒有相關的訓練,學生根本不會想到用高等數學去解決。甚至你告訴他這個題可以用什麼方法,他都不見得能做出來,遑論在高考時能靈活運用。
靈活運用的前提就是非常熟悉並且融會貫通,沒有大量的訓練根本不可能做到。這樣的題目在整個高考中充其量就是一個選擇或者一個填空,為了這四五分,你要搭進去多少時間和精力學習高數?這筆賬應該很容易算吧?
説了這麼多,我就舉個例子。這是某年高考真題:
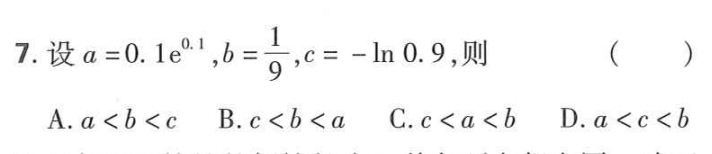
這個題用泰勒展開確實比較好做:
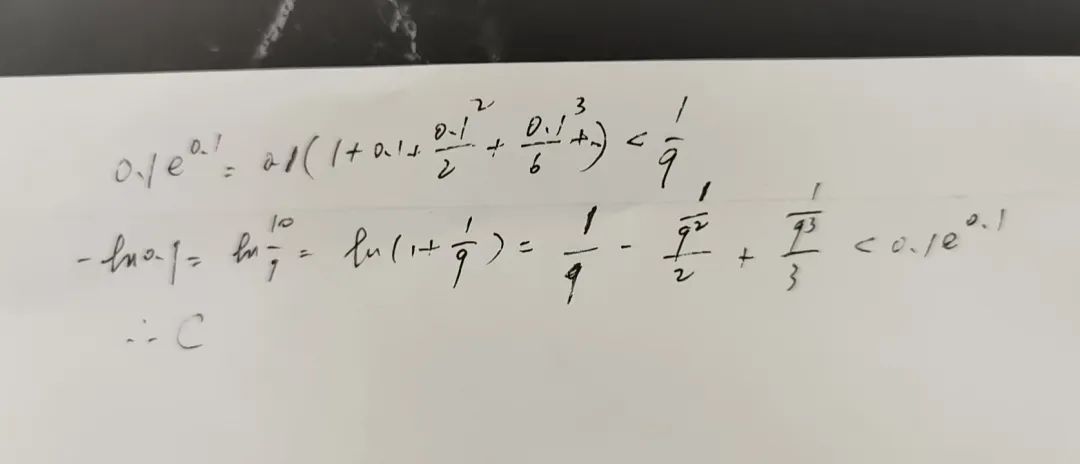
但問題我是一個教過高等數學的老師,這個內容是我們上課的時候給學生講過的。作為高中生,在高考的時候,你覺得他有多大的可能在極短的時間內馬上想到這個?
事實上,如果只用高中範圍內的導數應用,也完全可以解決,只是稍微麻煩一點:

什麼?比用泰勒級數麻煩多了?
這本來就是選擇題中的壓軸題,壓軸題誒,不要面子的啊?有點難度又有什麼奇怪的?沒有區分度的題那還叫高考題麼?
所以那些口口聲聲説讓你學高數,然後提高高考成績的,無非就是想賣課掙錢的;那些相信多學高數能提高高考成績的。。。
