《三體》最基礎的那個設定,究竟有多不可預測?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!03-15 10:05

撰文 | 邵城陽(芝加哥大學數學系博士後)
從三體到《三體》
星辰永不超越其界限(Nunquam praescriptos transibunt sidera fines)。
當龐加萊(Henri Poincaré)在論文《三體問題與動力學方程》的封面頁寫下這句格言時,他應該相當確定,自己“證明”了一個了不起的結論:
給定兩個大質量天體和一個小質量天體,假定三者之間的相互作用符合萬有引力定律,並且後者對前者的作用小到可以忽略不計。則這三個天體組成的系統是穩定的。
這正是大名鼎鼎的限制性三體問題(restricted three-body problem)。1888年,龐加萊將這篇手稿交予奧斯卡二世數學獎評選委員會,作為數學獎徵解第一題的解答:
給定一質點系,其中質點的相互作用遵從牛頓(萬有引力)定律,並假定任意二質點均不會相撞。將每一質點的座標用時間的函數表示出來,要求表達式對任意時刻均收斂。
這正是有着悠久歷史、在天體力學中佔有基本地位的多體問題。出題者是委員會成員、近代分析數學的奠基人魏爾斯特拉斯(Karl Weierstraß)。魏爾斯特拉斯相信,只要足夠精細,質點運動規律的明顯表達式是可以得到的。競賽要求參賽者匿名投稿,只在封面留下一句暗語以確認身份。龐加萊選擇了“星辰永不超越其界限”這句野心勃勃的格言。他意圖找到星辰所不會超越的界限——萬有引力作用下天體運動的規律。更確切地説,他意圖精確求解其中最為人熟知的限制性三體問題。

天文學家早已知道了太陽系內行星運動相當精確地遵從開普勒定律。翻譯成數學語言,這表示:兩個遵從萬有引力定律的質點的運動,在質心繫之下是非常規整的圓錐曲線(開普勒軌道)。但如果試圖求解某個行星的衞星——例如月球——的運動規律,那麼問題就立刻變得複雜起來,因為影響着月球運動的有太陽和地球兩個大質量天體,還不算其它離得很遠的天體造成的攝動。如果忽略月球自身的引力,而只把它當作地-日引力場中的質點,那麼我們就得到了限制性三體問題的一個相當日常生活化的例子。
這些問題從牛頓的時代開始就已經在困擾天體物理學家了。而今,龐加萊似乎精確地解出了其中一個重要的例子,完成了幾代天體物理學家的夢想;更重要的是,他引入了一系列重要的解析方法以分析天體的運動。這樣看來,奧斯卡二世數學獎授予龐加萊,可謂實至名歸;而這篇論文彷彿也將開啓完全定量描述天體運動規律的理論革命。
回顧科學史,我們知道,龐加萊的確開啓了一場理論革命,然而革命其實轉向了與最初的預期完全不同的方向。如果沒有龐加萊的工作開啓的理論革命,天體物理學家們可能要晚很久才會認識到混沌特性——某種意義上,這表示運動規律很難精確求解——才是內稟於天體力學系統的,而這一支科學理論對大眾文化的影響也會截然不同。果真如此,劉慈欣的科幻小説《三體》恐怕就需要一個完全不同的理由,讓三體文明不得不拋棄母星、開始星際殖民。“三體問題不可求解”是龐加萊成果的一種通俗説法。劉慈欣將它當作一條科學規律。他筆下的三體文明科學史,正是龐加萊故事的放大版本:野心勃勃的科學家們想要求解行星在三個太陽作用下的運動規律,然而經過一次又一次沒能預測的亂紀元災難,他們逐漸發展出相反的理論,最終證明了這個問題無法求解;生存得不到保障,於是走向星辰,走向與四光年外的太陽系勾心鬥角的未來,走向母星毀滅的未來。
需要指出的是,按照物理學界通行的表述,劉慈欣小説中的問題其實不是“三體問題”,而是“限制性四體問題”,即研究小質量質點在三個大質量質點作用下的運動,忽略小質量質點自身的影響。顯然,這裏有四個質點。這問題當然比限制性三體問題還要複雜、還要混亂。不過,説科幻作品的科學基礎“有硬傷”,並不能構成一個合理的批評。誰也不該要求虛構作品完全基於真實的設定。不論看沒看出術語問題,不論是否相信三體問題“不可求解”,都不影響欣賞作品,就好比信仰不影響欣賞其它民族的創世神話。但從科幻作品所基於的設定出發,重新審視我們所知的科學,卻仍有可能得到一些教益。就讓我們從龐加萊開啓的混沌革命開始,來看看古老又年輕的三體問題。最重要的一點,我們應該把“三體/多體問題不可求解”——還需要明確什麼叫“求解”——當作一條科學的鐵律接受下來嗎?
混沌革命
轉折開始於委員會秘書弗拉格曼(Lars Phragmén,數學家,以複變函數論工作為人所知)對結果的疑問。弗拉格曼無法讀懂龐加萊的全部論證,最終寫信向龐加萊提出質疑。龐加萊在重新檢查論文後發現了幾處嚴重的錯誤。他重寫了論文中錯誤的部分,重寫的論文刊登在米塔-列夫勒(Gösta Mittag-Leffler)主編的雜誌 Acta Mathematica 上。按照數學家伯克霍夫(George Birkhoff)的説法,這可能是 Acta 雜誌發表的在科學史上最重要的論文。它開啓了現代動力系統理論。
雖然龐加萊仍然保留了“星辰永不超越其界限”的格言,但這一次,他的論文卻給出了與預期完全相反的結論:一方面,解的滿足要求的形式級數表達式很可能不收斂;另一方面,實際上有如下的嚴格論斷:
限制性三體問題有很多相當混亂的解。
龐加萊研究的是如今稱之為哈密頓系統(Hamiltonian system)的微分方程組。這種方程組開始於一個包含2n個自變量的函數H(q, p),其中q, p都是有n個自由度的向量,分別稱為廣義座標和廣義動量。方程組的一般形式是

我們熟悉的許多經典力學系統都能夠化成這種形式,只需要取q為通常的空間座標,p為通常的動量就可以了,而這時哈密頓函數H(q, p)正是系統的總能量。它是一個守恆量。對於多體系統,除了總機械能外,總動量和總角動量也是守恆量。如果只有兩個質點,這足以導出開普勒定律。要想求解多體系統的運動規律,自然要先看看還有沒有別的守恆量。
龐加萊在論文中定義了他稱為積分不變量(integral invariant)的對象,守恆量是其中的一種。在注意到相空間體積是積分不變量之後,龐加萊證明了第一個重要結果,也就是著名的常返定理(recurrence theorem):如果相空間中的等能量面都是有界閉曲面,那麼對於相空間中每一個有界區域,不論多麼小,都有軌線可與之相交無窮多次。對於多體系統來説,這表明相流不可能特別順滑:軌線在相空間中總要時常“拐彎迴歸”。在末尾部分,龐加萊又證明了另一個重要結果:除了總機械能、動量和角動量這幾個守恆量以外,多體系統再沒有別的守恆量了!用今天的術語來説,多體系統是不可積(non-integrable)的。這粉碎了像二體問題那樣用守恆量求解的希望。
論文中段的內容包含着龐加萊最重要的兩項成果。我們先來看看跟相流的混亂特性直接相關的一項。通過選取合適的非慣性座標系,龐加萊將限制性三體問題轉化成了自由度為2的哈密頓系統。他引入了後世稱為龐加萊截面(Poincaré section)的對象:在相空間中的等能量面上,這是一個所有軌線都與之橫截相交的二維曲面,截面上的每一個點在演化中都會離開截面,而後再次與之相交。這個將曲面上的一點變為下一次相交點的映射,叫做龐加萊映射(Poincaré map,見下圖)。
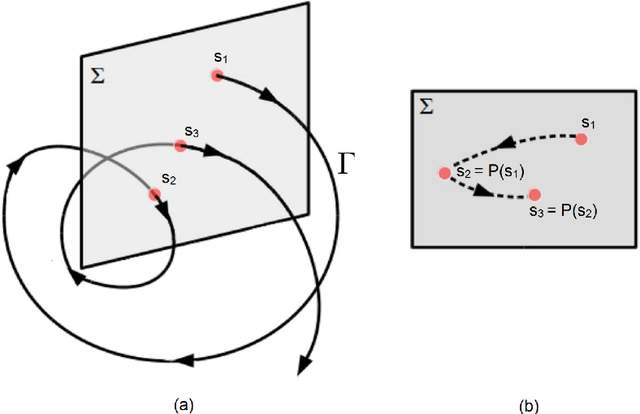
由此,研究相空間中軌線可以歸結到研究龐加萊映射P。它的不動點O對應於力學問題的週期解。龐加萊引進了現代動力系統中稱為吸引集和排斥集的對象:前者包含在P的迭代之下趨向不動點的那些點,後者包含在P的迭代之下遠離不動點的那些點。龐加萊發現,對於限制性三體問題來説,有相當一部分能量的取值,會導致相應的龐加萊映射產生奇怪的行為:它的吸引集和排斥集竟然會相交無窮多次。用今日的術語,這種交點叫做橫截同宿點(homoclinic intersection,見下圖)。如果迴歸軌線的性態,這種現象意味着:在週期解附近的軌線會無限多次地跑到離點O越來越近的地方,也會無限多次地遠離它。

後世的動力系統理論指出了這種情況下的龐加萊映射P有多麼混亂。首先,在P的迭代之下,兩個離得很近的點也會彼此遠離。從數值求解的角度,這意味着,在這些區域裏,哈密頓微分方程的解對初值的微小變化極端敏感,任何微小的誤差都有可能被放大到難以接受的程度。第二,在P的迭代之下,任何兩個點都會無限多次地越來越接近,又會無限多次地相互遠離。這意味着任意兩條解曲線都會無休止地相互糾纏、遠離。第三,在P的迭代之下,週期點構成截面上的稠密集合。這意味着微分方程又的的確確有非常多的週期解。一定程度上説,這足以粉碎“為限制性三體問題尋找好用的解析表達式”的天真願望,畢竟沒有哪種解析表達式會這麼混亂。
這些特性後來被斯梅爾(Stephen Smale)於1960年代在另一個完全不同的場景中重新發現。他的學生德瓦尼(Robert L. Devaney)將上述三條特性分別概括為初值敏感、拓撲傳遞和週期點稠密,並將滿足這三條特性的動力學現象命名為混沌(chaos)。李天巖和約克(Li and Yorke)的著名論文 Period Three Implies Chaos 則説明這種現象對於連續映射的迭代來説相當常見。自此,動力系統定性研究的時代開始了。在混沌的諸多奇異特性中,初值敏感的特性比較容易理解,它很快隨着洛倫茲(Edward Lorenz)早年發現的微分方程進入了大眾文化,並獲得了“蝴蝶效應”的雅號:“蝴蝶扇動翅膀,可能引發一場龍捲風”。然而,我們應該記得,這種現象最早是龐加萊發現的。可以説,龐加萊的工作開啓了混沌革命。
遍歷性疑難
龐加萊的工作迫使物理學家們大大修正自己的直覺。毫不誇張地説,從1920年代開始,在相當長的一段時間裏,這種直覺擺向了另一個極端:相信一般的力學系統都相當地“混亂”。彼時還沒有“混沌”這個概念,那麼“混亂”在這裏是什麼意思呢?

如果ω是有理數,那麼軌線會繞着環面轉幾圈之後回到起點,轉的圈數取決於ω的分母有多大。但如果ω是無理數,那麼情況就要複雜得多了:軌線無論如何也不可能迴歸起點,而且至少根據我們的數值實驗,它似乎要穿越環面上的每一個區域。實際上還會有更強的結論:給定環面上的區域Ω,則在Ω內部的軌線之長度佔軌線全長的比例,會漸漸接近Ω的面積佔整個環面的比例。
學過微積分的讀者不妨試着將這個結論用極限的語言表達出來,並作出證明(提示:三角級數)。在現代數學術語中,這種“均勻地遊遍全世界”的現象叫做“時間平均等於空間平均”——遍歷性(ergodicity)。這個概念最早由物理學家玻爾茲曼(Ludwig Boltzmann)在1870年代研究統計力學時提出,而將其定義嚴格數學化的,正是前文提到的高度評價龐加萊工作的伯克霍夫。玻爾茲曼提出了遍歷性假設:一般的統計力學系統都有這種“時間平均等於空間平均”的性質。

玻爾茲曼針對的是有着巨量粒子的系統,而龐加萊所證明的常返定理卻提示説,“簡單”如三體系統的哈密頓系統,也可能會“均勻地遊遍全世界”。物理學家們由此開始相信,一般的哈密頓系統也會有這種混亂的遍歷性質。費米(Enrico Fermi)正是一個嚴肅對待這一假設的物理學家。在1923年,費米發表了一篇文章,試圖證明如下結論:在龐加萊常返定理的假設之下,哈密頓系統在相空間中的等能量面上是遍歷的。儘管當時這被物理學家廣泛地接受,而且還有不少數學上的證據側面支持這個猜測(例如伯克霍夫的個別遍歷定理),但他的“證明”其實是不對的——不是物理學家所熟悉的“數學上不嚴格”,而是我們後來知道這個結論本身是錯的。
然而我們不該由此苛責古人。費米不愧是偉大的物理學家,他雖然給出了“證明”,但仍然相信物理直覺需要經過實驗檢驗。在1950年代,費米小組開啓了一項數值實驗,用著名的MANIAC I計算機(它是第一台在棋牌遊戲中擊敗人類的計算機)演算了兩個包含64個粒子的力學模型。它們如今被叫做FPUT模型(Fermi-Pasta-Ulam-Tsingou model)。費米小組原本期望能夠通過數值演算觀測到很強遍歷特性,然而結果卻令他們感到驚訝:所有的解最終都變得非常“規律”——數值結果顯示,它們最終都越來越接近上文提到的那種擬週期函數。雖然也算得上有遍歷特性,但程度卻遠遠稱不上混亂。研究小組在1955年的報告中失望地總結道:“計算結果幾乎沒有顯示出任何趨向能量等分(注:等能量面上遍歷性的推論)的可能性。”
這種境況完全可以叫做“遍歷性疑難”了:實驗結果和理論直覺完全不符。從今人的視角來看,我們可以這樣解答疑難:在常返定理和遍歷性質、乃至完全的混沌之間,還有着許許多多的可能性。龐加萊的工作,在一定程度上導致了矯枉過正,讓學者們在相當一段時間裏忽視了其它的可能性。
絕處逢生:KAM
其實,從最基本的常識出發,要找出能夠説明遍歷性疑難的例子再簡單不過了:為什麼我們能夠看見太陽和月亮日復一日地、穩穩當當地東昇西落,而不是像三體世界裏那樣混亂到不可預測?按龐加萊的研究成果,“理論上”來講,三體系統的解“有可能”相當不穩定,那麼為什麼高懸的日月恰好就沒有處在這種可能之中呢?
一個直接的解釋是:我們所處的太陽系可能具有混沌特性,但是混沌特性卻也未必意味着星球會到處亂飛,而可能只是體現在公轉相位上的混亂;另外,以人類的觀察尺度,不穩定性可能需要相當長的時間才能夠體現出來,我們很難直接察覺到。總之,它的混亂不像《三體》小説中那樣,暴烈到能輕易毀滅上千輪的文明。
這種“混亂但温柔”的解釋很好地平衡了理論與常識,而且也有越來越多的天文學證據支持這種解釋。然而,仔細想來,它其實巧妙地繞開了我們關心的核心問題:一般的哈密頓系統到底有沒有遍歷特性?
如果站在1954年就去世了的費米的角度,問題的答案恐怕相當出乎意料:有很多一般的哈密頓系統雖然不可積,但卻並沒有遍歷特性。這個回答主要歸功於三位重要的數學家:柯爾莫戈洛夫(Andrey Kolmogorov)、阿諾德(Vladimir Arnold)和莫澤(Jürgen Moser),他們的系列成果因此簡稱為KAM理論。


科爾莫戈洛夫其實沒有完整地證明這個結論。第一個給出完整證明的人是他的學生阿諾德。莫澤從兩人的工作以及納什(John Nash)的工作裏汲取靈感,將迭代方法抽象出來,成為了現代分析數學中一套強有力的方法,即所謂的 Nash-Moser 定理。KAM 理論極大地推動了分析數學裏許多分支的發展,可謂是分析數學輝煌的篇章。
總之,出乎費米(以及同時代的許多物理學家)意料的是,一般的哈密頓系統其實並沒有那麼“混亂”——被擾動的可積系統不會滿足遍歷性假設。這種系統的軌線儘管複雜,卻有很可觀的部分被限制在相空間裏的低維環面上,在很大程度上是可以預測的。這跟那種“混沌得出奇”的情景還是不一樣的。
星辰之限
那麼,既然有KAM理論作保證(雖然這屬於後見之明),為什麼龐加萊還是能夠發現混沌現象呢?這其實是因為這兩種理論的適用範圍完全沒有交集。KAM理論適用於相空間裏這樣的一些區域:擾動h的大小與h0相比很小。但在龐加萊所討論的限制性三體問題裏,第三個天體被假定具有比較大的機械能,幾乎接近能逃逸大質量天體引力的水平,這遠遠超過了KAM理論起作用的範圍。所以,KAM理論所保證的“小能量”下的穩定性,與“較大能量”之下出現的混沌特性之間並不矛盾。
這樣一來,就出現了一個很有意思的問題:KAM理論能適用的範圍到底有多大?特別地,能大到覆蓋太陽系中的天體運動嗎?
阿諾德提出了這樣一個定理:對於有一個大質量恆星和許多黃道面幾乎共面的行星的系統來説,KAM定理能夠保證它們的開普勒軌道在擾動之後仍有一定概率是擬週期的。理論上,這似乎是太陽系穩定性的有力保障。可惜,在最早的版本中,KAM型定理所要求的微擾的尺度都小得出奇,遠遠小於天體之間質量的比例。另外,更本質的問題在於,許多重要的天體運動問題的哈密頓函數遠遠不滿足科爾莫戈洛夫要求的非退化條件。
不過這些“理論上的”成果卻足以提示我們:在許多可以視作微擾問題的情境裏,KAM理論的機制儘管未必能夠保證擬週期解的穩定性,卻暗示這種穩定性是可以預期的。例如,在太陽-地球和月球組成的三體系統裏,月球公轉軌道同地球黃道面的夾角僅有5°左右,非常接近於三星共面的三體系統。雖然沒有任何已知結果能夠保證這個系統的穩定性,但KAM理論的存在卻暗示我們,有一定可能證明它的穩定性。對於整個太陽系來説也是如此:這個系統穩定或不穩定的斷言都各有證據支持,現在還遠遠沒有到最終下決斷的時候。
另外,KAM理論的某些改進版本也能夠給出一些天體力學上的推論。例如,在2003年,Celleti和Chierchia就證明了太陽-木星-凱神星的限制性三體系統適合KAM型的結論,從而擴展了KAM理論的適用範圍。從實際的角度來説,這表明:作為小行星一員的凱神星的軌道是很穩定的,儘管有木星巨大的引力所引起的攝動,它也並不會突然偏離原有軌道橫衝直撞。他們的證明是由計算機輔助完成的,因為計算微擾級數的工作決非人力可及。
實際上,人們也已經開始藉助計算機去尋找三體問題的特解了。例如,在2017年,上海交通大學廖世俊研究小組得到了等質量三體問題的695族週期解(見下圖),此後更是將數量擴展至1349族和135445族。《三體》小説中,地球三體組織中有一派將求解三體問題作為向“主”表達愛戴的儀式,在故事中,作為局外人的魏成“取得突破”,找到了上百族解,激起了地球三體組織的內訌。看起來,作者為小説所虛構的研究成果,在計算機技術的實際進展面前已經有些落後了。當然,人們可能暫時還沒辦法更深入地研究這些週期解的穩定性。不過,這些進展都提示我們,三體問題本身是非常複雜的:這裏的“複雜”不是指絕對不可近似求解、不可預測,而是指它的解可能有許多種截然不同的表現:其中有些“混沌”的解會導致不可近似計算、不可預測;有些儘管“混沌”,卻因為時間尺度太大的原因而仍然可以預測;而有些雖然複雜,卻並非不能精確地求解。龐加萊證明的是“三體系統不可積”和“三體問題在某些能量區域展現混沌特性”,由此就作出“三體問題不可求解”的結論,其實有些粗疏。

距離龐加萊寫下那句格言已經過去了一百三十多年。在這些年間,人類對於天體運動規律的認知經歷了好幾次劇烈的變化。我們有充足的理由相信,我們對這些規律的認識還遠遠不足,現有的認識框架也很可能會再次被顛覆。二十世紀裏計算機技術尚不發達的時候,數理科學家就已經想到了別的辦法去描述限制性三體問題在混沌區域的表現。儘管這些描述只是進一步揭示它在混沌區域的不可預測性,但誰知道人類將來能不能找到全新的認識框架,從而重新定義“可以預測”這件事呢?
星辰的界限是無窮無盡的,它需要兩種非凡的勇氣才能探索。面對複雜的境況,要有勇氣直呼其名。為了直呼其名,則需要不斷使用新的技術、新的語言,發展新的思維方式,而這就需要另一種勇氣:準備好與習以為常的直覺決裂。
尾註:《三體》小説中提到的三體問題本身未必處在混沌的區域裏。也就是説,這三顆恆星本身的運動未必會複雜到完全不可預測。實際上,真正不可預測的乃是那顆行星的運動。人們尚不知道,對於三顆恆星來説,限制性四體問題的混沌區域究竟在哪裏?它本身又是否有穩定的區域,或者KAM理論能夠應用的區域?這樣看來,有三個太陽的行星是否可能有宜人的環境——與人類熟悉的地球環境相接近——其實是一個非常開放的問題。對科幻小説的設定較真,未必是抬槓。



