計數單位，一個胡編亂造出來的多餘且荒謬的偽概念？兼談數位與數級兩個概念_風聞

**【請教：**想問下上世紀八九十年代上小學的朋友們，當時的數學中有”計數單位“這個麼東西嗎？】

導讀

“數”有單位嗎？沒有！“量”才有單位。

漢字數字一、十、百、千、萬、億是單位嗎？不是單位，而是表示數的數字和用該數字表示的對應的數（各個數字既可以單獨表示對應的數又可以與其它數字組合表示其它/更多的數）。

類似100萬這樣的對1000000或者説一百萬這個數的表述/書寫方式，只是實際使用/書寫過程中的一種約定俗成的便宜行事的簡略寫法而已，而並非因為數學中還真有什麼“計數單位”這樣的基本概念因而在數學上可以將1000000這樣的數寫成100萬或1000千（所謂1000k）。類似的，英語中的one、ten、hundred、thousand、million、billion、trillion難道是計數單位嗎？並非如此，它們也是表示數的數字或者説為了讀其它符號（阿拉伯數字記數系統傳入歐洲後歐洲就採用阿拉伯數字記數系統了）書寫的數而發明的讀法（對應的是數的讀法中的數級），而10 billion這樣的表述/書寫方式，billion也並非單位，而只是一種因利乘便的簡略書寫方式而已。

我不知“計數單位”這個名詞是數學中原本就有的基本概念，還是在實際教學中不知從何時起方才編造出來的一個“説法”。我只知道——經過了一番研究後才知道——“計數單位”直到2022年版新課標才被增加進入課標，也就是説，即使早前已經將“計數單位”作為基本概念編入教材，但課標中卻沒有。

此一事實，不是足堪玩味嗎？

---

引言

直到在孩子的作業中發現有關於計數單位的習題，我才第一次知道還有“計數單位”這麼個概念，敢情我當年上的是假小學？

習題

3703408的最高位是    百萬位   ，最高位上的計數單位是   百萬  。

以下是所謂的相關知識點：

計數單位：一（個）、十、百、千、萬、十萬、百萬、千萬、億。

數位：計數單位所佔的位置。例：個位、十位、百位、千位，萬位、十萬位…… 

口決：有“位”是數位，沒“位”是單位。

我的第一感覺是這可能又是教學過程中為了所謂的便於理解而引入/發明——其實是生造甚至是胡編亂造——的中介性的“説法”。但轉念深入一想，似乎也不對啊，都出現了這樣的習題，説明它已經不是一個輔助性的中介性的説法了，而是一個正經的數學基本概念了。查閲了教材發現，“計數單位”真的就進入教材了，而且是作為基本概念來表述的。

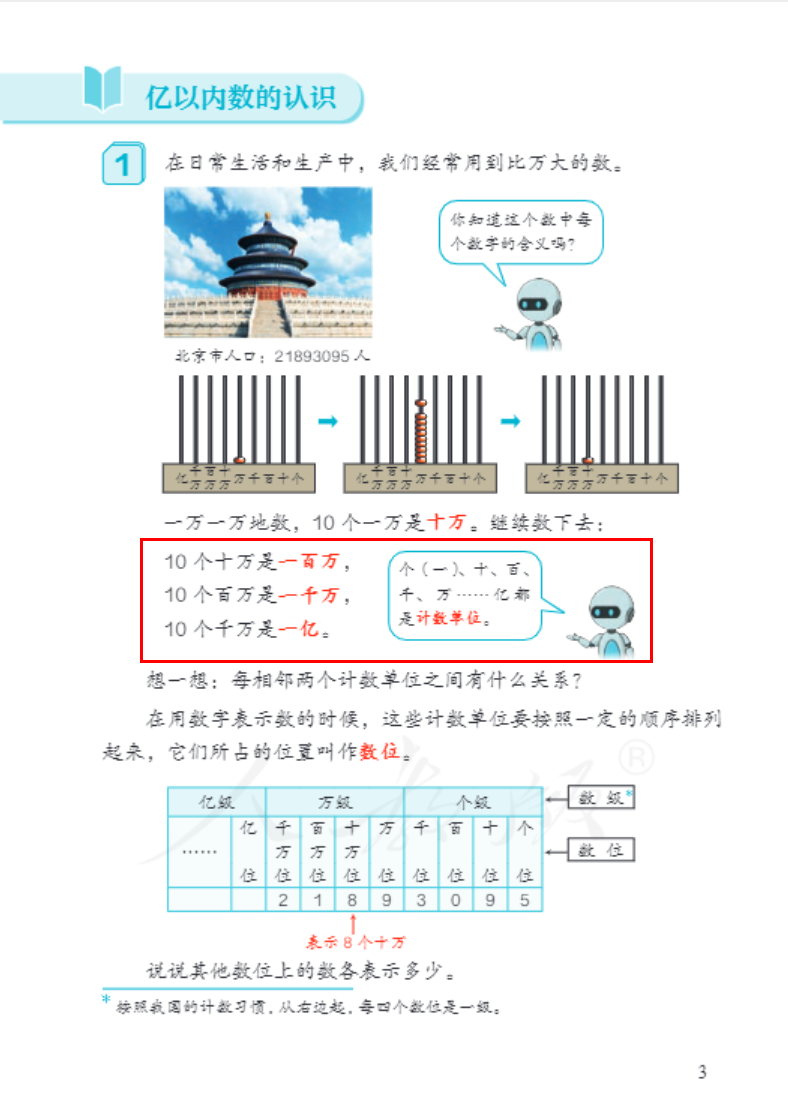
人教版教材（四上）

於是，我有點惴惴不安，同時也慚愧於自己的見識淺陋。

但是，我還是感覺“計數單位”這個所謂的“概念”不對勁，與我的直覺格格不入。

想起眉山劍客陳平老師的教導，“當你發現你的直覺和既有理論/認知相矛盾時，相信你的直覺，大不了實在錯了再改，這樣才能做出突破和創新。”

是故，我對此做了點小研究，研究結果一定程度上印證了我的直覺認知。

一、計數單位與數位究竟有何區別

教材中的表述：

一（個）、十、百、千、萬……億都是計數單位。

在用數字表示數的時候，這些計數單位要按照一定的順序排列起來，它們所佔的位置叫做數位。

做一做：

讀出下面各數，然後把它們改寫成用“萬”做單位的數。

那麼所謂的計數單位與數位的區別就文字表述表面看，無非兩點：

1、計數單位如十、百、千、萬、億後面不加一個“位”字；

2、打頭的“一（個）”與“個（位）”之別。

那麼問題來了：

1、書面上的嚴格區分——體現於還要將此作為知識點來出習題甚至考題——與實際讀數習慣上有衝突。

我們都知道或者説習慣於，讀一個數的時候，我們先要按從右至左的順序去識別最高數位（挨次點遍各個數位，或者在學了數級後便捷識別），在識別/點讀的時候，沒有哪個傻瓜會帶着一個“位”字——如個位、十位、百位、千位、萬位、十萬位、百萬位、千萬位、億位——去點識的，而只會不帶“位”這個字去點識如個、十、百、千、萬、十萬、百萬、千萬、億，但我們都清楚地知道我們點識的就是數位，同時也是我們將這個數讀出來時將要用到的計數單位——姑且用一下計數單位這個説法。

稍微做一點概念區分也未嘗不可，學生會讀數了就行。非要將其作為一個知識點來考察，就有點過分了，反而讓孩子們覺得無所適從，給弄暈了。

2、打頭的計數單位的“一（個）”與數位的“個位”各自的“個”如何區別。

計數單位的“一（個）”這個表述究竟啥意思，“一”的後面跟着個“（個）”究竟是要表達啥意思？計數單位的這個“（個）”與數位的“個位”中的“個”有區別嗎？如果有區別，又各自表達啥意思呢？

教材沒有解釋，我查閲了好多資料包括很多網上的好多老師發的教案，都對此諱莫如深。

我猜，計數單位的“一（個）”裏的“個”是為了註釋前面的“一”的，意思是“個位”上的不滿“十”（注意，我這裏沒用“10”）的數（這裏用“數”還是“數字”呢，又是個問題）。但是對計數單位的解釋竟然用到了“數位”的概念，又有不妥，因為按教材的表述，計數單位的概念在先而數位的概念在後——教材表述“計數單位按一定順序排列起來，其所佔位置叫數位”。

那如果計數單位的“一（個）”中的“個”與“數位”中的“個（位）”沒啥關係，那就只能算是一個普通的表示具體事物的量的量詞咯。然而，這就更不靠譜了，一個表示抽象概念“數”的基本概念居然跟一個具體事物的量詞給拉郎配到一起了，太彆扭了，也太荒唐了。

如此看來，確實是不可説、不能説，因為説不清嘛。

那麼，在老師也講不明白（本質）的情況下，孩子們遇到關於計數單位和數位的題目，其結果必然是，被整懵了，嚴重一點的，就會覺得數學不友好，動不動就“設計陷害ta”。

當然，背背口訣，吃過幾次虧，題目或許都能做對，但是孩子們學到了啥呢？一個雞肋般的甚至是有害無益的“知識點”。

課標中的解釋/表述也大有問題。

課標修訂小組組長的PPT截圖

先看這句：“數是對數量的抽象。”

數量是啥？用數結合物理的量的計量單位來表示的物理的量的多少。數量這個概念是以數的概念為基礎的，也就是説先得有數，然後我們才能用數量去描述事物。

所以，説“數是對數量的抽象”是一句邏輯不通——即使在文理上也不通——的謬論。

再看這句：“增加計數單位的概念：個數和順序的計量單位。”

“個數和順序的計量單位”是個什麼鬼表述？“‘個數’的計量單位是計數單位”？“順序”還有計量單位——其計量單位還是什麼計數單位？——嗎？

這都什麼跟什麼嘛？！

善意的去猜或者説幫他完善一下“個數”的表述如下：

計數單位是某數位上的數字幾所真實表示的幾個以該數位為計量單位的幾個計量單位中的計量單位。

我去~~~費勁！話怎麼説都不通，説明過於反常。

反常即有妖！

以下是捉妖記。

二、“計數單位”的概念是荒謬的、進入教材是誤人子弟的

1、“數”是沒有單位的

“數”是什麼？“數”是表示事物多少這一屬性的抽象概念。

“單位”是什麼？“單位”是表示事物的量的基本單元，這個基本單元對應着我們為度量事物的量而規定的量詞。

將表示事物多少的“數”與表示事物的量結合起來，我們就可以表示事物的“數量”了。

比如説，一片樹林中的樹木的量，如果以棵為基本單元即度量的量詞，我們就先以一整棵樹為1進行數數，數出來的數，加上量詞棵，比如100棵，就表示這片樹林中樹木的以棵為基本單元計量的數量是100棵。如果一個大的區域有好多片樹林，我們計量這個區域的樹林的多少，我們以片為基本單元計量即以片為計量單位，我們熟熟，比如數出來是18，我們就説這個區域有18片樹林，其中，18是數，片是量且是該量的單位。

那麼，“數”有單位嗎？沒有的！

2、“計數”抑或“記數”？將“記數”混淆為“計數”是一個本質性的錯誤

將一個數表示出來叫“記數”。

“記數”的方法——某種數字以及以這種數字按一定的規則進行組合以表示事物多少（後來從中抽象出“數”的概念）的方法——即“記數法”。世界上各個民族的初民們發明了各種各樣的記數法，當前世界通用、我們學的這種記數法是以阿拉伯數字（1、2、3……9，其實是古印度數字，甚至有可能是古中國用過的數字或者可能是古印度在古中國某種數字上經過改進而來的數字）按一定規則（“十進制”和“數位制/位值制”）進行組合表示數的方法。

對多少用數這個概念去描述並計量——對應着各種計（量）數的方法即計數法（比如，生物學中的平板菌落計數法）——叫“計數”也即計算（量）數量。

計數總是對應着具體事物的量，撇開量而單獨提計數是沒有意義的。

教材中學習“大數”的這一部分內容，本質上應該是大數的表示方法——數的書寫法和數的讀法，也即“記數法”。

故而説，將“記數”混淆為“計數”是一個本質性的錯誤。

所以，“計數單位”的概念是荒謬的，進入教材是在教錯誤的數學或者説錯誤地教數學，是誤人子弟的。

三、“計數單位”謬誤是如何產生的呢？

“計數單位”這個荒謬的概念究竟是如何產生的呢？以下我作些猜想。

既然是猜想，那就不是演繹推導出來的結論，而只是在有限事實/現象基礎上“（本質）直觀”（胡塞爾意義上的）到的“本質”。那就直接先端出我的猜想，然後對其作一番解釋説明。

我的猜想是：

“計數單位”這個稱謂/名詞是【（企圖兼顧阿拉伯數字記數法與中國漢字數字記數法）並/或（囿於且惑於現代慣常性地出於因利乘便的緣故而將阿拉伯數字與漢字數字非法組合）來書寫數的方式而生造出來的（一個四不像的且因此不能達到預期的二者兼顧之目的）的】偽概念。（抱歉，這句話比較長——有點康德內味，“【】”與“（）”是為了提示斷句/便於理解而加的記號）

以下對其作些解釋説明。

（1）企圖兼顧到阿拉伯數字及其記數法與中國漢字數字及其記數法的知識但對兩套記數法的本質及其不和調和處認知不足從而生造了一個“計數單位”的概念以期給其一個圓滿自洽的解釋

阿拉伯數字及其記數法

阿拉伯數字：0、1、2、3、4、5、6、7、8、9

記數法核心：數位制/位值制，十進位制

數位制/位值制的意思即將數字放在不同的位置從而表示相應的數，從而將數字所在的位置叫數位，以將數字置於不同數位以表示數的記數規則就叫數位制/位值制。

比如35這個數，由於3在十位這個數位上故其實際表示/對應的數是30、5在個位這個數位上故其實際對應的數就是5，用我們的母語漢語來讀這個數就是“三十五”，用英語來讀這個數就是“thirty five”。至於發明這套數字及其記數法的古印度人/阿拉伯人是如何用他們的母語來讀這個數的我就不知道了，但肯定也是類似於漢語和英語這個讀法。我要説的其實是，阿拉伯數字及其記數法表示的數，其書寫方法與讀法是分離的/不一致的。

漢字數字及其記數法

漢字數字：一、二、三、四、五、六、七、八、九、十、百、千、萬、億

記數法：半數位制/半位值制，十進位制

比如“九千八百七十六”這個數，千、百、十是指明數位以界定其前面那個數字實際表示/對應的數（如“千”前面“九”的寫法，“千”是用來指明“九”是9000——不得已借用阿拉伯記數系統示意一下——的，沒有這個“千”那“九”就不能確定其表示/對應的數了，由於數位是要靠寫出“千、百、十”這些指明數位的數字，故而説其是“半數位制”——不完全/不徹底的數位制）——故而其絕不是所謂的“計數單位”，用我們的母語漢語讀這個數就是“九千八百七十六”，我們發現，漢字數字及其記數法表示的數，其書寫方法與讀法是一致的。

現代英語中用的是阿拉伯數字記數系統，其對數的讀法也依賴於其母語英語中原本有的表示數的數字如one、two、three、four、five、six、seven、eight、nine、ten、eleven……hundred、thousand、million、billion、trillion等等。但，其一，由於英語是拼音/注音文字，所以這些單詞可能並非數字而只是為了讀數而發明出來的為不同的數進行注音的單詞；其二，諸如hundred、thousand、million、billion、trillion這些數字——姑且認為是數字——也並非所謂的計數單位或者説被當作計數單位來用。

善意地揣測，課標制定者以及教材編寫者可能懷着將兩種記數系統的知識都兼顧到並且將漢語語境中實際應用中的數的表示法（寫法和讀法）吸納到教材中的良好願望，但兩種記數系統之間又有齟齬處需要調和——一個圓滿自洽的解釋，從而慌不擇路地或者未經深思地生造出了一個“計數單位”的偽概念。

（2）囿****於且惑於現代慣常性地出於因利乘便的緣故而將阿拉伯數字與漢字數字非法組合的“混合記數法”並自以為得計地生造出“計數單位”的偽概念且以為可以將這種非法組合合法化

在現代漢語語境的用法下，如600000這個的數確實慣常性地被寫成60萬這樣的形式。

但根據上文（1）中的分析，我們可以知道/判斷：

將600000或六十萬這個數，將兩種記數法結合來寫成60萬是非法的，因為這根本是兩套數字的記數系統。即使是“對讀法的書寫”（注意這個表述）也得寫成全漢字數字即“六十萬”才是合法的。

那60萬的實際用法又是因何緣故而被髮明並被廣為接受的呢？我的猜想就四個字：因利乘便。激發這個念想的可能是“六十萬”這樣的漢語對數的讀法。

既然諸如60萬這種表示法是非法組合，那如何給其一個解釋以使得這種組合在一般看來是合法的呢？就是生造“計數單位”這個偽概念了，將60萬中的“萬”解釋為“計數單位”。殊不知，數是沒有單位的（詳見前文第二節）。引入所謂的“計數單位”，反而將本來用“數位制”這個概念就能澄清並明晰表達對於大數的記數（書寫方法和讀法）的知識給攪和得混亂不堪了。

所以，“計數單位”是一個蹩腳的、搗亂的、荒謬的偽概念。

四、數位與數級的區別與聯繫

數位指的是記數法（側重於書面地表示即書寫一個數的方法）中的一個記數規則。

數級指的是讀數法中的一個讀數規則。

數位側重於書寫/文字，數級側重於口讀/語言。

數位是記數法中規定的不變的規則，數級是雖有約定俗成的規則可從但又並非一定之規而是可因利乘便而變的。數級要借用數位來界定。比如我們在母語漢語環境下常用的四個數位一個數級的萬級、億級，億級以上的數級——如果還説或者還用數級來界定的話——就沒有什麼一定之規了，比如萬億，如果按四個數位一個數級的話那萬億就該換名了——這意味着漢字數字中要增加或者説再發明一個表示萬億這個數的獨立的數字（諸如“兆”、“京”之類的），而描述超級計算機運算速度每秒浮點運算多少次的億、億億、億億億就更沒什麼數級之規了。

不同語言環境——比如漢語和英語——下，對同一套記數系統比如阿拉伯數字記數系統來説，數位對於二者都是一樣的、不變的、均須遵從的，但數級卻是可以——實際上也確實是——不同的。漢語中的萬、億是常用數（以古人的生產生活中能涉及到的最大的數的界限來説）之讀法的數級——以四個數位為一個數級。英語中的thousand、million、billion、trillion是其常用數之讀法的數級——以三個數位為一個數級。

（多説一點，在英語文獻中看到的大數總是帶着小蝌蚪——從低數位到高數位每三位加一個小逗號，如此標記只是便於其用其三個數位一個數級的讀數法進行讀數，而在中文文獻中出現的大數如果帶這個三個數位一個的小蝌蚪，就有點不倫不類了——因為我們的讀數法是四個數位為一個數級的故而用不到這個小蝌蚪。）

關於數級，再極而言之地舉個例子或者説來個暴論：

123456789這個數，拋開數級，用漢語直接讀成“一億二千萬三百萬四十萬五萬六千七百八十九”或者間隔用“又”或“有”（這是中國古人就用的方式）作一番修飾而成“一億又二千萬又三百萬又四十萬又五萬又六千七百八十九”，在本質上來説，也未嘗不可。

精簡便捷——或者乾脆説偷懶——的念想是古今之人同一的，引入數級的概念及其規則，讓讀數變得更方便也更易於理解了。

所以啊，偷懶是人類進步的源動力——至少是之一；關鍵是，偷懶也得講究基本法——科學。

五、破而後立，談談如何更好地編寫及講解“認識大數”

嚴格説來，識數這一部分內容應該作為一個整體——將十以內的數、十到一百的數以及所謂大數連貫在一起——在一年級上學期就完整，而不應該根據所謂的兒童的理解能力將本來應為一體的內容切割成一段一段的分散到各個年級去教學。

舉例説，現行教材直到四上的認識大數這部分內容才正式講“數位”的概念，而前面講的10及以上、100以內的數難道不是因為有了數位才有這樣的數（的書寫形式）嗎？

所以，識數這個作為整體部分的內容應該以自然數的發現/發明——涉及到數字的創造、記數法（其中就包括數位制和十進位制）的創造——為線索，將各個數段的數包括大數自然而然地帶出來並認識，因為所謂的大數並非因為其大而不容易理解，而是大數是記數法確立後，大數——實際上是無論多大的數——就根據記數法而表示/創造出來了。發明記數系統的古人在實際應用中可能永遠接觸不到如萬億這樣的大數，但並妨礙他們在記數法的基礎上認識到有這樣的大數存在，也就是説，數作為一個抽象概念被建立起來了，並對自然數作為一個有無數個數的集合這樣的一個整體有了認識。

關於這一點，請參閲我對自然數如何被髮明的猜想的文章；

小學數學教-學探索｜作為概念的（自然）數是如何被認識到——發明和/或發現——的？一個猜想｜以重新發明數學的方式學習數學

但要對現行教材進行如此大刀闊斧的重編顯然是不可能的，那麼就只能在現有架構下作些修訂和打補丁的功夫了。

以下是我的建議：

1、補充講解完整的漢字數字及其記數法和阿拉伯數字及其記數法，其中尤其要講清楚記數法中的“數位制”和“十進位制”。

2、講清楚基於不同的數字及其記數法對數進行的書寫方法和讀法的不同，漢字數字及其記數法下其數的書寫方式與讀數方式是一致的，而阿拉伯數字及其記數法下其數的書寫方式與讀數方式是不一致的——其讀數方式根據不同的語言而有不同的讀法。

3、講清楚在不同語言下，讀數方法中的數級的分法是不一樣的，比如漢語對阿拉伯數字表示的數的讀法是四個數位一個數級而英語是三個數位一個數級；並且讓學生瞭解到，數級只是對常用數的讀法採取的一種因利乘便的、約定俗成的規則，對於很大的數，高數位的部分的讀法就根據各個語言中所發明的表示更大數的數字（比如漢字中的兆、京，等）來靈活地去讀了。

以下是對上述各條建議的補充説明：

第1條是重點，真正講清楚“數位制”後，“計數單位”的偽概念就可以清除掉了。

第2條的基礎上，就可以對實際使用中的諸如“60萬”/“600 thousand”這樣的表述形式作符合情理——但不合記數法的法理卻又因拗不過因利乘便的使用慣性而不得不妥協從而允許其正常使用——的解釋了，這種表述形式只是書寫方式上的便利形式，且其不影響我們讀取這個數的時候將其還原為正規的記數形式即“600000”。

第3條是為了讓學生了解為什麼要設立數級，設立數級便利了我們對於數的讀法，而且瞭解到了英語環境下數里面每三個數位加個“,”是個什麼意思、有什麼作用，也就明白了漢語環境下在數里面每四個數位加個“|”是什麼意思、有什麼作用，“,”與“|”都是有了數級概念後為了讀數的方便而加的標記。

六、結語

數學，數學，先有數然後才有關於數的學問即數學（算術、代數、數論等，即使是幾何這門討論圖形的學問，也多必須依賴於數）。

數的誕生即自然數的發明——人類認識到的第一類數就是自然數——是數學之開端。搞清楚——哪怕是猜想——自然數是如何被古人創生（發明或發現）出來的，或者從發明自然數的層次和視角方面去組織人類積累的關於自然數的知識，這才是真正的數學第一課——識數。

入門須正，境界要高。

數學第一課對於學好數學尤其是小學數學至關重要。

跋

略（參見原文）