對中國漢字數字記數法和阿拉伯數碼記數法的發明細節之探析-猜想，過五關斬六將_風聞

**按：**本文節選自“作為概念的（自然）數是如何被認識到——發明和/或發現——的？一個猜想”的註釋（註釋4、註釋6），因感覺其重要（數學第一課是識數，而識數的前提和基礎就是記數法），故特單獨將其成文，希望對有心者有所啓發和裨益。

無論是中國漢字數字記數法還是印度-阿拉伯數碼記數法，現在都是我們日用而不自知的知識，並且我們也沒有認真仔細的學習過這方面的知識。

學懂記數法其實是真正識數的基礎和關鍵。如何才能更好的學懂呢？沒有比與古人一起發明創造它更好的方式了。但古人沒告訴我們他們是如何發明的，所以，我們唯有猜想。

以下，隨我的猜想與古人一起發明記數法。

一、中國漢字數字記數法

中國的漢字數字記數系統以“一、二、三、四、五、六、七、八、九、十、百、千、萬、……”這些有限的基本數字按“十進制”和“位值制”——合稱為“十進位值制”（“十進制”的是否就必然是“位值制”的？我不太確定。下文分開討論）——的規則進行組合的方式來表示所有的數，這種表示“數”的方式即我們現在所稱的記數法。

這套記數法從發明到成熟經歷了數千年的漫長曆程。甲骨文時期之前現在還不可考，所以其發明只能通過甲骨文來推測重演，其成熟在篆文時期，至隸書（其創始在秦朝）時已幾近於今天的樣態。

以下分別通過甲骨文、篆文中所記載的“數”以及今人對“數”的讀寫方式來考察、認識這套記數法。

1、甲骨文中的記數法

我們先通過甲骨文來推測並重演這套記數法是如何發明出來的。

由於甲骨文時期古人還未抽象出“數”的概念故而還沒有“數”之觀念——“數”這個文字在甲骨文和金文中都沒有（發現）而是始見於戰國文字，所以，甲骨文中的在我們今天看來已算是“數”的“數”還不能稱之為“數”，而只能稱之為“多少”。

**（1）****用“**一~十”的“數字”表示“一~九十九”的“數”

甲骨文時期之前（可能“前”到以千年計）的某個時期的中國古人在發明出了表示“一、二、三、四、五、六、七、八、九、十”這十種“多少”（即“數”）的基本符號（即“一~十”這十個“數”/“數字”）之後，要繼續表示比“十”還“多”的“多少”（即比“十”還大的“數”）就存在兩種方案，一種是繼續發明更多新的符號，另一種是基於精簡原則就用這有限的十個基本符號去表示比“十”還“多”的“多少”（即比“十”還大的“數”），智慧的中國古人選擇了後一種。

甲骨文：一、二、三、四、五、六、七、八、九、十

那如何用“一~十”這十個基本符號去表示比“十”還“多”的“多少”（即比“十”還大的“數”）呢？

先看比“十”這種“多少”還再“多”“一”的這種“多少”（即“十”加“一”之後的“數”），如何去表示它呢？智慧的中國古人在深思熟慮之後發明了第一招。

第一招，單體符號組合**。**

就是將“十”和“一”這兩個符號組合起來去表示比“十”還“多”“一”的這種“多少”。

在古人由上到下、從右至左的刻寫習慣下，“十”與“一”的組合有四種形式：

第一種，“十”上“一”下（按我們現在從左到右的習慣，就是“十”在“一”前/左）；

第二種，“十”下“一”上（按我們現在從左到右的習慣，就是“十”在“一”後/右）；

第三種，“十”與“一”的合體（合文），即“一”在“十”上/內。

其中，第三種的“合體/合文”的形式容易與單體的“七”（形似現在的“十”）混淆，不妥當，放棄。第二種形式不合於解讀習慣，即按刻寫的順序依次來讀，不妥當，放棄。第一種形式沒有什麼問題，也只剩下這一種形式了，只能採取它。

於是，比“十”這種“多少”還再“多”“一”的這種“多少”（即“十”加“一”之後的“數”）就表示為“十一”了。

依此類推，十二、十三、十四、十五、十六、十七、十八、十九就順理成章的表示出來了。

為了防止“十四”這樣的由兩個單體符號組合表示的一個“多少”（即：一個“數”）被誤認為分別是兩個單體符號表示的兩個“多少”（即：兩個“數”），有時會在該組合的兩個單體符號之間加一個“有”或“又”字。

        

甲骨文：十七、十四（寫作“十有四”）

再繼續表示比“十九”“多”“一”的這種“多少”時，難題和困擾又來了。

於是，在尋求解決難題和困擾的方案過程中，智慧的中國古人發明了第二招。

第二招，十進制。

比“十九”“多”“一”的這種“多少”怎麼去表示呢？“九”“多”“一”就是“十”了，那就有兩個“十”了。

就用“兩個‘十’”去表示比“十九”“多”“一”的這種“多少”嗎？那如何賦予這“兩個‘十’”以表示比“十九”“多”“一”的這種“多少”的意義呢？或者説，如何理解將比“十九”“多”“一”的這種“多少”表示為“兩個‘十’”呢？

因為可以另外發明一個新符號去表示（如瑪雅文明記數法中的“二十進制”那樣：1-19的數都是用表示1的點“•”和表示5的槓/橫線“——”的組合形式來表示的，20的表示就要另外發明一個新符號“略”並將之與表示1的點“•”組合——即“1個20”，表示40就是用這個新符號與表示2的兩個點“••”組合——即“2個20”），但智慧的中國古人沒有選擇”這個發明新符號的方案，而是堅持“精簡原則”用既有的“一~十”這十個符號來表示。

既然是滿“十”了就用這個“十”與原有的“十”組合去表示比“十九”“多”“一”的這種“多少”，那也就意味着每滿一個“十”，新的“多少”的表示形式中就多“一”個“十”，那就是“滿十進一”（在這裏還不太明顯，在後面對“五十、六十、七十、……”的表示中就很明顯了）了。

於是，智慧的中國古人確立了“十進制”。

“十進制”既已確立（意味着對“兩個‘十’的組合”的表示形式賦予了意義和理解/解讀的規則），那就可以用“兩個‘十’的組合”去表示比“十九”“多”“一”的這種“多少”了。

那這兩個“十”如何去排列呢？有兩種形式可選：

第一，兩個“十”一上一下排列；

第二，兩個“十”左右並列排列。

第一種顯然不可取，因為會太長導致佔位置太多，而且再多幾個“十”的時候就會更長以至於刻寫載體都刻寫不下了，所以甚為不妥，放棄；第二種似乎合適，但有可能與單體的“八”混淆，更有可能使得左邊的那個“十”被混淆為左邊一列文字中的內容，所以得給這左右並列的兩個“十”加一點修飾使其變成“廿”這樣的形式，這樣它就只能被認作一個字了。

於是，比“十九”“多”“一”的這種“多少”就表示為“廿”了。

甲骨文：二十（“十”和“十”並列並加修飾）

比“廿”再“多”“一”就可表示為“廿一”了（“廿”在上、“一”在下，道理如前述，按習慣性的解讀順序排列，後文類似處不再另注）。

依此類推，繼續表示下去：

廿二、廿三、廿四、廿五、廿六、廿七、廿八、廿九。

比“廿九”“多”“一”的這種“多少”又該如何去表示呢？

首先，循規採用“十進制”；

其次，遵照將比“十九”“多”“一”的這種“多少”表示為“廿”的形式的道理和做法。

於是，比“廿九”“多”“一”的這種“多少”表示為“卅”（後面的“卌”同理）。

甲骨文：三十”、四十（並列“十”並加修飾）

與前述同理，繼續表示下去：

卅一、卅二、卅三、卅四、卅五、卅六、卅七、卅八、卅九；

卌；

卌一、卌二、卌三、卌四、卌五、卌六、卌七、卌八、卌九。

        

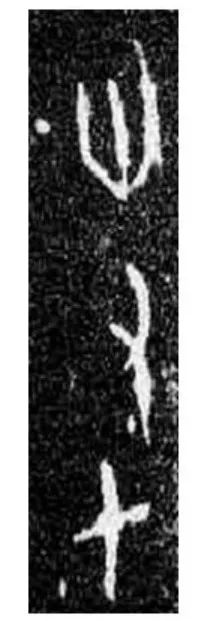
甲骨文：三十七、四十一

比“卌九”再“多”“一”就有/成了五個“十”了，難道要效法“廿、卅、卌”將其並列（加修飾）嗎？一來並列的“十”也太多了點導致佔的位置太寬；二來照此下去，後面要並列的“十”會越來越多導致佔位過寬，會寬到妨礙左右兩列的正常行文，同時也不便於識讀。

所以，繼續並列五個“十”（加修飾）的形式不妥當、不可取，需另謀良策。

而能用的又只有“一~十”這十個符號，故而可選的方案似乎是唯一的，即：

仿照“廿、卅、卌”將幾個單體符號糅合在一起變成“合體/合文”符號的形式，將“五”和“十”這兩個單體符號糅合在一起成為一個“合體/合文”符號的形式來表示比“卌九”再“多”“一”的這個“多少”。

甲骨文：五十

但這個“合體/合文”符號中的“五”已經不是表示“五”這個“多少”的“五”、“十”也已經不是表示“十”這個“多少”的“十”（注：合文符號中的數字“五”已經不是表示“五”這個“數”的“五”，“十”同理），那該如何賦予這個“合體/合文”符號形式的“五十”以意義或者説如何理解其中的“五”和“十”呢？

於是，智慧的中國古人經過苦思冥想發明了第三招。

第三招，位值制**（萌芽樣態）****。**

既然這個“合體/合文”符號形式的“五十”（其甲骨文形式如下圖）表示的是比“卌九”再“多”“一”的這個“多少”（即“五十”這個“數”），且是用來代替“並列的五個‘十’”的形式的，那就賦予“五”以“‘五’個/倍‘…’”的意義/意思，而這個“…”就是本該並列的那個“十”；或者可以這樣理解：“合體/合文”符號中的“十”就相當於一個“基數”，而其中的“五”就是這個“基數”的“個/倍數”。將此理解確立為規則，後面的同類“多少”的表示遵從此規則。

按此規則，後面就有“合體/合文”符號形式的“六十”、“七十”、“八十”、“九十”。

甲骨文：二十、三十、四十、五十、六十、七十、八十、九十

這個規則其實就是“位值制”（只不過在此甲骨文時期還處於萌芽樣態，但到了篆文時期就表現得非常明顯和成熟——因為篆文已沒有“合體/合文”而全部是單體的）。

這樣，比“卌九”再“多”“一”就表示為“五十”了（“十”在上。為什麼？或許沒什麼特別的道理，第一反應就是要這樣放）。

綜合運用前面的三招——遵循前述三大規則，“五十”之後的“多少”依次表示為：

五十一、五十二、……、五十八、五十九、六十；

六十一、六十二、……、六十八、六十九、七十；

七十一、七十二、……、七十八、七十九、八十；

八十一、八十二、……、八十八、八十九、九十；

九十一、九十二、……、九十八、九十九、十十。

        

甲骨文：五十六（寫作“五十有六”）、八十八

整體觀之，前文述及的“十進制”（“滿/逢十進一”）從“五十”起已表現得非常明顯。

（2）新創數字“百”以便利於表示“一百~九百九十九”的“數”

如果僅限於用“一~十”的符號，並按“五十、六十、七十、八十、九十”的表示形式之慣例，那麼比“九十九”再“多”“一”的這個“多少”只能用上下相連的兩個“十”的“合文/合體”符號形式來表示了。

這種表示形式是不妥當的：

第一，這個“合文/合體”符號要麼為了表示其是上下兩個“十”相連就必須刻寫得很長，這樣除刻寫費勁且不便外，也佔據位置過多，要麼就刻寫得稍長一些，這樣又容易與一個單獨的“十”混淆；

第二，若這樣表示，那後面會有三個“十”相連、四個“十”相連、五個“十”相連、……，這就長得連刻寫載體都容納不了了，更麻煩的是也難於解讀了。

即使不遵上下結構的“合文/合體”形式而採取左右結構的形式也不行，因為左右並列的形式已經被“廿”（即“二十”）、“卅”（即“三十”）、“卌”（即“四十”）用了，再用就會混淆了。

如何解決這個難題呢？在既有條件下，似乎沒有妥當的解決方案了。

因此，不得不創造一個新的符號（代替“兩個‘十’上下相連的‘合體/合文’符號”）來表示比“九十九”再“多”“一”的這個“多少”了。

於是，古人新創了一個符號：白（取其近似）。

甲骨文：白（取其近似）

“白”這個新創的符號對應於“‘十’個/倍‘十’”（相當於一個“基數”，也即我們現在所稱的“數位”），將它與“一”糅合成“合體/合文”就得到了“百”。

甲骨文：一百（寫作：百。“一”與“白”的“合體/合文”）

這個“百”中的“一”表示“‘一’個/倍‘白’”（即“基數”“白”的個數，也即以“白”這個“數位”來定的“一”所實際對應的“數”——100），也即“一”個/倍的“‘十’個/倍‘十’”。

如此，比“九十九”再“多”“一”的這個“多少”就表示為“百”（“一白”，也即“一百”）了。

與“百”同理，將二、三、四、五、六、七、八、九分別與“白”寫成“合體/和合文”就分別表示“‘二’個/倍‘白’”、“‘三’個/倍‘白’”、……、“‘九’個/倍‘白’”也即“二百”、“三百”、……、“九百”。

甲骨文：二百、三百、四百、五百、八百

有了“百”這個新符號，按“單體符號組合”、“十進制”和“位值制”三大表示規則，繼續表示“百”後面的“多少”。

甲骨文：(一)百(一)十四、(一)百六十、二百六十九、四百五十一、五百(一)十

甲骨文：一百九十九（寫作：百有九十有九）、二百零九（寫作：二百有九）、三百四十八（寫作：三百又卌八）

以下表示中帶下劃線“    ”表示“合體/合文”，“有”或“又”是甲骨文中表示前後兩個符號是一個組合內的以避免混淆。

百有一、百又二、……、百有八、百又九、百十；

百十一、百十二、……、百十八、百十九、百廿；

百廿一、百廿二、……、百廿八、百廿九、百卅；

百卅一、百卅二、……、百卅八、百卅九、百卌；

百卌一、百卌二、……、百卌八、百卌九、百五十；

百五十一、百五十二、……、百五十九、百六十；

百六十一、百六十二、……、百六十九、百七十；

百七十一、百七十二、……、百七十九、百八十；

百八十一、百八十二、……、百八十九、百九十；

百九十一、百九十二、……、百九十九、二百；

二百又一、二百有一、……、二百又九、二百十；

二百十一、二百十二、……、二百十九、二百廿；

二百廿一、二百廿二、……、二百廿九、二百卅；

二百卅一、二百卅二、……、二百卅九、二百卌；

二百卌一、二百卌二、……、二百卌九、二百 五十；

二百 五十一、……、二百 五十九、二百 六十；

………………………………………………………………………

九百 九十一、……、九百 九十九、十百。

（3）新創數字“千”以便利於表示“一千~九千九百九十九”的“數”

比“九百 九十九”再“多”“一”，按“十進制”和“位值制”的表示規則：

第一步，末尾的“九”“多”“一”則為“十”，“滿十進一”，新得“一”個“十”；

第二步，新得的“一”個“十”與已有的“九”個“十”（即“九十”）相加得“十”個“十”，“十”個“十”即為“百”，滿十進一，新得“一”個“百”；

第三步，新得的“一”個“百”與本有的“九”個“百”（即“九百”）相加得“十”個“百”。

那麼，比“九百 九十九”再“多”“一”所得的“十”個“百”就表示為“十百”嗎？

就其自身來説，規則上是合規的，形式上也適當。

但若如此表示，那後面的“十一百”（即“‘十一’個/倍‘百’”）就雖然合規但形式上就不妥當了。

而且既然“‘十’個/倍‘十’”已經發明瞭新符號“百”/“白”來表示，那麼“十”個“百”也需要發明一個新符號去表示並代替“十百”。

於是，古人新創了一個符號：千**。**

“千”這個符號在形制上與“百”類似，是“一”與“千”的“合體/合文”並從中減省掉一個橫即“一”，它既表示“千”又表示“一千”。

同理，“二千”、“三千”、“四千”就是“二”、“三”、“四”分別與“千”的“合體/合文”並從中減省掉一個橫即“一”。

“五千”就是“五”與“千”的“合體/合文”並從中去掉“千”本有的那個橫即“一”，或者説是用“五”取代“千”中的那個“一”。

“六千”、“七千”、“八千”、“九千”則不然，因為“六”、“七”、“八”、“九”在形式上（筆畫的相似度）與“千”接近，“合體/合文”的區分度和解讀性都不太好，所以不再採取“合體/合文”形式，而是以兩個單體形式的“六”與“千”以組合形式來表示“六千”，“七千”、“八千”、“九千”同理。

甲骨文：（一）千、二千、三千、四千、五千、七千

有了“千”這個新符號，按“單體符號組合”、“十進制”和“位值制”三大表示規則，繼續表示“千”後面的“多少”。

甲骨文：二千六百五十

以下表示中帶下劃線“    ”表示“合體/合文”，“有”或“又”是甲骨文中表示前後兩個符號是一個組合內的以避免混淆。

千有一、千又二、……、千有八、千又九、千有十；

千有十一、千又十二、……、千有十九、千又廿；

千有廿一、千有廿二、……、千有廿九、千又卅；

千又卅一、千有卅二、……、千又卅九、千有卌；

千有卌一、千又卌二、……、千有卌九、千又五十；

千又五十一、……、千又五十九、千又六十；

……………………………………………………………………

千又三百又一、……、千有三百有九、千又三百十；

……………………………………………………………………

千有九百 九十一、……、千有九百 九十九、二千；

二千又一、二千有二、……、二千有九、二千有十；

……………………………………………………………………

九千 九百 九十一、……、九千 九百 九十九、十千。

（4）新創數字“萬”以便利於表示“一萬~九萬九千九百九十九”的“數”

與將“十百”用新創的符號“千”來代替以表示比“九百九十九”再“多”“一”的這個“多少”同理，古人新創了一個符號“萬”代替“十千”來表示比“九千九百九十九”再“多”“一”的這個“多少”。

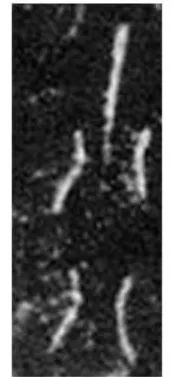
甲骨文：萬（其繁體字形：萬）

有了“萬”，就可以表示更多的“多少”（即“數”）了。

按“單體符號組合”、“十進制”和“位值制”三大表示規則，理論上可以從“萬又一”一直表示到“九萬九千九百九十九”（即從10001~99999）。

但古人在實踐中與之打交道的事物的“多少”還十分有限，故而在甲骨文中已經發現的最“多”的“多少”（即最大的“數”）是“三萬”。

 

甲骨文：三萬（甲骨文中發現的最大的“數”）

2、篆文中的記數法

我們再通過篆文來考察、認識一下成熟樣態的漢字數字記數法。

甲骨文中表示“多少”的圖形符號到篆文時已發展為成熟的文字符號，且由於篆文時期時古人已從用篆文文字符號表示的“多少”中抽象出了“數”的概念並隨之有了“數”之觀念，故而我們將用篆文文字符號表示的“多少”稱為“數”，而將表示“數”的文字符號稱為“數字”。

篆文中的用數字表示的數已基本沒有甲骨文中的“合體/合文”的形式（僅有“廿、卅”——或還有其它的——保留了下來），而全部是單體數字的組合。

小篆/秦古隸（雲夢睡虎地秦墓竹簡）：二千二百。簡上還有：二百廿

可見，篆文所記之數除了字形不一樣之外，其樣態已與今文（現今日常所用的漢字簡筆字）所記之數非常一致。

所以，接下來我們通過今文繼續考察、認識我們的漢字數字記數法。

3、今文**（漢字簡筆字）**中的記數法

我們現今日常所用的數字與甲骨文時期基本一致，僅多了一個數字“億”：

一、二、三、四、五、六、七、八、九、十、億。

數字“億”始見於篆文（大致年代在周初或春秋時期），至於其究竟表示的是什麼數或者説多大的數，要看其在多大的數範圍內或者説在什麼級別的數上。

據東漢時期徐嶽編撰的《數術記遺》記載：

黃帝為法，數有十等，及其用也，乃有三焉。十等者，億、兆、京、垓、秭、穰、溝、澗、正、載。三等者，謂上中下也。其下數者，十十變之，若言十萬曰億，十億曰兆，十兆曰京。中數者、萬萬變之，若言萬萬曰億、萬萬億曰兆、萬萬兆曰京。上數者數窮則變，若言萬萬曰億，億億曰兆，兆兆曰京也。下數淺短，計事則不盡，上數宏廓，世不可用，故其傳業惟以中數耳。

我的觀點是：

第一，人類在領會到數之無窮之前，所記之數包括其計算都與實踐中打交道的事物的多少密切相關，而實踐中所打交道的事物的數量是有限的，故而用不着太大的數去表示，因此“萬”以上的數字如“億、兆、京、……”最初發明時是按“十進制”的，即所謂“……十十變之……十萬曰億，十億曰兆，十兆曰京”；

第二，人類在領會到數之無窮之後，對於表示大數就產生了需求，再去發明新的數字就比較麻煩，也會因為數字太多而凌亂，加之記數法中的“位值制”已發展成熟（下文詳述），故而可以借用已經發明的“億、兆、京、……”這些數字來表示大數，只要將其數位/數的等級提升一下即可，即所謂“中數者、萬萬變之，若言萬萬曰億、萬萬億曰兆、萬萬兆曰京”，雖然還是“十進制”，但由於記數法中“位值制”的明顯、成熟和易於解讀，“億、兆、京、……”的數的等級就易於識讀了。

我們來看一個用今文的漢字數字記數法表示的大數（處於《數術記遺》中所載“黃帝為法”中的“中數”等級，我們現今也是按這個“中數”之法來記數的）：

九千九百九十九萬九千九百九十九億九千九百九十九萬九千九百九十九

這是這個數的寫法，那這個數是多少呢——也即怎麼識讀/讀數呢？

很簡單，直接按所記數字讀出來就可以了（每個字的發音發出來即可）：

九千九百九十九萬九千九百九十九億九千九百九十九萬九千九百九十九

也就是説，我們的漢字數字記數法是“讀寫統/同一”的。

而我們現今普遍採用的印度-阿拉伯數字/碼記數法是“讀寫不一致”的。

其記法：9999999999999999

其讀法：先由右至左從低位到高位挨個點過去辨識數位，確立了數位以後，還得給其加個分級標記（漢語的習慣是“四個數位一個數級”，英語德語法語等西語的習慣是“三個數位一個數級”），繼而確立讀法的中心數位（按漢語習慣，這個數的讀法的中心數位是“億”），然後才能按已經辨識出的數位從高位向低位依次讀過去。

“讀寫統/同一”是漢字數字記數法相比印度-阿拉伯數字/碼記數法的一項巨大優勢，恐怕也是我們的祖先在印度-阿拉伯數字/碼記數法傳入中國後仍然堅持使用我們自己的漢字數字記數法的最主要的原因。

再來看一下漢字記數法中的“十進制”和“位值制”。

寫出“一~(一)十萬”的數如下表：

從中可以發現，“十進制”（滿/逢十進一）是顯然的。

至於“位值制”，則不那麼顯而易見，需要剖析一下，因為我們通常習慣了印度-阿拉伯數字/碼記數法中的位值制，就以它為標準來看其它的記數法，結果發現我們的漢字數字記數法所記之數從表面形式上看，根本不符合那個標準形式。

來看一個數，其記/寫法：一萬二千三百四十五

其中，只有數字“五”才對應於它所表示的數“五”，其它的數字盡皆不與其所表示的數對應，比如，數字“十”表示的並非其對應的數“十”，數字“四”表示的也並非其對應的數“四”，數字“十”和“四”是作為一個整體存在的，其中的“十”是作為“基數”存在的、“四”表示的是此“基數”的數量（個數或倍數），作為整體它就表示“‘四’個‘十’”或“‘十’的‘四’倍”也即“四十”（即40），“三百”、“二千”、“一萬”同理。

該數中作為“基數”存在的“十”、“百”、“千”、“萬”其實就是標識/標示各自前面的“四”、“三”、“二”、“一”所實際對應的數的“數等”（數的等級，我編的名稱）。

或者乾脆就可以説，該數中的“十”、“百”、“千”、“萬”就是各自前面的“四”、“三”、“二”、“一”的“數位”，只不過這些“數位”被明寫出來了，而不像印度-阿拉伯數字/碼記數法中那樣“數位”是隱藏在其書寫形式內的而要挨個清點辨識才能將其確認。

所以，如果非要以印度-阿拉伯數字/碼記數法中的“位值制"的形式為標準，那麼中國漢字記數法中的”位值制“可以稱為”半位值制“。

其實，中國漢字記數完全可以與印度-阿拉伯數字/碼記數在形式上也一致。

比如前述的數“一萬二千三百四十五”，可以寫成“一二三四五”，與“12345”在形式上一致。識讀“一二三四五”也完全可以與識讀“12345”一樣，先辨識數位，然後讀數。

而在中國古人發明的籌算術（其記載最早見於戰國文獻，但其發明時間應該早得多，我認為至少是在甲骨文中的記數系統發明後不久就被髮明瞭，因為既然已經用“具體的‘數’”——如果非要稱其為數的話——去認識事物了，那隨之就會產生計算的需求，就要發明計算之術）中，實際上已經實踐了“一二三四五”這種表示數的方法。

中國古人發明的籌算

其中的“位值制”顯而易見。

中國古人之所以未將漢字數字記數法從“一萬二千三百四十五”的形式“進化”為“一二三四五”的形式，主要在於其“讀寫統/同一”的巨大優勢（堅定的文化自信必須以對我們文化的深刻理解和領會為基礎）。

二、印度-阿拉伯數碼記數法

印度-阿拉伯數字/碼記數法用“1、2、3、4、5、6、7、8、9、0”這十個數字/碼採用組合方式和“十進位值制”（十進制+位值制）去表示所有的數。

其中，“0”是在“1~9”這9個數字發明以後很長時間才發明的，剛開始只是表示一個“空位”即“該位沒有相應的數字可以表示其意思故而‘空’在那裏”，後來為避免誤讀誤解，就用比如小黑點“●”填補這個“空位”，後來又改用小圈圈“◯”，直到古印度人真正領會了“空”或者叫“虛無”的本質和意義之後“0”這個數字才被髮明出來（主流看法如此）。

我們以假設該記數法是原生的為前提——這意味着所有的任何一個數都有待去認識併發明它的表示法——來考察、認識一下僅用“1、2、3、4、5、6、7、8、9、0”這十個數碼去表示所有的數。

首先，自然地，用作為數字的“1、2、3、4、5、6、7、8、9”可以表示作為數的“1、2、3、4、5、6、7、8、9”。

接着，我們來看比9多1的數（即9的“後繼數”）怎麼去表示。

由於9已經是單獨的數碼所表示的最大的數了，而且也沒有別的數碼可用——如果不新創的話，所以只能用既有的數碼通過組合的方式來解決這個困境了。

於是9的後繼數（即比9多1的數或者説9加1之後的數）就記為了“1●”。

其中的“●”是用來佔據空位的（最初是直接空位，“●”是過度形態，然後才是“0”）。

如何來理解這個“1●”呢？或者説，如何賦予這個“1●”以比9多1的數的意思呢？

首先，要導入“十”，確立“十進制”。

9加1後就滿十了，“滿十進一”，所進的“1”就成為“1●”中的“1”。

如果該記數法是原生的，則這時還沒有“十”這個數呢。那“滿十進一”及其中的“十”作何解呢？所以要先導入“十”。

“十”應可理解為手指個數。古人在用手指輔助對事物進行計數時，點過一輪全部十個手指可能就會作個標記（比如在地上畫個槓，或放個小石子），然後繼續從頭點手指，再點過一輪全部十個手指後就再增加一個同樣的標記（再畫一條槓，或再放一個小石子）。在此實踐中就能領會到“滿十進一”。

其次，引入“位值”、“數位”，確立“位值制”/“數位制”。

原來的9消失了，留下一個空的位置，“滿十進一”所進的“1”佔據了空位前面的位置。也就是説，只佔一個位置的9的後繼數用了佔據兩個位置的符號來表示。

“空”的這個位置的“空”就是表示什麼都沒有，或者説沒有數字能表示它。

“1”所佔據的位置的“1”可以看作全部十根手指頭的數量的一個整體（或者説以全部十根手指頭的數量為基數，“1”表示1個或1倍的基數），但“1”又明顯不等同於“十”（全部手指頭至少有9個了——9已是可表示的數了）。

所以，只有賦予在此位置上的“1”以“十”（全部手指頭的數量）的意義/意思，這個“1”才能代表“十”。而在此位置上的數字“1”與以數字1表示的“1”這個數相比，唯一的不同，僅僅是其位置。因此，“1”這個數字因其所在位置而實際表示“十”這個數。

於是，“位值”的觀念就誕生了（隨着數的位數漸多，“數位”的概念就被髮明出來了）。

這樣，9的後繼數就被表示為“1●”。

那“1●”的後繼數怎麼表示呢？

原來9所在的位置當9加1滿十進一而“消失”之後就成“空”——以“●”示意這兒還是/有個位置——的了，那“1●”再加1，這個1自然加到這個“空”的位置上，這樣，原本為空的位置現在有數字1佔據了表示1這個數。

於是“1●”再加1的數就表示為“11”了，左邊的數字1因其位值為十，所以表示1個十，右邊的數字1的位值就是數字原本對應的數即1這個數。

這樣，“1●”的後繼數就被表示為“11”了。

依此類推，隨後的後繼數依次表示為：

12、13、14、15、16、17、18、19

那19再加1後的數如何表示呢？

繼續採用前面確立的“十進制”，滿十進一，9變成十後進一個1然後自己消失讓這個位置又成“空”，進的這個1到了左邊的位置，加到這個位置本有的1上，於是這個位置變成2，這個2因其“位值”為“十”，所以實際對應的數是“兩個十”即“二十”。

於是19再加1後的數就被表示為“2●”。

“2●”再加1後的數與前述同理，表示為“21”。

按“十進制”和“位值”的觀念，隨後的後繼續依次表示為：

22、23、……、34、……、55、……、76、……、98、99

99再加1後的數如何表示呢？

按“十進制”，滿十進一，兩個9所在的位置都成“空”了，右邊的9滿十進的1進到了其左邊的9上，左邊的9也隨即滿十了，再進的1就沒位置了，所以，向左邊再拓展出一個位置來安放進的這個1。

於是，99的後繼數被表示為“1●●”。

其中的1因其位置而實際對應的數是“十個十”即“一百”，所以其“位值”就是“百”了。

之後的後繼數與前述同理，依次表示為：

1●1、1●2、1●3、……、1●7、1●8、1●9、11●；

111、112、113、……、117、118、119、12●；

……………………………………………………………………

1●2●3●4●、……、5●6●7●8●9、……、999999999

……………………………………………………………………

1●●●●●●●●●●●、……、12345678987654321；

……………………………………………………………………

隨着拓展出的位置漸多，根究“位值”的觀念發明了“數位”的概念，用以標識一個數中每個數字所佔位置的“位值”。

於是，“位值制”/“數位制”確立了。

佔據“空”位代替“●”的圈零符號“0”在以後也被髮明出來，並且逐漸被認識為與1~9一樣的數字（而不僅僅是一個佔位符號），並可參與運算。

依據“十進制”和“位值制”，用“1、2、3、4、5、6、7、8、9、0”這十個數字就可以表示所有的數了。

我們來看一個大數：

12345678987654321

這個數是多少呢？這就需要對其進行識讀——相當於解譯。

而此識讀又是因語言不同而大異其趣的。

因此，與漢字數字記數法“讀寫統/同一”的特點相比，印度-阿拉伯數碼記數法是“讀寫不一致”的——至少漢語、英語、德語、法語等語言讀該記數法記的同一個數的讀法就有較大的差異（漢語與西語之間有大異，西語之間也有小異），不知道用古印度語會是怎麼樣。

先以漢語來識讀這個數：12345678987654321。

第一步，辨識每個數字所在的數位。

從右至左、由低位向高位挨個位置清點過去，並隨清點而讀出數位：

個，十，百，千，萬，十萬，百萬，千萬，億，十億，百億，千億，萬億，十萬億，百萬億，千萬億，億億（萬萬億）

當然，按我們四個數位一個數級的方法和習慣，會讓辨識數位相對簡易一些。

第二步，確立讀取的中心數位。

確立了數位後，讀取時也不能每個數字與其數位都讀出來如這樣：

一億億二千萬億三百萬億四十萬億五萬億六千億七百億八十億九億八千萬七百萬六十萬五萬四千三百二十一。

當然，這種讀法應該也不算“錯”，只是麻煩和不變。所以得改進。

改進方式就是：確立單一數位（姑且如此稱之。比如“億”，而“千億”這樣就是複合數位了）中的最高位為讀數時的中心數位，然後圍繞這個中心數位來讀。

第三步，讀取該數。

比如這個數的最高單一數位是“億”，那就圍繞“億”來讀取這個數。

如這樣：

一億億貳仟叁佰肆拾伍萬六千七百八十九億八千七百六十五萬四千三百二十一。

或這樣：

一億貳仟叁佰肆拾伍萬六千七百八十九億八千七百六十五萬四千三百二十一。

這是用漢語來識讀這個數。

那若用英語如何來識讀這個數——12345678987654321——呢？

這裏不詳細展開，僅擇其要者説一下。

英語中每三個位置才有一個數位名稱，如“千”（thousand）往上跳了兩個數位後是“百萬”（million）、“百萬”（million）再跳過兩個數位後是“十億”（billion）、“十億”（billion）再跳過兩個數位後是“萬億”（trillion）。這個數位自然也就是其數級。

讀數時先將數級用“，”標記出來，如這樣：

12,345,678,987,654,321

然後按漢語讀數時圍繞“中心數位”讀取類似，讀出這個數：

twelve thousand three hundred and forty-five trillion and six hundred and seventy-eight billion nine hundred and eighty-seven million six hundred and fifty-four thousand three hundred and twenty-one

最後來一點暴論：

印度-阿拉伯數字/碼記數法中每個數位的名稱應該以該名稱也對應於相應的數為前提，也即是説，你得先有每個數位的這種讀法的數（如漢字數字記數中的“十、百、千、萬、十萬、百萬、千萬、億、……”既是數字又對應於具體的數）。

所以，用“1~9”這九個數字/碼來表示數的記數法應該是次生的而不是原生的。其源頭——在此基礎上加以改造而成“1~9”數碼的記數法——可能有兩個：一個是印度本土的某種符號的記數法，一個是中國的某種符號的記數法（尤其是中國籌算術中表示數的方法）。

原文參見：作為概念的（自然）數是如何被認識到——發明和/或發現——的？一個猜想