小學數學的習題教學也應“始於‘集郵’，終於‘思想’——‘基本原理’”-1.2_風聞

**轉按：**在小學數學的習題教學中，我們不能一味地帶着孩子們去“集郵”即認識題型並學習其對應的解題方法和技巧然後通過大量刷題去訓練出“條件反射”，而是還應該、也更應該引導孩子們去領會“思想”即數學的思維方式和思考方法——其具體體現為猶如物理學中的“最小作用量原理”類的“基本原理”。“始於‘集郵’，終於‘思想’”才能“技進乎道“，”技進乎道方能如庖丁解牛遊刃有餘”。“過程還原、切換視角、轉換表述”是以我自己的體會為基礎提煉出的“基本原理”之一。限於見識、水平，我提煉出的“基本原理”難免淺陋、偏狹，其表述也未必精當，歡迎高人批評指正。原文參見《“基本原理”之“過程還原、切換視角、轉換表述”（二）・技進乎道方能如庖丁解牛遊刃有餘丨以求學問之心講有學問之題論講題之學問》【其“（一）”參見：《“基本原理”之“過程還原、切換視角、轉換表述”（一）……》】，鑑於原文的字裏行間有很多以小號和低亮度文字所作的註釋，所以建議閲讀原文。

緒論**（版本二，修改了末尾幾段）**

題型及與其匹配的解法和技巧固然是紛繁的知識尤其是關於如何應對考題的知識的一次歸納，但此一歸納後的所謂“乾貨”仍然數量龐大，需要學生去記憶，且需要通過大量的刷題去重複和熟悉以期形成固定模式的“條件反射”——所謂的“秒懂”、“秒解”。且不説這需要學生耗費大量的精力，更難堪的是其效果或許並不能盡如人意，因為這種訓練最好的效果也只能保證學生可以解決經驗範圍內的問題——所謂的“舉一反三”也仍然是在經驗範圍內。這種“做題家”型的“學霸”之“霸”只不過是一種虛幻的“績優”，此非吾之所欲也。

“吾生也有涯，而知也無涯。以有涯隨無涯，殆已！”題目千變萬化，是為“無涯”，題型及與其匹配的解法和技巧始終只不過是有限的知識，是為“有涯”。

然則，怎麼破？

還得再歸納！歸納提煉出“基本原理”性的“道”，引導學生去領會此“道”，憑此“道”可以衍生出應對千變萬化之題的“技/術”即解題思路和方法技巧，如同庖丁解牛，技進乎道後方能以無厚入有間遊刃有餘。

庖丁為文惠君解牛，……砉然向然，奏刀騞然，莫不中音。合於《桑林》之舞，乃中《經首》之會。

文惠君曰：“嘻，善哉！技蓋至此乎？”

庖丁對曰：“臣之所好者道也，進乎技矣。……臣以神遇而不以目視，官知止而神欲行。依乎天理，……因其固然，……以無厚入有間，恢恢乎其於遊刃必有餘地矣。”

再以物理學為例來説明其中的道理。

物理學追求的目標之一是簡潔。物理學家的任務絕不是把每一個實驗事實編成表格讓人們記住，這是不可能完成的任務。正如皮埃爾·迪昂在《物理學理論的目的與結構》中所述：“人的心智面對不計其數的具體事實，每一個事實因由大量各種各樣的細節構成而錯綜複雜，沒有一個人能夠囊括和保留所有這些事實性知識，也沒有一個人能夠把這些知識傳達給他的同胞”。

物理學家的打開方式是用抽象的方法從大量的實驗事實當中歸納、總結，去尋找普遍、共有的東西，把一大堆複雜的實驗事實“壓縮”成簡單的命題，形成物理定律，從而大大減少對人心智資源的佔用。……

物理學的目標是掌握世間萬物的規律。可自然如此紛繁複雜，即便只關注其中相對不那麼複雜的“非生命體”[4]，面對的情形也足以讓人目眩。僅僅通過一次“壓縮”，從自然事實歸納為物理規律仍然是不夠的。……每一種都還會有一大堆物理定律，對人有限的心智依然是難以承擔的負荷。因此物理學家還要進行第二次“壓縮”，把所有這些定律濃縮成少數“原理”，只要掌握了這些原理，通過有規則和可靠的計算，就可以從原理中提取出需要的定律。比如掌握了費馬原理，那麼幾何光學中的各種反射、折射定律大都能夠從中獲得。

這種“壓縮”被恩斯特·馬赫稱為“思維經濟”，是物理學的目標和指導原則。自然界的複雜程度之高和人類認知能力之有限之間的終極矛盾，使得人類的物理學必然是一種“思維經濟”。物理學家的工作，就是從對一個個自然現象和實驗事實進行“集郵”開始，歸納總結為物理定律；再在對物理定律“集郵”的基礎上進一步抽象成為理論體系，最終用少數的幾條原理，通過可靠的規則和計算就能夠描述、解釋或者預測大多數自然現象，到這裏工作才算完成。

……

物理教育的終極目標是讓學生具備解決未知問題的能力，而這個能力的核心就是物理學的思維方式和研究方法。物理教育可以始於“集郵”，但最終應該終於“思想”。

——引自：始於“集郵”，終於“思想”

在小學數學的習題教學中，我們不能一味地帶着孩子們去“集郵”即認識題型並學習其對應的解題方法和技巧然後通過大量刷題去訓練出“條件反射”，而是還應該、也更應該引導孩子們去領會“思想”即數學的思維方式和思考方法——其具體體現為猶如物理學中的“最小作用量原理”之類的“基本原理”。

“技進乎道方能如庖丁解牛遊刃有餘”這個單元的主旨就是“始於‘集郵’，終於‘思想’”。

本單元將通過闡釋如下幾條“基本原理”來體現數學“思想”——數學的思維方式和思考方法——的“不可思議的有效性”（該表述化用了諾獎得主尤金·維格納“數學在自然科學中不合理的有效性”一文的標題——有些譯本將“不合理”譯為“不可思議”——以及其中觀點）及其普適性（其普適性不僅在於數學——用在數學習題的解答上只能算是“牛刀小試”，還在於自然科學領域；或者説，其普適性在於他們適用於或者説可應用於所有的科學研究）：

1、“過程還原（即：將前後兩個靜態情狀之間的動態過程還原出來）、切換視角（即：從專注前後兩個靜態情狀轉向審視其發生機理）、轉換表述（即：將問題逐步做等價轉換直到可以列算式的表述）”；

2、“以其‘不變’統合其‘變’”（即：先將問題情境中的“變”化的東西與“不變”的東西——這些東西通常是各種“量”或“關係”——探尋出來，繼而以“不變”為基礎構造相等或等價的關係——其表示形式通常是一個等式——並將“變”統合於其中）；

3、……

……

每條“基本原理”將作為一個專題安排若干篇文章來討論。

限於見識、水平，我提煉出的“基本原理”難免淺陋、偏狹，其表述也未必精當，歡迎高人批評指正。

導讀

本文繼續將“（一）”文中闡釋的“過程還原（即：將前後兩個靜態情狀之間的動態過程還原出來）、切換視角（即：從專注前後兩個靜態情狀轉向審視其發生機理）、轉換表述（即：將問題逐步做等價轉換直到可以列算式的表述）”這一“基本原理”——數學的思維方式和思考方法——推廣到更多其它類型的問題。

本文要討論的例題如下：

例一、小明有4盒餅乾，小華有3盒糖，小明的餅乾和小華的糖的總價值為100元。如果兩人互換一盒，則兩人各自的餅乾和糖的總價值相等。問：1盒餅乾多少錢？

例二、爸爸和小明同時從家步行去學校，爸爸比小明每分鐘多走10米，當爸爸到達學校時，小明離學校還有3分鐘的路程，當小明到達學校時，爸爸已經超過學校240米。問：小明家到學校的路程是多少米？

例三、有一盒玩具小球，分為四種顏色，每種顏色的小球各若干個。若：每人可任取1~2個球，且要保證有3人能取得完全一樣。問：至少需要幾個人去取？

建議先自己思考一下，然後再閲讀本文會有更深切的體會。

----------------------------------------

練拳不練功，到老一場空。——民間諺語

例一

​

小明有4盒餅乾，小華有3盒糖，小明的餅乾與小華的糖加在一起的總價值為100元。如果兩人互換一盒，則兩人各自的餅乾和糖的總價值相等。

問：1盒餅乾的價值是多少元？

不知道這道題該歸於什麼題型（“雞兔同籠”問題的變型？），且不管它是什麼題型，我們還是以“過程還原、切換視角、轉換表述”的“基本原理”為指引去思考並探索出解題思路，再次感受和體會“‘基本原理’的‘思想’”的普適性（普遍適用性）。

解題思路

我們先將前後兩種靜態情景描述出來。

情景一如下：

小明4盒餅乾，其合計價值 ？元

小華3盒糖，其合計價值 ？？元

小明的4盒餅乾盒小華的3盒糖的總計價值為100元

情景二如下（兩人的東西的價值相等即各為50元）：

小明有3盒餅乾和1盒糖，其合計價值為50元

小華有1盒餅乾和2盒糖，其合計價值為50元

切換視角（將相同部分單列出來）將情景二轉換表述為：

(1盒餅乾+1盒糖)+2盒餅乾=50元

(1盒餅乾+1盒糖)+1盒糖=50元

由此可知：

2盒餅乾與1盒糖價值相等

【接下來的思路可分兩種，以下“花開兩朵，各表一枝”】

【其一如下】

則

(1盒餅乾+1盒糖)+2盒餅乾=50元

可重新表述為（將1盒糖替換為2盒餅乾）：

1盒餅乾+2盒餅乾+2盒餅乾=50元

即：

5盒餅乾的價值為50元

故：

1盒餅乾的價值為10元（50÷5=10）

【其二如下】

再以此“知”來重新審視情景一：

小明4盒餅乾，其價值 ？元

小華3盒糖，其價值 ？？元

？與 ？？合計為100元

易見，情景一可切換視角轉換表述為：

小明2盒糖，其價值 ？？元

小華3盒糖，其價值？？？元

？？與 ？？？合計為100元

此即：

5盒糖的總價值為100元

則有：

1盒糖的價值為20元（100÷5=20）

也即：

2盒餅乾的價值為20元

故：

1盒餅乾的價值為10元（20÷2=10）

答題表述

由題設可知：

3盒餅乾和1盒糖的合計價值為50元

1盒餅乾和2盒糖的合計價值為50元

由此可知：

2盒餅乾與1盒糖的價值相等

則：

“3盒餅乾和1盒糖”與“5盒餅乾”的價值相等為50元

故，1盒餅乾的價值為：

50÷5=10（元）

例二

爸爸和小明同時從家步行去學校，爸爸比小明每分鐘多走10米，當爸爸到達學校時，小明離學校還有3分鐘的路程，當小明到達學校時，爸爸已經超過學校240米。

問：小明家到學校的路程是多少米？

不知道這道題該歸於什麼題型（行程問題？），且不管它是什麼題型，我們仍然以“過程還原、切換視角、轉換表述”的“基本原理”為指引去思考並探索出解題思路，再次感受和體會“‘基本原理’的‘思想’”的普適性。

【這道題的題設表述有點不合情理：既然是“從家去學校”，那爸爸到達學校後為什麼不是停下來而是還要繼續走以至於“超過學校240米”呢？合情合理的情境設計可以是這樣：爸爸和小明同時從家步行去學校，爸爸比小明每分鐘多走10米，爸爸在途中繞道去書店給小明買了個文具，由於繞道多走了240米、耗時3分鐘，結果爸爸與小明同時到達學校時。】

解題思路

爸爸到達學校時小明還在離學校還有3分鐘路程的途中某位置，從該時間點開始計時的3分鐘內，小明從途中那個位置走到了學校，爸爸從學校走到了超過學校240米的某處。

由此可知，爸爸在3分鐘內所走的路程為240米。

則，爸爸的步行速度為每分鐘走80（240÷3=80）米

則，小明的步行速度為每分鐘走70（80-10=70）米

因此，在爸爸從家到達學校的時間內，爸爸比小明多走的路程為小明按每分鐘走70米的速度走3分鐘的路程，即210（70×3=210）米。

考慮這210米是如何“走”出來的：

這210米是每分鐘多走10米“走”出來的。

那麼，每分鐘多走10米，需要多少分鐘才能多“走”出210米呢？

顯然，是21（210÷10=21）分鐘。

而這21分鐘也即爸爸從家步行到學校所走的時間。

前已算得爸爸的步行速度為每分鐘80米

則小明家到學校的路程為：

80×21=1680（米）

驗算：1680÷80=21，1680÷70=24，24-21=3；無誤。

答題表述

由題設可知，爸爸的步行速度即每分鐘走的路程為：

240÷3=80（米）

則小明的步行速度即每分鐘走的路程為：

80-10=70（米）

則小明3分鐘所走的路程為：

70×3=210（米）

則爸爸從家步行到學校所走的時間為：

210÷10=21（分鐘）

則小明家到學校的路程為：

80×21=1680（米）

例三

有一盒玩具小球，分為四種顏色，每種顏色的小球各若干個。

若：每人可任取1~2個球，且要保證有3人能取得完全一樣。

問：至少需要幾個人去取？

不知道這道題該歸於什麼題型，且不管它是什麼題型，我們仍然以“過程還原、切換視角、轉換表述”的“基本原理”為指引去思考並探索出解題思路，再次感受和體會“‘基本原理’的‘思想’”的普適性。

【這道題是我討論完上面兩道例題後臨時找到的題（因為只討論兩道習題而且是相對不太難的題，似乎有點單薄，説服力不夠，故而臨時再找合適的習題來為這篇文章壓陣、增色）。更難能可貴的是，我之前沒有接觸過這道習題，也沒接觸過這類習題，所以，以下的解題思路，就是我寫這篇文章的此時此刻對這道題進行思考的即時而真實的記錄。】

解題思路

【胡思亂想……茫然呆滯……差不多五分鐘了吧，似乎有點想法了，其實是下定決心不怕麻煩要開始一步一個腳印地去探索了，也就是説，不再企圖能輕鬆想想就能洞察玄機而是要將細節推導出來，再從細節中去“發現”解題思路。第一步最難踏出去，但一定要踏出去，走錯了都比裹足不前要好。】

每人可任取1~2個球，且要保證有3人能取得完全一樣。

所問為至少需要幾個人去取，“至少”意味着“在最複雜的情況下”的結果，最複雜的情況是什麼情況呢？直覺應該是每人所取的為2個球且其顏色不同。那我們先來討論這種情況下所需人數。

【但此處尚有疑問。每人任取1~2個球，則其取法對應着3種情況：其一，每人取2個球且其顏色一致；其二，每人所取的為2個球且其顏色一致；其三，每人所取的為1個球。哪種情況下能使得“保證有3人能取得（de，輕聲）完全一樣”所需的人數是“至少”呢？是“最複雜的情況下”還是“最簡單的情況下”？如何判定“最簡單”和“最複雜”呢？“至少”究竟是什麼意思？是在某種情況下的“最多”還是“最少”？這些都尚存疑慮。疑慮雖有且多，但無論如何要走下去看看，看了才知道，不看永遠不知道。所以，暫時不管，先按直覺討論自以為的“在最複雜的情況下”的情形，完後再討論“其它情況下的情形。當然，之所以有這些疑慮，也有可能是出題人在這方面有疏漏：題設表述產生了歧義——即從中可以理解出與出題人原意不一致的意思。這個我們討論完各種情況後再來審視。】

為表述方便，我們假定四種顏色分別為：白、黃、紅、藍。

以下還原取球的過程：

第1人，白、黃

第2人，紅、藍

第3人，白、紅

第4人，黃、藍

第5人，白、藍

第6人，……

咦，這種組合是這個“最複雜情況下”的“最簡單組合方式”還是“最複雜組合方式”呢？我們要的結果即“所需人數‘至少’”對應着哪種“組合方式”呢？進而又想，是否“最複雜情況下”對應的不是“至少”而是“最多”呢？

這時的直覺，應該是“最簡單的情況下”可達成“所需人數‘至少’（這裏理解為‘最少’）”的結果。

那我們調整方向，先來討論“在最簡單的情況下”的情形。

哪種情況最簡單——以所需人數“最少”來衡量——呢？直覺是“每人各取1個球”的情況。

那我們先來討論“每人各取1個球”的情況的情形。那這種情況下，什麼樣的取球安排能使得所需人數最少呢？直覺是每4人為一個輪次，每個輪次中的4個人所取球的顏色各不相同——即4人各取1個顏色的球，因為假若每個輪次中的4個人取球有重複——即所取球的顏色相同——的話，那可以推而廣之，無論多少人來，都取相同顏色的球，那……

咦，又不對了：若有人取相同顏色的球，那豈不是所需人數就更少嗎？比如，極而言之：前3個人都取同樣顏色的球，那不就是“有3人取得（de，輕聲）完全一樣”了嗎？而這不就是“至少”了嗎？

不過，深思一下，這種情況下的“至少”是得不到“保證”的，是需要“運氣”的，而且是“狗屎運”——頭3個人就取了相同顏色的球。

所以，似乎有點明白題設中的“保證”是什麼意思了：不能把“至少”交給運氣，而是要擯棄一切運氣（機緣巧合），也就是説，要考慮“最不利”（也就是最極端/惡劣）的情況下所需的人數，這樣求得的人數才是有“保證”的“至少”。

那兜了一圈，又回到要先討論“在最複雜（“最不利”意味着“最複雜”吧）的情況下”的情形了。

直覺“最複雜的情況”還是“每人各取2球且其顏色不同”，並且，這種情況下的“最不利”的情形是“每4人一個輪次且每個輪次中各人所取的球的顏色均互不相同即沒有重複（兩個球的顏色都一樣才算重複，只要其中有一個球的顏色不相同，就不算重複）”。

下面將取球過程還原出來：

第1人，白+黃

（直覺是：第1人取任意兩色均可，只要第1~4人所取不重複即可，下同）

第2人，紅+藍

第3人，白+藍

第4人，紅+黃

第5人，白+……

突然感覺這樣開列組合還是不妥，因為不容易看清是否會漏項，還是按將“白、黃、紅、藍”依次放在每個組合的前面一個比較容易識別。因為兩種組合情況（“顏色一+顏色二”與“顏色二+顏色一”）是等價的，所以每個組合中的兩種顏色哪個排在前面無所謂。

我們重新來排：

第1人，白+黃

（直覺是：第1人取任意兩色均可，只要第1~4人所取不重複即可，下同）

第2人，黃+藍

第3人，紅+白

第4人，藍+紅

第5人，白+藍

（發現前面的直覺有點不對，不是“只要第1~4人所取不重複即可”了，而是第1~？人所取不重複即可，至於“？”究竟是幾，待排下去方知。反正記住下面需要在確認“？”後做出調整即可）

第6人，黃+紅

第7人，紅、……

看不清了，不如畫個“連連看”的圖示來幫忙吧。

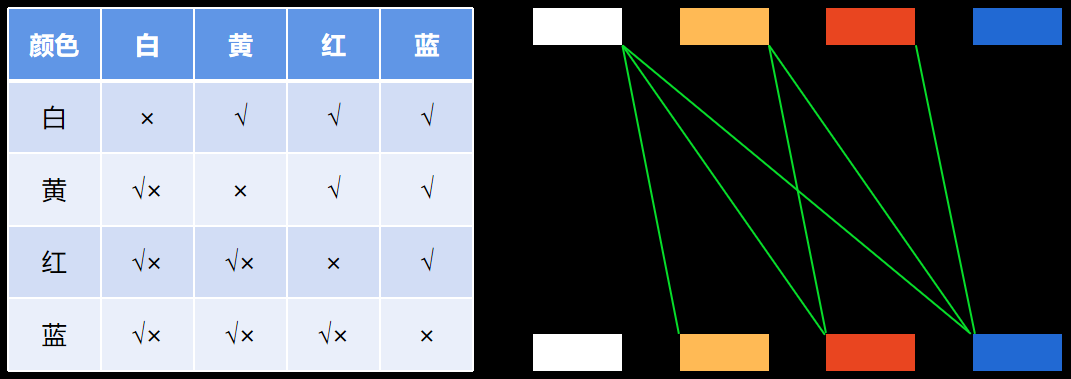
圖中左部和右部分別以不同的方式對四種顏色的組合進行了“遍歷”（計算機專業術語，可顧名思義，或百度查詢其意。簡單説：所謂遍歷——Traversal，是指沿着某條搜索路線，依次對樹/圖中每個節點均做一次訪問）操作，發現符合條件的（每個組合有兩種顏色且其顏色不同，組合之間兩兩不重複——組合內兩種顏色的兩種排列次序算一種組合）只有6種組合（圖中左部標記釋義：“×”表示由於兩種顏色相同所以組合“非法”，“√×”表示由於雖然顏色不同是合法的但因屬於重複而“違法”故而還是“非法”的，“√”表示是“合法”的組合），即：白+黃，白+紅，白+藍，黃+紅，黃+藍，紅+藍

由上圖可知，符合條件的組合只有6種，即：

白+黃，白+紅，白+藍，黃+紅，黃+藍，紅+藍

也就是説，取球時要每6人一個輪次且每個輪次內的6人所取的顏色組合不重複。

我們照此重新來排。

第1人，白+黃

第2人，白+紅

第3人，白+藍

第4人，黃+紅

第5人，黃+藍

第6人，紅+藍

【第一輪後，6個人所取的組合兩兩之間各不相同。】

第7人，白+黃

第8人，白+紅

第9人，白+藍

第10人，黃+紅

第11人，黃+藍

第12人，紅+藍

【由於組合僅有6種，所以第二輪後，已取球的12人必然分為6對——每對內的兩人所取組合相同。（第二輪中的6人所取的組合，其排列次序（即哪個人所取的哪個組合排在第幾人）無所謂——即不影響結果，只要這6人兩兩不同地取完了6種組合即可）】

第13人，……

我們發現，第13人（即第三輪次的第1人）取球時，雖然TA能取的組合是6種組合中的任意一個，但無論取哪一個組合，必然會與前兩輪中已有取到相同組合的兩人取到相同的組合，也就是説，到第13人取球后，必然會有3個人取到相同的組合也即題設所要求的“3個人取得完全一樣”。

所以，“在最複雜的情況下”（即：每人各取2個球且其顏色不同），“至少”需要13個人去取球才能“保證有3人取得（de，輕聲）完全一樣”。

接下來，為了驗證一下我們的“直覺”（即：“在最複雜的情況下”才符合題設意思及其條件，以及，“每人各取2個球且其顏色不同”就是“最複雜的情況”）是否正確，我們再來討論一下其它兩種情況下的情形。

先來討論“每人各取2個球且其顏色相同”的情況。

我們來排一下（即：還原取球的過程）：

【前面已討論過，每個輪次中取球的各人所取不同才能使得“有3個人取得完全一樣”是有“保證”的——即“是不需要靠運氣的”。所以，下面仍照此來排。】

第1人，白+白

第2人，黃+黃

第3人，紅+紅

第4人，藍+藍

【可以發現，組合只有4種，所以取法上是：每4人一個輪次且各人所取兩兩不同。】

第5人，白+白

第6人，黃+黃

第7人，紅+紅

第8人，藍+藍

第9人，白+白

第10人，……

我們發現，第10人（即第三輪次的第1人）取球時，雖然TA能取的組合是4種組合中的任意一個，但無論取哪一個組合，必然會與前兩輪中已有的取到相同組合的兩人取到相同的組合，也就是説，到第10人取球后，必然會有3個人取到相同的組合也即題設所要求的“3個人取得完全一樣”。

所以，在此情況下（即：每人各取2個球且其顏色相同），“至少”需要10個人去取球才能“保證有3人取得（de，輕聲）完全一樣”。

易知，在餘下的第三種情況下（即：每人只取1個球），也是“至少”需要10個人去取球才能“保證有3人取得（de，輕聲）完全一樣”（因為每人可取的也是4種顏色中的1個，故而與“每人各取2個球且其顏色相同”的情況下的情形是一致的）。

現在，還剩下最後一個疑慮需要討論，即：

“至少”——與“保證”緊密相關的——究竟是什麼意思？

“保證”如前所述應該還是意味着“不能倚賴於運氣”，也即需要考慮“最不利情況”，而“最不利情況”顯然是“最複雜的情況”。所以，“在最複雜情況下”的“至少”才是符合題意及其條件的“至少”。

故，滿足題設要求即“保證有3個人取得完全一樣”而“至少”需要的取球人數就是在“每人各取2個球且其顏色不同”的情況所“至少”需要的取球人數，即：13人。

現在我們來看看答案（這道題的來源的一個微信小視頻中視頻作者的解題方法及其結果）。

【我的習慣是，碰到未曾遇到過的新鮮類型的習題，總是堅持自主思考、獨立探索出解題思路之後，再去看習題的答案及其解法，其一是為了通過答案/正確結果驗證自己的解題思路及其解題方法是否有誤，其二是為了與答案中的解題方法（或常規的也即一般大家所教-學的解題方法）有何異同——相同或類似那是“英雄所見略同”、不同則意味着“發現了新大陸”。】

所討論習題的來源視頻及作者的解題方法。

作者將其微信視頻設置為“私密”，導致無法直接引用，故而只能截圖顯示。

愚見以為其講解是“不究竟”的，只講了“其然”而未講其“所以然”（清華小哥都不能免俗地滿足於“套路”、“技巧”——如其所授的口訣“極端情形再加1”——的炫耀式傳授的教-學方式，令人失望），這會導致原本就不會的學習者還是不會（原本會的自然就不需要向其學了）。這種“不究竟”的習題講解方式究其原因：其一，可能是“傳統”使然（詳參《小學數學“教-學”探索·習題篇：習題的思考與作答丨結語：請珍視這本難得一見的以授人以漁為旨歸的典範之作》一文第二節的相關論述）；其二，這種小視頻時間一般都很短——短至三五分鐘之內，在這麼幾分鐘的時間內是無法對思考方法（包括在思考情境中的心理、心情的波動。“思考”及其方法一定程度上也取決於性格修養）和解題思路的探索過程做出深入細緻的討論的。

對照作者給出的解題方和題目答案發現，我的答案是錯誤的，原因在於雖然解題思路在大方向上是正確的但未能克竟全功，具體説就是：沒有將已經想到的要考慮的是“在最不利情況下”（也即“在最複雜情況下”）的情形這個原則貫徹到底，僅僅將“最不利情況”定位到“每人各取2球且其顏色不同”的情況，而未能將“最不利情況”定位到“三種情況的綜合”（這三種情況在前述討論實際上都已經被識別出來了，即：“每人各取2球且其顏色不同”，“每人各取2球且其顏色相同”，“每人各取1球”）的情況。

【這個疏漏説明：我的“洞察力”還不夠，需要繼續訓練使其提升；或者，是我的“心性修養”還差了點火候（自以為破解了玄機時就自鳴得意了，結果“大意失荊州”，導致未能繼續往下深思一步），致使“為山九仞，功虧一簣”（不亦悲夫！），以後定當吸取教訓，戒驕戒躁，提升“心性修養”。】

以下繼續按照前述我們自己探索出的解題思路繼續往下走使其圓滿。

……

現在，還剩下最後一個疑慮需要討論，即：

“至少”——與“保證”緊密相關的——究竟是什麼意思？

“保證”如前所述應該還是意味着“不能倚賴於運氣”，也即需要考慮“最不利情況”，而“最不利情況”顯然是“最複雜的情況”。所以，“在最複雜情況下”的“至少”才是符合題意及其條件的“至少”。

故，滿足題設要求即“保證有3個人取得完全一樣”而“至少”需要的取球人數就是在“每人各取2個球且其顏色不同”的情況所“至少”需要的取球人數，即：13人。

最後，我們對已經作出的思考再作一番思考，審視一下其中有無疏漏、錯謬之處。

【也就是“思考（動詞）自己的思考（名詞）”，這是我曾經總結出來的一條經驗和體會，也是我經常告誡孩子的一點（我總是鼓勵/規勸孩子將她的思考過程書寫下來——哪怕是簡單的草稿，以備後續核查），但當時更多的目的在於發現自己錯了後能比較容易的核查到自己錯在什麼地方，看來，現在還得完善一下這條經驗和體會的功能，即：完成思考後還需以“對自己的思考再做一番思考”的原則去審視一下已經思考出的解題思路有無疏漏、錯謬之處。】

……【對自己的思考再行思考的過程，略】

咦，似乎不對啊：

既然是考慮“最不利的情況”（也即“最複雜的情況”），且題設條件是“每人可任取1~2個球”，“1~2個”啊，那意思是每個人既可以取1個球也可以取2個球啊，沒有必須每人都取同樣個數的球的要求或者説道理啊；進而想到，取2個球的情況下，也沒有必須是每人都是要麼取2個顏色不一樣的球、要麼取2個顏色一樣的球的要求或者説道理啊；這個“要求或者説道理”是我自己“臆測”的，在題設的題意及其條件中是沒有根據的，是我自己“會錯了意”。

所以，正確的“最不利的情況”（也即“最複雜的情況”）是：

“每人各取2個球且其顏色不同”、“每人各取2個球且其顏色相同”和“每人各取1個球”這三種情況之綜合的情況。

由前述分析已知：

“每人各取2個球且其顏色不同”的情況對應着6種組合/取法

“每人各取2個球且其顏色相同”的情況對應着4種組合/取法

“每人各取1個球”的情況對應着4種取法

則三種情況的綜合情況對應的組合/取法就有14（6+4+4=14）種。

我們來排一下（還原取球的過程）：

【排法：每14人一個輪次，每個輪次中的14人所取的球及取法組合兩兩之間各不相同。】

第1人，白+黃

第2人，白+紅

第3人，白+藍

第4人，黃+紅

第5人，黃+藍

第6人，紅+藍

第7人，白+白

第8人，黃+黃

第9人，紅+紅

第10人，藍+藍

第11人，白

第12人，黃

第13人，紅

第14人，藍

【第一輪後，14個人所取的組合兩兩之間各不相同。】

第15人，白+黃

第16人，白+紅

第17人，白+藍

第18人，黃+紅

第19人，黃+藍

第20人，紅+藍

第21人，白+白

第22人，黃+黃

第23人，紅+紅

第24人，藍+藍

第25人，白

第26人，黃

第27人，紅

第28人，藍

【由於組合僅有14種，所以第二輪後，已取球的28人必然分為14對——每對內的兩人所取組合相同。（第二輪中的14人所取的組合，其排列次序（即哪個人所取的哪個組合排在第幾人）無所謂——即不影響結果，只要這14人兩兩不同地取完了14種組合即可）】

第29人，……

我們發現，第29人（即第三輪次的第1人）取球時，雖然TA能取的組合是14種組合中的任意一個，但無論取哪一個組合，必然會與前兩輪中已有的取到相同組合的兩人取到相同的組合，也就是説，到第29人取球后，必然會有3個人取到相同的組合也即題設所要求的“3個人取得完全一樣”。

所以，“至少”需要29個人去取球才能“保證有3人取得（de，輕聲）完全一樣”。

【雖然在自主思考、獨立探索解題思路的過程中在大方向正確的情況下有所疏漏，未能克竟全功，但自己在思考過程中的獲得的經驗和體會彌足珍貴，這是真正屬於自己的東西，融進了我們自己的思維方式中，她（之所以用擬人化的稱謂，是因為我覺得這個“真正屬於自己的東西”是與作為人的我們自己融為一體了，是人的一部分，而且具有“靈性”；之所以用指稱女性的“她”，是受到了歌德在《浮士德》的終章寫下的那句名言的影響，其言曰：“一切過往的不過是象徵，那不美滿的在這裏完成，不可言喻的在這裏實行，永恆之女性，引導我們上升。”）將助益於我們以後對其它複雜而有難度的問題的思考及其解決思路/方案的探索；況且，“吃一塹長一智”，痛過更能體會深切——“人類總是以痛苦為代價領會真理”（復旦大學哲學院王德峯教授——已退休——的斷語）。】

答題表述

每人在放了4種顏色的球的一盒球中任取1~2個球，其取法總共有14種，具體是：

“每人各取2個球且其顏色不同”的情況下的6種取法

“每人各取2個球且其顏色相同”的情況下的4種取法

“每人各僅取1個球”的情況下的4種取法

則，要“保證有3個人取得完全一樣”所需的“至少”的人數是在如下情形下的人數：

以14人為一個輪次去取球，每個輪次中的14人的取法兩兩之間各不相同，也即每個輪次中的14人每人各用一種取法且不與他人的取法相同以保證將14種取法都採用一次且僅一次；兩個輪次之後，已經取球的28人中必然分出14對（一對為兩人）且每對中的2人的取法是相同的；第三個輪次的第1人也即總人數中的第29人取球時，無論其取法是14種的哪一種，都總是會與前兩個輪次後已有的某一對的取法相同，也即總有3人的取法相同。

因此，滿足題設要求即“保證有3個人取得完全一樣”而“至少”需要的人數為：

14+14+1=29（人）

答：至少需要29人去取。

【解決這個問題之後，我們可以從中總結出解決這一類問題的經驗：先判斷在何種情況下是符合要求的（本題是“最不利情況下”也即“最複雜情況情況下”，別的問題可能對應着不同的情況，總之，“推到極端”的“極限”——極而言之——的思想要貫徹其中），然後看這種情況下存在多少種“可能情形”（本題是“球的取法/組合方式”），繼而以“種數”為一個輪次，看看幾輪後的第幾人能滿足題設要求，最後算出結果。】

小結

從對上述例題的解題思路的探索中我們可以再次感受和體會到“基本原理”即“過程還原（即：將前後兩個靜態情狀之間的動態過程還原出來）、切換視角（即：從專注前後兩個靜態情狀轉向審視其發生機理）、轉換表述（即：將問題逐步做等價轉換直到可以列算式的表述）”作為指導“思想”——表徵數學的思維方式和研究方法——的普適性及其“妙用”。

在此感受和體會中，我們也更好地領會了“基本原理”中藴含的“思想”及其所表徵的一種數學的思維方式和研究方法，這就為我們思考和解決其它更多的問題奠定了堅實的基礎，更重要的是涵養了我們自主思考、獨立探索的勇氣和能力。

另外，我們也經歷了一次“模糊的探索”之旅及其其中的對於“心性修養”的考驗和磨鍊，這對於解決其它複雜而有難度的問題乃至於今後從事真正的科學或技術的研究都是大有裨益的寶貴經驗和體會，因為通過自主思考和獨立探索而獲得的這種經驗和體會將會融入我們的思維中，成為真正屬於自己的“默會知識”即“know-how”。

— 完 —

【其它相關文章以及後續更多相關文章請由原文鏈接按圖索驥。】