想嚐嚐“宇宙運行的規律”？那你高低得啃一口這個蔬菜_風聞

前段時間上映的國產電影《宇宙探索編輯部》，受到了很多觀眾的好評。電影中，多次出現了螺旋的形狀，比如唐志軍看到視頻錄像中兩道光是螺旋狀的；孫一通把看到的景象用泡泡糖捏成了雙螺旋；唐志軍在洞穴裏也看到了壁畫上的螺旋形狀；直到影片最後的特效，也做成了螺旋。

電影《宇宙探索編輯部》海報

影片的觀點認為，螺旋是“宇宙萬物運行的規律”，從宇宙中的星系到多種植物的中心，再到生命體的遺傳物質 DNA，都是螺旋的結構。

回到現實中，不少東西也是按照“螺旋”的法則生長和運作的。

01

植物中的螺旋

1. 羅馬花椰菜

羅馬花椰菜是由花椰菜和西蘭花雜交培育出的品種，它是分形學的代表。

它的花球表面由許多螺旋形的小花組成，整個羅馬花椰菜有將近 300 朵這樣的小花，每朵小花都是小型圓錐體，也是呈螺旋狀緊密排列的。

羅馬花椰菜，圖庫版權圖片，不授權轉載

小花以花球中心為對稱軸螺旋排列，這種圖案是斐波納契數列（又稱黃金分隔數列）的天然代表。

斐波納契數列的前兩項均為“1”，並且從第三項開始，每一項都等於前兩項之和，例如：1、1、2、3、5、8、13、21、34……

當項數足夠大時，前一項與後一項的比值越來越逼近黃金分割比例——0.618，人們在許多圖案設計上，都會考慮應用斐波納契數列。

2. 松塔

你可能經常在公園裏見到掉在地上的松塔，它是一種木質的、有鱗的“果子”。

仔細觀察，你一定會注意到它們的鱗片螺旋，鱗片可以在潮濕或寒冷時緊閉，保護它們的種子。然後在温度、濕度合適的時候打開，再讓風幫助種子傳播。

松果底部螺紋，圖片來源：Wikipedia

松果的底部螺旋圖案，從兩個方向細數這些螺紋構成的數字都是斐波那契數字。

如上圖的松塔，逆時針旋轉的線條數是 8，而順時針旋轉的線條數是 13；

除了 8 和 13，旋轉的線條數還有可能是 5 或 21，這些都是斐波那契數列中存在的數字；

而像 7、9、10、11、12 等不在斐波那契數列中的數字，則不會出現。是不是很神奇？

3. 多肉植物

在植物學中，分形被稱為**“螺旋葉序”**，即植物上的葉子呈螺旋排列。

許多多肉植物的葉子就是這樣緊密地按照螺旋結構捲曲生長，形成具有黃金分割比例的自相似螺旋——黃金螺旋。

這種排列方式有助於將雨水輸送到植物的核心，而且可以防止頂部葉子遮住底部葉子。

蘆薈的螺旋葉序，圖庫版權圖片，不授權轉載

當然也有一些不同的觀點。

曾有一位數學家提出假設，他認為所有植物，以及我們指紋的螺旋圖案的出現都是為了緩解生長所受的應力作用。例如，在植物中，隨着細胞在不同方向上的分裂生長，它們可能會因為受到相鄰細胞或組織的約束而經歷機械應力，這種應力會導致組織彎曲和摺疊。

02

什麼是“分形”

上面提到了那麼多次“分形”，分形就是螺旋生長嗎？

分形是幾何學中的一個概念，指的是簡單的相似圖案在不同維度上不斷重複，構成複雜的圖形或形狀，這種構形在自然界中無處不在。

早在 1967 年美國數學家本華·曼德博（Benoit B. Mandelbrot）在《科學》雜誌上上發表的一篇題為《英國的海岸線有多長？》的論文。文中指出，像是海岸線這種不規則圖形，如果選取的測量尺度不一樣，測量結果將相差甚遠。

如下圖，當選擇測量尺度很大時，細小的地方沒有測量，得到的值會比較小。

而用小尺度測量，得到的結果會大得多。用的尺度越小，得到的值將越大。

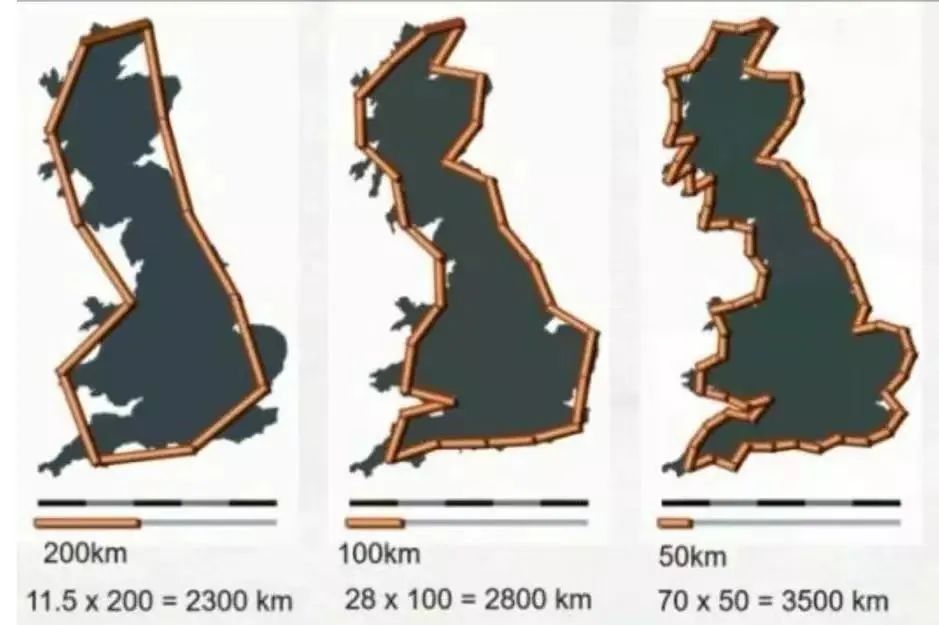
不同測量尺測量英國海岸線，圖片來源：Wikipedia

也就是説現實中這種複雜的不規則邊界的圖形沒有準確的周長，並且會隨着測量尺度的減小它的周長將趨於無窮。這便是分形理論的萌芽。

後來人們認為，如果這種不規則邊界呈現出一種小尺度和大尺度相似的特徵，並且無限細分下去都存在這種自相似性，那麼這種幾何形狀就可以被稱為“分形”。

03

分形並不都是“螺旋的”

其實，在日常生活中有很多分形的例子，除了開篇提到的羅馬花椰菜和松塔，像菠蘿的生長、冰晶的形成，也遵循分形規律。

1. 雪花

沒有兩片雪花是完全相同的，但是它們都有自己的獨特的分形。

圖庫版權圖片，不授權轉載

雪花的分支會產生自己的側分支，如果雪花不停的積聚水分並融合，那麼雪花可能會永遠這樣繼續下去。

我們生活中見到的雪花實際上就是經過無數次迭代形成的。

科赫雪花示意圖，圖片來源：Wikipedia

這其中最著名的分形圖案被稱為科赫雪花，它源於一個等邊三角形疊加另一個等邊三角形，然後再接二連三形成下一個等邊三角形。

科赫雪花經過無數次迭代後，它的邊角變得非常崎嶇，這會使有限面積的雪花藴藏着無限的周長。

這也與“海岸線有多長”的問題異曲同工。

2. 樹枝

對於植物來説，以分形的規律生長，可以讓它們最大限度地暴露在陽光下，進行良好的光合作用。同時，也能夠高效地將養分輸送到自身的各個部位。

樹木的生長是自然界中最典型的分形之一。

隨着樹幹的生長，樹枝從樹幹上長出來，而這些樹枝本身又會像樹幹一樣，發展出自己的枝條。

仔細觀察，你會發現整棵樹可以看作“Y”形的重複。

樹木分形，圖片來源：Robert Fathauer

這種分形設計，就像多肉植物的螺旋形，幫助樹木優化它們對陽光的照射，並防止頂部樹枝遮擋較低的樹枝。

3. 銅晶體

分形幾何在化學中也很常見，銅晶體正是一個典型的代表。

銅晶體像樹枝一樣向四面八方分支，每根分支又是一個新的生長點往下延續。

銅晶體，圖片拍攝：老貓

正是這樣的不斷分枝，形成固體金屬銅。

由於這種迷幻的樹狀結構和獨特的紅棕色，生活中銅晶體經常被當作藝術品。

4. 河流

當我們看地圖時，會發現河流總是呈蜿蜒的“S”形，雖然溪流有時可以形成一條直線，但隨着它們遇到不同障礙物干擾，很快就會變得彎曲。

只需一次擾動就可以擾亂河流的流動路線，使其全線彎曲。

圖庫版權圖片，不授權轉載

深入研究這些河流後會發現，它們的寬度是非常公式化，一般曲線長度總是通道寬度的六倍。

這種自相似性正是分形的特徵，也是世界各地河流看起來相似的原因。

5. 泡沫

在自然界中，當海浪衝擊或雨滴落下時出現的氣泡會產生一種自相似的模式，液體薄膜將各種大小的氣腔隔開。

大氣泡旁邊散佈着小氣泡，小氣泡旁散佈着更小的氣泡。

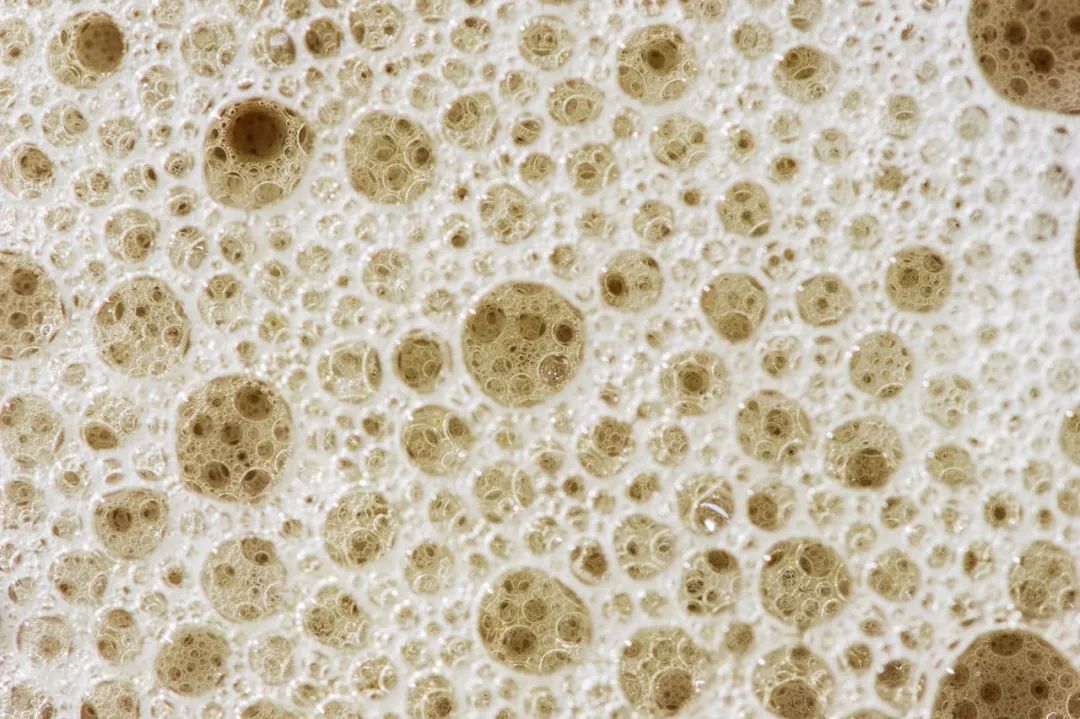
圖庫版權圖片，不授權轉載

我們在咖啡上、洗碗槽、浴缸中見到的泡沫都是一種分形的現象。

自然界中每一中的分形都有它自己的道理，你在自然界中還見到過哪些分形的現象？

參考文獻：

[1] “UA Mathematicians Predict Patterns in Fingerprints, Cacti.” University of Arizona. 2004.

[2] Peng, Sheng-Lung, Rong-Xia Hao, and Souvik Pal. “Proceedings of First International Conference on Mathematical Modeling and Computational Science.” Springer Nature. 2021.

作者：Denovo 科普作者

審核：張磊 北京大學北京國際數學研究中心 研究員