時間為何不同於其他維度?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!05-10 09:25

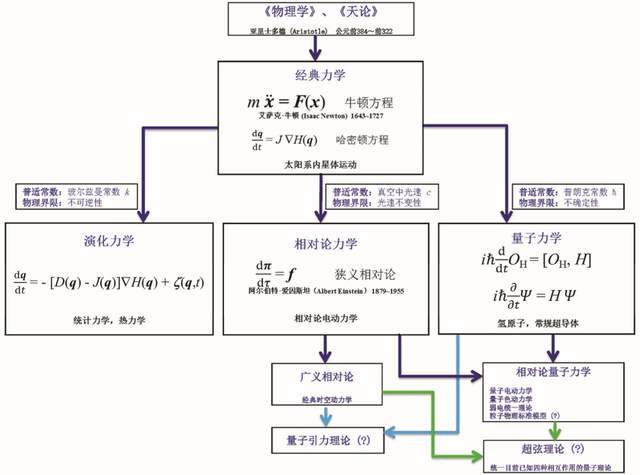
似乎所有人都知道時間的特殊性,但物理學——迄今最精密、最成功的科學怎麼處理它?梳理2000多年來物理學的基本運動理論的發展,一個初步的脈絡呈現在我們面前。亞里士多德認為時間維度與空間維度是互不影響的,空間維度可能更為重要——天上和地面的運動規律是不一樣的。牛頓引入絕對時間與絕對空間的概念,在經典力學中時間維度是與空間維度地位平等的。牛頓提出三大運動定律以後,物理學的基本運動理論一分為三:愛因斯坦的(狹義)相對論力學、量子力學和演化力學。三個力學理論分別引入一個普適物理常數:真空中光速c、普朗克常數h和玻爾茲曼常數k,各自界定了對物理世界認識的一個極限:光速不變性、不確定性和不可逆性。對時間的認識也一分為三:量子力學基本沿用經典力學的時間概念;基於相對論力學時間與空間統一了,可以在一定程度相互轉換,但基本的時序是相對性不變的,時間與空間有所不同;基於熱力學第二定律和耗散-漲落定理所代表的不可逆性,演化力學給予了時間一個特別地位。這些顯然還不是最後答案。三種普適力學若是統一,以後時間的作用怎樣?
撰文 | 敖平(上海大學物理系、定量生命科學國際研究中心,上海交通大學系統生物醫學研究院,現為四川大學教授)
從人類文明的曙光開始幾乎所有人都知道、或覺得知道時間是什麼,都感覺到時間在不停地流逝,過去、現在和未來是不同的。從古至今一直有人幻想能回到過去或知道未來,如各種穿越劇所演示。還有不少人想方設法讓時間流動變緩、甚至停滯下來,眾所周知的埃及法老企圖用木乃伊來實現永生、秦始皇尋求長生不老之術就是這種不太成功的努力。人類對自然知識的積累到一定水平後開始理性地解釋世界,試圖瞭解時間這一現象的本質是什麼和如何被描述,產生了各式各樣系統的理論猜測和玄思。有起源於近東的宇宙有始有終的線性型體系;有印度的週期、輪迴;也有我國《易經》裏的不停變化。現存系統、努力去接近經驗觀察的體系由希臘亞里士多德提出並總結在他的《物理學》和《天論》兩部著作中(圖1)。這個古希臘知識體系強調邏輯的一致性,追求現象背後的動因和本質,明確認定時間的獨立地位,同時也認為天空上星體的運動與地面附近物體的運動是截然不同的。這是物理學中的運動規律明確表達的開始,垂範學術界近2000年[1]。
01
牛頓的絕對時間
經過2000年左右的探索,人類逐漸認識到亞里士多德體系的不足,首先有對時間概念上的持續困惑。如對亞里士多德研究很深的著名宗教學者聖·奧古斯汀(St Augustine)很早就説道,“什麼是時間?如果沒人問我,我很清楚;如果有人希望我解釋,我則不清楚”。亞里士多德運動規律與實驗的偏差也積累到一個不可調和的程度,傳説中的伽利略(Galileo)比薩斜塔實驗非常有效和形象地説明當時的流行理論與實驗的不符合。在總結前人的研究成果和他自己的實驗、理論研究的基礎上,牛頓在1687年系統地提出了著名的三大運動定律:
第一定律:每個物體如果沒有外界影響使其改變狀態,那麼該物體仍保持其原來靜止的或等速直線運動的狀態;
第二定律:動量的變化與所施加的力成正比,並沿力的作用方向發生;
第三定律:對於每一個作用力,總存在一個與之相等的反作用力和它對抗。
三大定律與牛頓發現的萬有引力定律一起實現了對天空中星體和地面上物體運動認識的統一[2],也讓人類第一次有了對自然規律的定量、精密的描述,成為經典力學的基礎。
為了更好地描述運動,牛頓發明了微積分(我懷疑可能是好的工具幫助他發現了新的運動規律)。不過由於這個數學方法太新,牛頓在他的書中仍然用古老但傳統的數學方式——幾何來表述三大運動定律,這導致我們現在閲讀這部鉅著的困難。我們現在常用的牛頓方程表述F=ma是牛頓提出三大運動定律50年後由伯努利(Bernoulli D)給出(圖1),加速度a由牛頓記號表示,

牛頓第一定律界定了慣性參考系的存在,由於伽利略相對不變性的保證,時間的變化在所有慣性系中是一樣的——時間的絕對性。慣性系需要的空間是歐幾里德(Euclid)空間,甚至經過嚴謹、具有批判精神的哲學家之一康德(Kant)的分析,仍認為是先驗地存在的。時間和空間在經典力學中是相互分離的,是兩個不同的物理量或維度,但作為座標具有一種平等的地位。
應用萬有引力定律牛頓初步解決潮汐(月球和太陽的引力所導致)這一2000年難題,伯努利在1740年進一步發展平衡潮理論,結合牛頓方程,拉普拉斯(Laplace)在1776年提出動力潮理論,完整地解釋了潮汐;哈雷(Halley)預測了一個慧星的運動週期——哈雷彗星在1758年如期歸來;科學家們預測了新的行星的存在,海王星在1846年被觀察到。經典力學取得了巨大的、前所未有的成功,它成為了科學理論的一個範本,影響遠逾物理學的範圍。
經典力學清楚地表明定量描述一個物理現象需要3個基本要素:運動方程——牛頓方程;物體本構方程——確定質量和力;初始和邊界條件。運動方程和初始條件與時間關聯,而力或相互作用的陳述和邊界條件需要空間。物體在時空中的行為是可確定的。經典力學的成功給我們提供了一個普適物理理論的例子:能描述非常廣泛的實驗和經驗事實、沒有確定已知的實驗反例、沒有可預見的應用邊界。經典力學有很多數學上等價表述形式,與我們論述相關的是著名的哈密頓(Hamilton)方程。它是關於物體在相空間q中的運動方程,

相對論力學中的時間
第一個成功的突破口就是在絕對時間和空間這對概念。愛因斯坦長時間地思考了麥克斯韋(Maxwell)方程中伽利略相對不變性的不成立這個理論不一致問題,認為應該修改經典力學的相對性概念——揚棄伽利略相對不變性中時空的絕對性。1905年,愛因斯坦[4]提出了兩條簡潔的原理,相對性原理和光速不變原理:
(1)凡是對力學方程適用的一切慣性座標系,對於電動力學和光學的定律也一樣適用;
(2)光在真空中的速度c同發射體的運動狀態無關.
這兩條原理構成狹義相對論的理論基礎,帶來一系列觀念的革命性變化。變化之一是同時性的可操作性建立,在不同的慣性系中不再有同一的同時性,時間的流逝在不同的慣性系中會是不一樣的,狹義相對論和經典力學的時間同時性的不同,被著名的雙生子佯謬形象地揭示。另一個直接的推論是時間維度、空間維度不再是相互獨立,它們可以相互轉化,一起構成四維時空,經典力學的絕對時空理論上不再成立。
重新定義相對性不變的四維力f和四維動量π,用固有時間或原時τ表示時間,力學運動方程仍具有同樣簡潔、優美的形式(圖1),能與麥克斯韋方程完美地一致結合。相對論力學還預測能量和質量不再相互獨立,可以相互轉化——愛因斯坦著名的質能關係E=mc2。當然,在低速極限下,相對論力學回歸經典力學。
100多年過去了,(狹義)相對論力學通過了迄今為止能做的、針對它的實驗的檢驗,它的應用也給我們日常生活帶來巨大影響。它已替代牛頓方程成為一個普適運動方程,是現代物理學的基礎之一。1915年,愛因斯坦再次推廣相對性原理為廣義相對性原理,把萬有引力也納入相對論力學的框架中,進一步發展對時空的理論,再次增進了我們對時空的理解。他用黎曼(Riemann)幾何替代歐幾里德幾何,用彎曲的時空替代平直的時空。我們所處的時空不單不是絕對或先驗的,還依賴於其中的物質運動,時空可能會有起點。
從認識論的角度,黎曼空間的存在和應用也提示我們歐幾里德空間不是哲學意義下先驗的,廣義相對論再次促成了對整個時間、空間觀念的變革。從物理學本身發展的角度,相對論力學這個發展的例子告訴我們一個成功的新物理理論需要具備3個基本條件:包括舊理論的適用範圍;預測新實驗並通過其檢驗;有孕育新思想、新概念的能力。另一個眾所周知的例子是經典力學:作為穩態極限,它成功地吸收了靜力學如著名的阿基米德(Archimedes)浮力定律並具備上面討論過的其他兩個基本條件。
儘管相對論力學把時間、空間結合在一起,四維時空給我們時間維度、空間維度等價的想象,但它們之間的變換不像空間維度之間的變換那樣任意。類時、類空和類光的四維時空是相對性不變的,我們不能把類時變換為類空。四維時空中發生的事件仍然有一個基本時序。時間維度與空間維度仍然不一樣。
03
量子力學中的時間
第二個成功的突破口的成果是量子力學[5]。量子力學基本上還是沿用經典力學的時間概念,但從一個完全不同的角度變革了我們關於空間的概念:描述物體運動的相空間是有結構的。簡單的例子是相空間中的位置x和動量p滿足一個對易關係,[x, p]=ih,不再相互獨立,它們的乘積不能交換,xp≠px。這個對易關係也是一對共軛物理量之間不確定性關係的典型例子。從1900年普朗克(Planck)發現普適常數到1925年海森堡(Heisenberg)發現第一個量子力學的表述花了至少兩代物理學家四分之一世紀的時間。海森堡方程用算符OH表示物理量,直接用了對易關係(圖1)。1926年建立的薛定諤(Schrödinger)方程也是常用的表述,用波函數ψ描述物體的時空狀態,把相空間結構和對易關係隱含在其中。這兩種描述繪景都需要首先確定系統的哈密頓量。在普朗克常數很小的條件下,量子力學回歸到經典力學。
量子力學立即在從玻爾(Bohr)開始氫原子的理論研究中取得成功。一個非常成功的應用例子是超導現象:在我們熟知的一些科學家如費曼(Feynman)、朗道(Landau)等沒有取得成功的情況下,一個由教授、博士後、研究生組成的理想的研究團隊——但直到今天在專家範圍外仍然不知名的團隊在1957年發現了巴丁-庫珀-施裏弗(Bardeen-Cooper-Schrieffer)常規超導理論(巴丁是迄今為止唯一得過兩次諾貝爾物理學獎的科學家)。這是一個非常深刻的理論,影響到物理學很多領域的發展,包括基本粒子物理的希格斯(Higgs)機制。與相對論力學一樣,量子力學是現代物理學的基礎之一,也對我們的日常生活有巨大影響,這是替代經典力學的第二個普適理論。
量子力學對時間、空間還各有一點重要突破。除了指明相空間有結構之外,量子力學明確表明描述物體運動的相空間不限於我們常見的三維空間(相空間是六維),別的維度也一定存在,別的空間方式也可用——恰當的一般空間是希爾伯特空間,完全脱離經典力學的相空間。例如基本粒子如電子的自旋,必須作為獨立的、額外的自由度接受下來,這對後續量子場論的發展影響巨大。在時間上,量子力學表明一定程度的逆時間運動是可能的,從它的路徑積分表述來看尤其明顯:逆時間路徑沒有被排除,它的物理後果迄今還沒有被探索清楚。量子力學與相對論力學相結合的狄拉克(Dirac)方程獲得瞬時的成功。經過各自多年的幾番努力,電磁相互作用、強相互作用、弱電相互作用的相對論量子場論化也獲得成功。粒子物理的標準模型,統一電磁、弱和強相互作用的理論,也獲得一定成功。這些成功理論的數學結構都屬於楊振寧、米爾斯(Mills)所發現的規範場。但是,萬有引力或廣義相對論的量子化,還沒有成功,有很強的理論矛盾;從量子場論的角度來包括廣義相對論,如超弦理論,也還沒有成功,還沒有一個新的實驗驗證,它們在圖1中用問號標識。在一定意義下我們又回到1905年之前的狀態:各個理論之間還不完全融洽。這表明存在很深刻的理論問題,關鍵很可能是時間與空間在相對論中和在別的一般物理理論如量子力學中到底有何差別,有待我們繼續探索。
04
演化力學中的時間
儘管它們的物理內容和數學結構完全不一樣,量子力學與相對論力學的運動方程都有一個從經典力學帶過來的共同性質:對於時間反演動力學是可逆的,孤立系統的能量是守恆的,信息或熵也是守恆的。有時人們會被自己手中的問題誤導,會忘掉這個重要性質,譬如霍金(Hawking)就曾經忽視它而輸了關於黑洞的宇宙信息守恆的賭,現在他認為黑洞是會帶量子“軟毛”的,會保留信息[6]。但是,過度強調這個守恆性質可能會導致另一個極端,把時間從物理規律的表述中取消,沒有時間這個維度,從而把時間的存在看成是一種幻象[7]。這也是可以理解的:如果把能量看成“天”,把信息或熵看成“道”,我們已知兩種普適動力學對於孤立系統無非是説“天不變、道也不變”。我們好奇的是,經典力學以後是否還有別的、不守恆的、第3種普適力學結構的可能?
事實上,19世紀中葉出現的熱力學首先對這個問題提供了肯定回答的可能。早於相對論力學和量子力學的發展,熱力學第二定律[8]明確陳述一般動力學過程是不可逆的,它是人類發現的普適規律之一,迄今沒有任何實驗、經驗上的例外。但是,熱力學不是真正的動力學,這讓它催生了兩個重要問題:它的存在與已知的普適運動規律相容嗎?如果相應新的運動方程存在的話,一般形式會是什麼?
從麥克斯韋、玻爾茲曼(Boltzmann)、吉布斯(Gibbs)等開始的150多年研究對第一個問題給出了肯定回答:相容;併產生了一門對應的、應用範圍與熱力學一樣廣泛和成功的學科——統計力學[9],是現代物理學的一塊重要基石。對第二個問題的回答有兩個相反的努力方向:不可逆性仍然由可逆的運動規律中產生;或尋找全新的結構。從玻爾茲曼開始的物理學主流希望不可逆性能夠從已知的運動規律產生:經典力學和量子力學。很遺憾,這種努力經過150多年還沒有成功:常見的問題是明確地或隱蔽地總是把不可逆性的假設引入到論證過程中。其餘的研究要麼論證過程有錯、要麼系統太特殊。但這個探索帶來了很多重要成果,加深了我們對運動規律的理解,例如混沌的發現與研究[10]。
第二個方向把研究者們帶到全新的領域,遇到的不可逆的運動方程太多了,可用的方法真是“八仙過海,各顯神通”,一般的意見對能否得到肯定的答案一直是不確定的。譬如直到近(甚至現在)很多人對一般非平衡過程中是否存在類似的能量函數H、統計力學是否存在一個普適的力學框架仍然持一個懷疑態度[11]。幸運的是,第一個對應於統計力學或熱力學的一般運動方程終於出現了,它的形式也非常“簡單”(圖1)。

隨機“力”ζ與擴散矩陣D的關係是統計物理中著名的耗散-漲落關係的一個特例,但在演化力學的表述中是作為定義出現的,可稱為“F定理”,這意味着它在演化力學中普遍成立,實驗上是可以檢驗的。這個定義可以看成牛頓第三定律的一個推廣:物理體系如何與未知的世界相互作用。更進一步的研究發現系統的擴散矩陣和摩擦矩陣還應該滿足一個普適的關係[12],愛因斯坦關係——摩擦係數與擴散係數乘積是常數——在高維、非線性、無細緻平衡情況下的推廣,是一個新的預測,也能被實驗檢驗。
演化力學預測了一系列隨機動力學等式,其中一部分是熟知的熱力學不等式的推廣,可由實驗檢驗[12]。它也指出目前基於平均場意義下的熱力學第二定律會在漲落大的情況下出現與實驗的偏差,應該重新檢驗其陳述。演化方程所依賴的新的隨機積分[14]在物理系統中也是可以檢驗的,意義類似於廣義相對論中空間是否彎曲。成功的新物理理論所需要具備的3個基本條件演化力學都能滿足。數學上,演化力學是基於新發現的一個強有力的數學結構[16, 19]:一個隨機過程中總存在一個類似於物理中能量的函數,記為H,動力學過程可以分解為兩部分:保持H不變的部分,記為J讓H減少的部分,記為D,由隨機項的方差確定。演化力學可以作為第3個普適力學,是現代物理學的另一基礎。
演化力學提供了描述非平衡態過程的一般框架,它的穩態極限——統計力學是目前應用廣範、成功的物理理論[20]。不但成功地運用在宏觀世界,而且也成功地運用在量子場論描述的微觀世界和廣義相對論表述的宇觀世界。演化力學以一種完全不同於量子力學的方式引入不確定性,假設物理體系是開放的、實際過程總是不可逆的。在量子力學中不確定性是關於相空間或共軛物理量的,而運動過程是可逆的。演化力學中的可逆性類似於科學的重要基石之一——測量,測量過程是不可逆的。在經典力學中測量對系統的影響在理論上可以無限地小以至於能被忽略不計,而在量子力學中測量有小單位,~h In2,普朗克常數和比特。從這個角度演化力學會對解決量子力學中的測量問題——玻爾和愛因斯坦終生討論但沒有獲得共識的問題提供一個重新考慮的思路。
與量子力學一樣,演化力學基本沿用經典力學的時間概念,在慣性系之間不做區別,對空間的要求也與量子力學一樣,可以是任意空間。這讓它甚至能應用到物理學的範圍以外,事實上它的發現就受到生物學中達爾文(Darwin)演化過程的啓發[12]——玻爾茲曼就曾經這樣猜測過,但他卡在怎樣處理無細緻平衡的運動。它與量子力學和相對論力學(包括經典力學)大的不同是:在演化力學中能量和信息都不守恆了,把不可逆性顯式地容納在內,明確揭示時間維度和空間維度的不一樣。
05
展望
從運動規律的發展歷程中我們看到時間維度是如何與其他維度不一樣的。目前我們所知的3種普適力學各有一個普適常數:c,h和k,分別揭示了物理世界的一個認識界限:光速不變性、不確定性和不可逆性(圖1)。其中,兩個界限與時間相關,在一定程度上物理學已回答了時間為何不同於其他維度。更完整的回答可能涉及對一個客觀世界的根本規則——因果關係的更深刻理解,也許要等到對3種普適力學有更進一步理解之後。
此外還有一系列的與時間相關的問題需要回答,難度也許要小一點:我們注意到相對論量子場論是相對論力學與量子力學的優美結合,但它連接到演化力學或統計力學就顯得特設性很強,目前好的做法之一是久保-馬丁-施温格(Kubo-Martin-Schwinger)條件,在理論上還可以比這個條件做得更好嗎?超弦理論中的多宇宙理論已經在應用演化理論,後者的角色可以更大嗎?我們能把3種普適力學都統一在一個理論構架中嗎?這個統一是會在統一四種相互作用之前還是之後?我們的宇宙到底是孤立的還是開放的?等等。對有志探索的人們,也許第一步是瞭解物理學已經取得的、比較確定的成就[21]。然後,體驗、享受你的探索歷程。或者,純粹來欣賞人類理解時間這一艱苦卓絕的奮鬥。
參考文獻
[1] Aristotle. Complete Works of Aristotle (v1). New York: Princeton University Press, 1984
[2] Newton I. The Principia: Mathematical Principles of Natural Philosophy. New York: University of California Press, 1999 [Newton I. 趙振江, 譯. 自然哲學的數學原理. 北京: 商務印書館, 2006]
[3] Peng H W, Xu X S. Introduction to Theoretical Physics (in Chinese). Beijing: Peking University Press, 1998 [彭桓武, 徐錫申. 理論物理基礎. 北京: 北京大學出版社, 1998]
[4] Zhang Y Z. Experimental Foundation of Special Relativity (in Chinese). Beijing: Science Press, 1979 [張元仲. 狹義相對論實驗基礎. 北京: 科學出版社, 1979]
[5] Wang Z X. Principle of Quantum Mechanics (in Chinese). 2nd ed.. Beijing: Peking University Press, 2008 [王正行. 量子力學原理. 第 2 版. 北京: 北京大學出版社, 2008]
[6] Hawking J W, Perry M J, Strominger A. Black holes have soft quantum hair. Phys Rev Lett, 2016, 116: 231301
[7] Barbour J. The End of Time. New York: Oxford University Press, 2000
[8] Wang Z X. Thermodynamics (in Chinese). 2nd ed. Beijing: Peking University Press, 2014 [王竹溪. 熱力學. 第 2 版. 北京: 北京大學出版社, 2014]
[9] Gibbs J W. Elementary Principles in Statistical Mechanics. New York: Charles Scribner’s Sons, 1902 [Gibbs J W. 毛俊雯, 譯. 統計力學的基本原理. 合肥: 中國科學技術大學出版社, 2016]
[10] Hao B L. Directions in Chaos (1&2). Singapore: World Scientific, 1987, 1988
[11] Lu X Y, Lin J Z. Can we develop a general theory of the dynamics of turbulent flows and the motion of granular materials (in Chinese)? Chin Sci Bull, 2017, 62: 1115–1118 [陸夕雲, 林建忠. 能否發展關於湍流動力學和顆粒材料運動學的綜合理論? 科學通報, 2017, 62: 1115–1118]
[12] Ao P. Emerging of stochastic dynamical equalities and steady state thermodynamics from Darwinian dynamics. Commun Theor Phys, 2008, 49: 1073–1090
[13] Ao P. From N=∞ to N=1: Arrival of dynamical foundation for statistical mechanics (in Chinese). In: TD Lee Library, ed. Essays in Honor of the 90th Birthday of TD Lee. Shanghai: Shanghai Jiao Tong University Press, 2016. 281–287 [敖平. 從 N=∞到 N=1: 期望已久的統計力學普適動力學基礎已到來. 李政道圖書館, 編. 心通天宇——李政道教授九十華誕文集. 上海: 上海交通大學出版社, 2016. 281–287]
[14] Ao P, Kwon C, Qian H. On the existence of potential landscape in the evolution of complex systems. Complexity, 2007, 12: 19–27
[15] Qian H, Ao P, Tu Y, et al. A framework towards understanding mesoscopic phenomena: Emergent unpredictability, symmetry breaking and dynamics across scales. Chem Phys Lett, 2016, 665: 153–161
[16] Ao P. Potential in stochastic differential equations: Novel construction. J Phys A, 2004, 37: L25–L30
[17] Kwon C, Ao P, Thouless D J. Structure of stochastic dynamics near fixed points. Proc Natl Acad Sci USA, 2005, 102: 13029–13033
[18] Ma Y A, Tan Q J, Yuan R S, et al. Potential function in a continuous dissipative chaotic system: Decomposition scheme and role of strange attractor. Int J Bifurc Chaos, 2014, 24: 1450015
[19] Yuan R, Tang Y, Ao P. SDE decomposition and A-type stochastic interpretation in nonequilibrium processes. Front Phys, 2017, 12: 120201
[20] Ao P. The work of David J Thouless: The discovery of topological phase transition led by curiosity (in Chinese). Chin Sci Bull, 2017, 62: 1199–1203 [敖平. 大衞 邵勒斯的治學和建樹: 純粹探索凌絕頂. 科學通報, 2017, 62: 1199–1203]
[21] Brown L M, Pais A, Pippard B. Twentieth Century Physics (I-III). New York: CRC Press, 1995 [Brown L M, Pais A, Pippard B. 劉寄星, 譯. 二十世紀物理學(1–3). 北京: 科學出版社, 2014]
本文原文發表於《科學通報》2018年第2期,經作者授權發表於《返樸》。
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。