安德森四原則:從對稱性破缺到複雜性湧現_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!06-22 09:30

撰文 | David C. Krakauer
翻譯 | 劉志航
審校 | 劉培源
編輯 | 梁金
論文題目:
Symmetry–simplicity, broken symmetry–complexity
論文鏈接:
https://royalsocietypublishing.org/doi/10.1098/rsfs.2022.0075
「 摘要 」
複雜現象的湧現在兩種情況下有可能出現:一是當基本的物理對稱性被打破時;二是當選擇特定的基態(ground states)來執行機械工作和存儲適應性信息時。在幾十年的研究進程中,菲利普·安德森(Philip Anderson)從複雜系統的對稱性破缺(broken symmetry)中列舉了幾個關鍵原則。這些原則包括湧現性、阻挫隨機函數(frustrated random functions)、自主性和廣義剛性(generalized rigidity)。安德森四原則是演化功能湧現的先決條件。David Krakauer 撰文總結了這些觀點,並簡要討論了近期與功能對稱性破缺相關概念的擴展,包括信息、計算和因果關係。
「 超越對稱性 」
“在此之前的討論是關於裝飾和晶體中存在的幾何對稱性,是時候結束討論了。這最後一次講座的主要目標是展示在基本的物理和數學問題中對稱性原則的作用,並從這些和其之前的應用中提出對原則本身的最終普遍陳述。”
——Symmetry. Herman Weyl.
“於是我開始尋找日常世界的’Aufbauprinzips(結構原則)’。我很欽佩 Frohlich 的關於電介質理論的書,因為它採取了同樣的觀點;我在早期的鐵電體工作中遇到了它。更為重要的是,我開始認識到對稱性破缺概念的重要性,這一直是我生活中的長期興趣。對稱性破缺是“多者異也”(more is different)背後的湧現過程的最明顯實例。”
——A Career in Theoretical Physics. Philip Anderson.
在赫爾曼·外爾(Herman Weyl)1952年的專著《對稱》(Symmetry)[1]中,他基於應用於物理領域的數學,總結了一種強有力的現實視角。外爾提出,物理科學最終是一種以對稱性分析為基礎的探究形式。在物理學中,大量與對稱性相關的概念,包括時空對稱性、諾特定理、規範對稱性和超對稱性,這些概念將不變性及其衍生物——普適法則(universal laws),置於對非生命世界的研究核心。這一努力的成功是毋庸置疑的,因為對稱性在描述保守動力系統的結構和物質平衡態方面具有重要意義,涵蓋了從最大尺度的天體力學,到分子尺度的晶體學點羣,再到量子尺度上的酉羣(unitary group)。對稱性原理(物理定律在各種變換條件下的不變性)及其通過基本對稱運動定律的體現,為追求宏大的萬物理論提供了基礎(在該理論中,宇宙模型是自下而上地組裝)。

菲利普·安德森(Philip Anderson)的研究源自凝聚態物理,而非粒子及其相互作用。他畢生致力於更廣泛的自上而下的流程或構建原則。通過這些原則,微觀相互作用最終被其宏觀產物所涵蓋。1977年,安德森獲得諾貝爾物理學獎,以表彰他在磁性和無序體系電子結構的基礎理論研究的貢獻。安德森關於宇宙宏觀結構發展的研究在1972年達到頂峯,他發表了反還原論的物理學湧現宣言,即《多者異也》(More is Different) [2]。在通向“多者異也”的二十年時間裏,一直到1980年代和1990年代,安德森試圖將複雜現象建立在統計物理學的宏觀定律之上。他認知工程(epistemic project)的一部分是促成聖塔菲研究所在1984年成立,他也在論文《通往複雜性理論的八重途徑:序章》(The eightfold way to the theory of complexity: a prologue)中總結了自己的動機。這篇文章首次發於1994年[3],標題是對蓋爾曼的強子結構八重道分類(Eightfold Way)的致敬。安德森的興趣在於解釋那些不能從物理學基本對稱定律中預測的相同結構。他所有工作的基礎概念,也可以説是所有複雜現象的基礎概念,就是對稱性破缺。
對稱性破缺的後果多種多樣,但對於複雜性研究最有意義的是我稱之為安德森四原則,它們包括:(i) 通過多樣性或縮放引起的湧現性質,(ii) 阻挫隨機函數的重要性,(iii) 自主性的要求,以及 (iv) 廣義剛性的屬性。總的來説,安德森四原則主要是針對平衡宏觀態而得出的,它們為我們理解在非平衡狀態下通過耗散性或驅動性動力學引發的準平衡結構的湧現提供了必要的基礎。這些原則在描述適應性功能方面還存在不足,因為適應性功能超越了任何僅限於平衡結構的理論範疇,但它們應該成為任何此類理論的組成部分。
在接下來的部分,我將對這些想法進行總結,並在可能的情況下擴展它們,包括近期發現的結果和現象,以更直接地涉及適應性結構和功能的考慮。
對稱性破缺:創造超越物理學的空間
安德森在《多者異也》開頭引入了對稱性破缺的概念,描述了對稱物理定律在解釋常見的大分子結構時的尺度依賴限制。他選擇的例子是氨分子的金字塔結構。氨分子(NH3)被認為具有金字塔狀的結構,以每秒大約300億次的頻率在兩種狀態之間反轉或量子隧穿(氨分子涉及的對稱性是宇稱parity,即空間反演對稱)。這個過程的結果是,氨的靜態分佈是兩個相互可逆的金字塔的混合物。氨的兩個構型之間的隧穿勢壘很低,意味着“一個系統的態,如果是定態的話,其對稱性必然與支配它的定律相同”。然而,當考慮稍大一點的分子如磷化氫(PH3)時,反轉速率至少慢一個數量級,而三氟化磷(PF3)則更大,反轉速率至少再慢一個數量級。當尺度達到生物活性分子,甚至是最簡單的碳水化合物的尺度時,宇稱對稱性的整體概念就崩潰了。分子的靜態分佈主要由初始條件而不是運動定律所主導。為了解釋觀察到的結構分佈,我們需要一個超越基本定律簡約性的解釋。超越基本定律描述的附加參數化有效地“計算”了對稱性破缺,並通過適當的模型複雜性度量提供了湧現的證據。
在最近的一篇綜述中,Buhse 等人[4]將這個觀點擴展到非平衡狀態下的手性分子,並討論了與手性對稱性破缺相關的幾種有偏不完美分岔的基本機制。在這種情況下,化學對映體(化學鏡像)的混合物被環境手性過程推向穩定的同手性溶液,其中包括流體渦旋和偏振光。
在1994年的文章《關於對稱性破缺的一些一般性思考》(Some general thoughts about broken symmetry)中[5],安德森對這些主題進行了重要的擴展。在這篇文章中,引入了自主性和廣義剛性的概念,我將在後面的部分進行介紹。正如朗道(Landau)關於二級相變理論[6]所描述的那樣,在這裏,我想簡要提到安德森對相變和對稱性破缺的強調。眾所周知,朗道表明“從晶體向液體或不同對稱性的晶體的每個轉變,都伴隨着某些對稱性元素的消失或出現”。對於二級相變(按Ehrenfest的理解),“與物體對稱性變化相關的連續相變(就像液體和氣體之間的連續相變一樣)是絕對不可能的”。安德森將這樣的相變描述為朝向更低對稱性的運動。例如,凝聚態物質(如某些液晶)中,旋轉對稱性(各向同性)或平移對稱性(均勻性)的消失。對於安德森來説,通過相變改變的物質狀態的序參量應被視為對稱性破缺程度的度量,而在朗道理論中,這通常是有序性增加的程度。此外,序參量應源自對對稱運動定律的理解。通過這種方式,我們可以非常準確地看到基本定律和湧現結構之間的偏離程度。
我懷疑1994年的論文無意中造成了許多混淆的陳述,其中湧現和相變被視為同義詞。首先,正如安德森迅速指出的那樣,他的觀點並不適用於所有相變,比如最為人所知的液體到氣體的相變,該相變保持了對稱性。而對於轉變為凝聚態對稱性破缺(有序度增加)的相變,正是它們能夠支持更多破缺對稱(增加無序)的潛力使得它們對生命系統如此重要。正如他在《多者異也》中寫道:“儘管晶體是對稱的,但它的對稱性仍低於完全均勻性”,以及“這種‘載有信息的結晶性’似乎對生命至關重要。”後者當然是對於薛定諤在《生命是什麼?》(What is Life?)中關於遺傳的非週期晶體猜想的致敬[7]。
1. 湧現(性)
湧現的概念可以非常簡單地描述為在不損失解釋能力的情況下,成功地將物理學基本定理分解出來。安德森將破缺對稱作為實現這種效果的主要機制。氨基酸是同手性的,儘管它們的對映異構體出現的概率相等。同樣的情況也適用於整個細胞的手性,與原細胞的核酸、蛋白質和碳水化合物領域的自發鏡像對稱性破缺相關[8]。物理定律無法充分解釋這種變異。在更寬泛的組織層次上,這些定律對於肌肉收縮的動作電位編碼、Lisp 代碼中錯誤的影響、為什麼有些食物嚐起來很苦,或者是什麼讓 Wallace Stevens 的詩行得通等問題,都沒有解釋力。所有這些都是不同尋常地不受物質基本結構法則支配的現象的候選者。
在《多者異也》中,安德森提出了一個包含兩列的表格,X列和Y列。在X列中,他列出了遵循Y列科學定律的科學領域的列表。例如,X(化學)遵循Y(多體物理學),X(細胞生物學)遵循Y(分子生物學)。關鍵在於,“遵循”和“決定”( ‘obey’ and ‘determine’ )並不是同義詞。我們可以説,遵循和決定之間的區別是關於對稱性破缺數量的陳述。還原論的操作定義是對稱性在物理定律中的極限情況,它決定了實證可觀測量的分佈情況。在還原論下,遵循和決定的含義變得相同。在複雜性研究中,我們追求的是針對感興趣的量具有決定性解釋的有效理論,而這些理論與它們遵循的物理學相差甚遠。
在某個階段,對稱性對宏觀行為變得如此邊緣化,以至於甚至對稱性破缺的概念也失去了依據。因此,“在某個點上,我們必須停止談論對稱性的減少,開始稱之為複雜性的增加。所以隨着每個階段增加的複雜性,我們繼續沿着科學的層級結構向前發展”。這不僅僅是累積自由參數的問題,而是發展全新的概念結構。考夫曼(Kauffman)在基因控制迴路(或我們現在所稱的調控網絡)方面的工作是開創性的,他引入了對能夠產生穩定分化狀態的最小規則系統的關注。在複雜性領域中,湧現規則而不是基本定律體現了複雜性的特點[9]。
我發現 Laughlin 等人的工作[10]是對安德森思想的一個非常有説服力的延伸,特別是他們在《中間道路》(The middle way)中對介觀尺度組織的闡述。在超越對稱性破缺的基礎上,他們引入了“受保護狀態”(protected states)的概念,這些狀態對基本運動方程的微小擾動具有穩定性。因此,“超流性、鐵磁性、金屬導電性、流體力學等都是物質的‘受保護‘性質——無論細節如何,一個系統與另一個系統可靠地具有相同的一般行為”。以三氟化磷為例,防止隧穿的保護是通過化學勢和分子波函數的性質提供的。對於大分子,如DNA的保護是通過複雜而進化的誤差修正機制實現的,這些機制被強加在主要的信息傳遞結構上。生命尺度上的湧現最好是以保護或魯棒性[11]的機制來考慮,這些機制能夠對大幅度擾動進行屏蔽,從而使生物分子及其集合的“有效”運動方程得以調節。通過這些屏蔽機制,例如在疾病監測的情況下,我們就可以用包含四個字母表的大大簡化的字符串,以替代原本需要精確描述 RNA 和 DNA 所需的極其複雜的生物學框架。
2. 阻挫隨機函數
1983年,安德森撰寫了一篇相對被忽視的論文《關於生命起源前進化的建議模型:混沌的運用》(Suggested model for prebiotic evolution: the use of chaos)[12]。這篇論文對生命起源並沒有提供特別有啓示性的信息,但它包含了關於耗散結構理論所面臨的挑戰的幾個重要洞見,並強調了凍結漲落作為適應現象啓示的關鍵作用。
耗散結構理論是由普里高津(Prigogine)在1978年的一篇論文《時間、結構和漲落》(Time, structure and fluctuations)[13]中引入的,該論文總結了布魯塞爾大學過去十年在非平衡熱力學領域發展起來的有關生命的新理念。該理論的核心思想是,非平衡結構為生命系統中的原始秩序提供了重要的來源,例如在貝納德對流中產生的渦旋。普里高津認為,這些規律性現象在玻爾茲曼的平衡秩序原理(Boltzmann’s equilibrium order principle)中是一個盲點。在驅動系統中,相干態(耗散結構)可以自發地湧現,並通過與外界能量交換而穩定下來。這些結構的特點是它們對“表徵化學系統環境的全局特徵非常敏感,例如大小、形狀、對錶面施加的邊界條件”等等。對於安德森來説,這種敏感性被證明是一個不可逾越的障礙(我將在後面關於自主性和剛性的章節中討論),即在沒有一些機制使平衡結構從動力學中凝聚出來時,無法利用穩態對稱性破缺來可靠地儲存信息。
安德森將這個問題描述為在穩定性需求與多樣性要求之間的協調問題。然而,在一個驅動系統中,雖然可能會出現許多耗散結構,但大多數都是短暫存在的,觀察到的形式受到其不穩定性的嚴重限制。問題在於,儘管“可以很容易地建立一個具有穩定結果的過程,但這是以犧牲關鍵程度的多樣性為代價的”。由於穩定性將從大量候選結構中篩選出一個非常小的“可行”集合,因此“混沌是一個先決條件:我們需要一個生存概率,它是分子組成的一個固定但混亂的函數”。安德森認為,從平衡統計力學角度來看,將穩定性與持續的隨機源相結合的最有説服力的候選系統是自旋玻璃。這是一個具有自旋哈密頓量的系統,
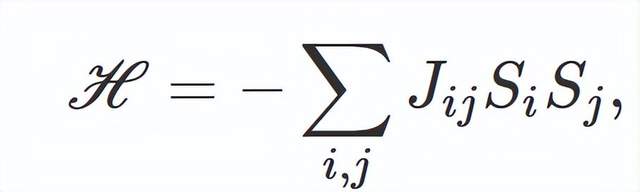
安德森利用自旋玻璃的阻挫隨機函數,定義了一個簡單的序列生長、分裂和互補鹼基配對模型。在一個相對較弱的隨機場的存在下(即對系統自旋狀態施加的環境偏置),這個模型能夠支持一個多樣化的穩定序列集合。自旋玻璃在適應性現象中的另一個更有説服力的應用是由 Hopfield 提出的內容尋址記憶[14]。Hopfield 的重要觀察結果顯示,由受阻挫隨機相互作用提供的簡併基態能夠存儲位序列。因此,系統內在的對稱性破缺使其能夠存儲環境中持久存在的多樣性來源。
在1987年的論文《自旋玻璃哈密頓量:生物學、統計力學和計算機科學之間的橋樑》(Spin glass Hamiltonians: a bridge between biology, statistical mechanics, and computer science)中[15],安德森強調了哈密頓量在 N→∞ 極限下的相變,即系統打破遍歷性,相空間中的不同區域被 Np(其中 p < 1)階能量勢壘分隔開。自旋玻璃是解決耗散結構尺度依賴敏感性的最簡單的平衡系統,它將隨機波漲落“凍結”為穩定的凝聚態。這個特性直接導致了所有生命系統的一個基本經驗特徵,即第三個安德森原則——自主性。
3. 自主性
普里高津強調了由小波到平均狀態產生的耗散結構的尺度依賴性[13],以及這些波動如何增長到受系統長度限制的幅度。其中許多更有説服力的例子來自流體動力學,包括上述的對流現象,以及氣旋、颶風和B-Z振盪反應。最近的研究人員聲稱所有生命結構都是耗散結構,或者是“生物類耗散結構”(參見[16]進行的最新綜述)。儘管這是一個非常有趣的想法,並且無疑是解釋適應性形態起源的部分答案,但安德森的敏鋭批評不僅僅侷限於這一點,他還指出了一種更為微妙和功能上重要的缺陷——缺乏自主性[5]。正如安德森所述,“自主結構的自主性是指其空間或時間結構不應在外部邊界條件的尺度上預先確定”。自主性是所有複雜生命形式的重要特徵,跳蚤中的細胞不比大象中的細胞更小,呼吸複合物在所有生命形式中的結構和尺度都是相同的,基因的長度不取決於它們所在的細胞或有機體的大小。這個列表可以無限擴展。
在簡單物理設備(如激光器)以上的尺度上,真正生成“自主的”耗散結構非常困難,因為它們的功能與物理定律相差不遠。耗散結構的最初概念出現在艾倫·圖靈(Alan Turing)的形態發生理論中[17],除了顯示出對域尺寸極度敏感之外,還存在“微調”問題,即穩定的駐波需要對形態生成物的擴散性進行相當精確的調節(參見[18]和[19]中的分析和可能的解決方案)。已經有人嘗試將反應擴散系統應用於生物現象,例如魚皮的條斑形成,但正如研究人員指出的,還需要額外的非耗散性記憶來源來克服由特定參數值引起的固有空間波長[20]。
安德森認為耗散動力學在對稱性破缺方面起着關鍵的早期作用,並隨後被凝聚成準平衡模式。在形態發生領域,這對應於由漲落驅動的不穩定性產生圖靈斑圖,然後通過遺傳調控網絡(長期記憶)在一定延遲後得到鞏固[21]。
迄今為止,形態發生斑圖(pattern)在動力學上具有關鍵作用。即使耗散結構可以在保持生長敏感性的同時穩定並實現尺度無關,這遠遠不能滿足完整體積斑圖發揮任何有用機械工作的要求。這引出了安德森提出的第四個原則——廣義剛性。
4. 廣義剛性
剛性通常被定義為固體在承受機械應力時抵抗形變的能力。詹姆斯·克拉克·麥克斯韋(James Clerk Maxwell)在他的論文《論可易圖形和力圖》(On reciprocal figures and diagrams of forces)中,首先探討了剛性的重要性,並與力通過一系列剛體的傳播有關[22]。幾乎我們對經典力學的所有直覺,從枱球、彈簧和槓桿,到動物運動,都涉及剛性的概念。畢竟,柔性的零件不能製造可靠的機械鐘。
安德森對所有剛性相互作用感興趣,這些相互作用使得控制參數(如温度)能夠通過應力系統傳遞其力量,從而在適當的序參量(如自旋角度)中顯現出來。任何非平凡的機制都必須具有廣義剛性,且具備以下特點:“(1)……內部自由度不能預先確定;(2)具有可以穩定操縱的自由度,並能夠實施遠程作用[5]。”
儘管剛性對於生物體或機器的運動特徵很重要,但對於信息處理同樣重要。一個明顯的例子是集成電路中的晶體管。晶體管是半導體,通過連接到固定拓撲電路的兩個端口傳輸電流而工作。如果集成電路不能可靠地傳輸電流,而是具有柔性(在這種情況下泄漏大量電流),計算將無法進行。同樣的道理也適用於電化學信號在神經系統中的傳播。一個柔性的反射動作只會變成無效的痙攣。我們之所以需要描述連接組(connectome),是因為神經元之間的連接在功能上具有信息性,因為它們揭示了電化學信號的優先傳播方式。
正如安德森在談到內部自由度的獨立性時所説的,可靠構建剛性系統的關鍵是自主部件。例如,細胞中的分子馬達利用布朗運動的棘輪原理通過剛性相互作用傳遞力,這涉及通過使用短程吸引力來捕獲有利的漲落,從而偏置或整流原本隨機的布朗運動。”這些驅動反應向前發展,通過以單體大小的步長進行,利用將單體結合在一起的能量來推動纖維和負載的波動[23]。
更基本地説,廣義剛性是因果關係的物理先決條件。休謨(Hume)將因果關係定義為可靠的原因和結果,“我們可以將原因定義為跟隨着另一個物體,並且所有與第一個物體相似的物體都跟隨着與第二個物體相似的物體。換句話説,如果第一個物體不存在,第二個物體就永遠不存在。”正如 Halpern 所言[24],剛性使得既有規律性(A然後B)的概念又有反事實(非A然後非B)成為合理的。

「 結語:對稱性、信息和演化 」
為了説明問題,我給這安德森四原則打上了標籤,它們擴展了我們對對稱性和對稱性破缺在複雜系統中所扮演的關鍵角色的理解。我發現這些原則是對相變與湧現性、耗散結構與適應性特徵,以及斑圖形成與機械和計算工作之間關係的許多有疑問的思考的糾正。我有時把它們看作是一個最小的核對清單,以確保任何提出的機制都不僅僅是一個有趣的模式。圖1以隱含的順序説明了這四個原則。
安德森沒有深入探討的兩個領域是信息論和演化,這兩個領域是從他對湧現現象的研究自然延伸來的。信息論可以説是任何測量複雜性的努力中最有效的理論基礎(超越簡單的對稱性破缺),演化則是所有領域中以對稱性破缺為基礎概念的頂峯——更經常被描述為“凍結的偶然事件”。
信息熵畢竟是一種用於計算對稱性破缺的計數統計量(在20個問題中的每一個是與否的回答都減少了置換羣的基數)。通過突變——漂移——選擇的方法來簡約重建譜系樹,將性狀置於根部位置以最小化對稱性破缺(Hennig輔助原則)。最大熵方法假設對稱性,以便在其身上施加約束或打破對稱,這些約束或破缺對稱可以通過與數據擬合進行約束[25]。而一般地,複雜性可以看作是與可觀測變異一致的最簡歷史[26]——換句話説,最對稱(例如可並行)的過程,可以將隨機輸入轉化為規則輸出[27]。
參考文獻
Weyl H. 1952 Symmetry. Princeton, NJ: Princeton University Press.Anderson PW. 1972 More is different. Science177, 393-396. (doi:10.1126/science.177.4047.393)Anderson P. 2005 The eightfold way to the theory of complexity: a prologue. In A career in theoretical physics, pp. 779-787. Singapore: World Scientific.Buhse T, Cruz JM, Noble-Terán ME, Hochberg D, Ribó JM, Crusats J, Micheau J-C. 2021 Spontaneous deracemizations. Chem. Rev.121, 2147-2229. (doi:10.1021/acs.chemrev.0c00819)Anderson PW. 1994 Some general thoughts about broken symmetry. In A career in theoretical physics, pp. 419-429. Singapore: World Scientific.Landau L. 1936 The theory of phase transitions. Nature138, 840-841. (doi:10.1038/138840a0)Schrödinger E, Penrose R. 2012 What is life? Cambridge, UK: Cambridge University Press.Ribó J, Hochberg D. 2019 Chemical basis of biological homochirality during the abiotic evolution stages on earth. Symmetry11, 814.Kauffman S. 1974 The large scale structure and dynamics of gene control circuits. J. Theor. Biol.44, 167-190. (doi:10.1016/S0022-5193(74)80037-8)Laughlin RB, Pines D, Schmalian J, Stojković BP, Wolynes P. 2000 The middle way. Proc. Natl Acad. Sci. USA97, 32-37. (doi:10.1073/pnas.97.1.32)Ay N, Krakauer DC. 2006 Geometric robustness theory and biological networks. Theory Biosci.125. 93-121. PubMed, ISI,Anderson PW. 1983 Suggested model for prebiotic evolution: the use of chaos. Proc. Natl Acad. Sci. USA80, 3386-3390. (doi:10.1073/pnas.80.11.3386)Prigogine I. 1978 Time, structure, and fluctuations. Science201, 777-785. (doi:10.1126/science.201.4358.777)Hopfield JJ. 1982 Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA79, 2554-2558. (doi:10.1073/pnas.79.8.2554)Anderson PW. 2018 Spin glass Hamiltonians: a bridge between biology, statistical mechanics and computer science. In Emerging syntheses in science, pp. 17-20. Boca Raton, FL: CRC Press.Kondepudi DK, De Bari B, Dixon JA. 2020 Dissipative structures, organisms and evolution. Entropy22, 1305. (doi:10.3390/e22111305)Turing A. 1952 The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B237, 37-72. (doi:10.1098/rstb.1952.0012)Fuentes MA, Krakauer DC. 2007 The evolution of developmental patterning under genetic duplication constraints. J. R. Soc. Interface5, 237-245. (doi:10.1098/rsif.2007.1074)Butler T, Goldenfeld N. 2011 Fluctuation-driven Turing patterns. Phys. Rev. E84, 011112. (doi:10.1103/PhysRevE.84.011112)Höfer T, Maini PK. 1996 Turing patterns in fish skin? Nature 380, 678. (doi:10.1038/380678b0)Gaffney EA, Monk NAM. 2006 Gene expression time delays and Turing pattern formation systems. Bull. Math. Biol.68, 99-130. (doi:10.1007/s11538-006-9066-z)Maxwell JC. 1864 XLV. On reciprocal figures and diagrams of forces. Lond. Edinb. Dublin Philos. Mag. J. Sci.27, 250-261. (doi:10.1080/14786446408643663)Oster G. 2002 Brownian ratchets: Darwin’s motors. Nature417, 25-25. (doi:10.1038/417025a)Halpern JY. 2017 Actual causality. Cambridge, MA: The MIT Press.Jaynes ET. 1957 Information theory and statistical mechanics. Phys. Rev.106, 620-630. (doi:10.1103/PhysRev.106.620)Prigogine I. 1987 Exploring complexity. Eur. J. Oper. Res.30, 97-103. (doi:10.1016/0377-2217(87)90085-3)Bennett CH. 1988 Logical depth and physical complexity. In The universal Turing machine, a half century survey (ed. Herken R), pp. 227-257. Oxford, UK: Oxford University Press.
本文經授權轉載自微信公眾號“集智俱樂部”。
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。