求教丨為一位小學生創造的“多集合容斥取極值問題”的新解法作一個規範表述遭遇的難題_風聞

**按：**此前在風聞求教了一道“多集合容斥取極值問題”（見：求教丨一道貌似淺灘實則深淵的小學數學燒腦題：多集合容斥取極值問題），得兩位高人（尤其難得的是其中一一位是個小學生）賜教，給出了一種與主流解法（“反向、求和、作差”）迥異的新解法。但在深入解析該創新解法也即試圖為該解法作一規範表述的過程中，我又遇到了難題，在關節處找不到恰切的語言表述使其邏輯嚴謹、通暢。為此，再次發帖求助，盼高人賜教。

----------------------------------

題曰：

某班有60人，其中：43人會騎車，45人會游泳，50人會溜冰，48人會足球。問：至少有幾人四項都會？

小朋友給出的思路及其解法是（孩子家長的轉述）：

我兒子想到一個思路，每個學生四個技能槽，假設所有人都填滿了三個技能槽，這時候還有43+45+50+48-60*3=6個技能沒有分配，所以還必須有六個人的技能槽填滿。

小朋友獲得他的思路的方式是（孩子家長“bluekylin ”的轉述）：

他説他剛學過抽屈原理，感覺可以用這個思路。

另一位是成人，風聞ID“相約酒吧”，他給出解法與小朋友的異曲同工，表述稍有不同：

每人會3項最多180項，現在共186項，那肯定至少6人會4項，哪用那麼複雜？

我對這一創新思路及其解法中的細節很感興趣，於是分別請教了這兩位高人，小朋友沒有為他的思路和解法作更深入的解析（孩子家長未有轉述），“相約酒吧”倒是作了一些解釋：

1、這不應該是最符合直覺的解法嗎？儘可能減少4項的人數就等於儘可能多掌握3項的人啊。

2、最極端情況下沒有一個人會四項，那最多會多少項？然後在給定條件下，要增加多少會4項的人，不就很清楚了。你要靠教別人孩子套用工具去應付奧賽來賺錢，所以覺得你自己的那些套路很重要。會這些套路可能能拿個華盃賽金獎，但是對篩選真正的尖子沒啥用。

另有一位“cchere”學友也給出了一個解釋説明：

假設沒有一個人會四項，60個人合計最大值為60*3為180。而四項合計值為186，則顯然至少有6人會四項，否則不可能超過180。

無論是小朋友的原始表述還是“cchere”和“相約酒吧”給出的解釋説明，本來似乎都已經一聽即明瞭，我也感覺自己理解了。但是，當我試圖深入細節並將其用規範表述闡釋清楚時，我遭遇了語言表述上的困難。

以下是我所作表述的初始版本：

設定每人都有4個“技能槽”且初始狀態均為“空”待“充值”，若假設沒有一人的4個“技能槽”全部被“充值”，則當每人的4個空“技能槽”中的3個均被“充值”時，所有人的被“充值”的“技能槽”數量之和最多，該最多數量為60×3=180（個）；

而實際所有人的被“充值”的“技能槽”數量之和為43+45+50+48=186（個），比假設情況多186-180=6（個）；

則説明實際上還有6個“技能槽”被“充值”，而假設情況下所有人都僅有1個“技能槽”為空，所以有6人各自餘下的1個空“技能槽”被“充值”，這樣，就有6人的4個空“技能槽”均被“充值”；

由於，………………

故，此6人即為4個空“技能槽”均被“充值”的人數的最小值。

也即：4個空“技能槽”均被“充值”的至少有6人；

故，至少有6人四項都會。

----------------------------------------------

【注：“……”這裏又是一個“鴻溝”，左思右想找不到一個恰切的表述將其中的邏輯呈現出來】

以下是兩個修改版本：

其一

設定每人都有4個“技能槽”且初始狀態均為“空”待“充值”，若假設沒有一人的4個“技能槽”全部被“充值”，也即4個“技能槽”未被全部“充值”的人數取最大值即全部60人，則當每人的4個空“技能槽”中有且僅有3個均被“充值”時，所有人的被“充值”的“技能槽”數量之和最多，該最多數量為60×3=180（個）；

而實際所有人的被“充值”的“技能槽”數量之和為43+45+50+48=186（個），比假設情況多186-180=6（個），這説明實際上還有6個“技能槽”被“充值”，又由於假設情況下所有人都僅有1個“技能槽”為空，所以這6個被“充值”的“技能槽”分別一一對應於6個人的各自餘下的1個空“技能槽”，也就是説，有6人的4個空“技能槽”均被“充值”；

這樣，實際情況下4個空“技能槽”中有且僅有3個均被“充值”的人數相對於假設情況下的人數的最大值即所有/全部的60人要少6人，也就是説，4個空“技能槽”中有且僅有3個均被“充值”的人數的最大值為60-6=54（人），所以，4個空“技能槽”均被“充值”的人數的最小值為6人；

也即，至少有6人四項都會。 

----------------------------------------

【注：該表述在邏輯上仍然不嚴謹、不通暢，其中關鍵處在於，沒有找到恰切的表述方式將實際比假設多出的6個被“充值”的“技能槽”與4個空“技能槽”均被“充值”的人數“‘至少’有6人”嚴密對應起來，具體説就是兩點，其一，如何將實際被“充值”的“技能槽”比假設多出的6個解釋為/對應到某種意義上的“‘至少’6個‘技能槽’”，其二，如何將“‘至少’6個‘技能槽’”解釋為/對應到“‘至少’6個‘人’”。（“6個‘技能槽’”對應“6個‘人’”比較好解釋、容易建立一一對應，但加入“至少”的限定描述後其間的“一一對應”關係就不太好解釋、表述了）】

——引自：“創新就是孩子的遊戲”！親見案例讓我更堅信：孩子本有創新所必須的豐富的想象力和敏鋭的直覺，老師和家長應對其予以精心呵護並善加滋養

其二

假如沒有人“四項全會”，也即全部60人中“‘四項全會’者”人數為0，則當全部60人每人都會三項（即每人不會的僅僅只有某一項）時，全班所有人所會“‘項次’數”（“項次”可類比於“人次”來理解）的總和取到最大值，該最大“‘項次’數”為：60×3=180（項次）；

而所有人實際所會“‘項次’數”為：43+45+50+48=186（項次）；

實際比假設多出的“‘項次’數”為：186-180=6（項次）；

由於假設情況下全部60人每人已經都會了三項即每人僅有一項不會，則實際比假設多出的6項次分別一一對應於6個人各自所僅不會的一項，這就導致實際上至少有6人“四項全會”了；

也就説，實際比假設需要至少6個人“四項全會”；

故，至少有6人四項全會。

-------------------------------------------

【注：該表述在邏輯上仍然不嚴謹、不通暢，其中關鍵處在於，沒有找到恰切的表述方式將“實際比假設多出的6個‘項次’”與“‘四項全會’者‘至少’有6人”嚴密對應起來，具體説就是兩點，其一，如何將實際比假設多出的6個“項次”解釋為/對應到某種意義上的“‘至少’6個‘項次’”，其二，如何將“‘至少’6個‘項次’”解釋為/對應到“‘至少’6個‘人’”。（“6個‘項次’”對應“6個‘人’”比較好解釋、容易建立一一對應，但加入“至少”的限定描述後其間的“一一對應”關係就不太好解釋、表述了）】

——引自：“創新就是孩子的遊戲”！親見案例讓我更堅信：孩子本有創新所必須的豐富的想象力和敏鋭的直覺，老師和家長應對其予以精心呵護並善加滋養

各個表述之後的“【注】”中對我遭遇的表述難題作了詳細描述，我不知道各位是否把握到我描述的“難題”，或者，我描述的這個“難題”究竟是個“真問題”中的“難題”還是是個“假問題”中的“難題”。是我沒事找事自討苦吃（庸人自擾）呢，還是其中卻有問題被我意識到了（但不能明晰地表達出來）？

盼高人賜教（另，特別懇請“相約酒吧”、“cchere”、“bluekylin ”和他兒子、“雲胡不喜”幾位先前已有賜教高見的幾位學友再次賜教）。

-----------------------------------------

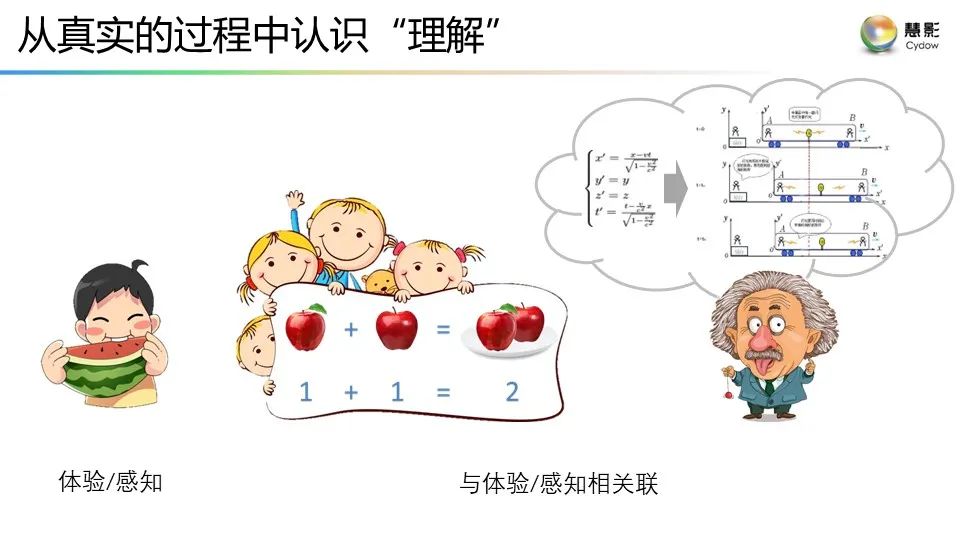
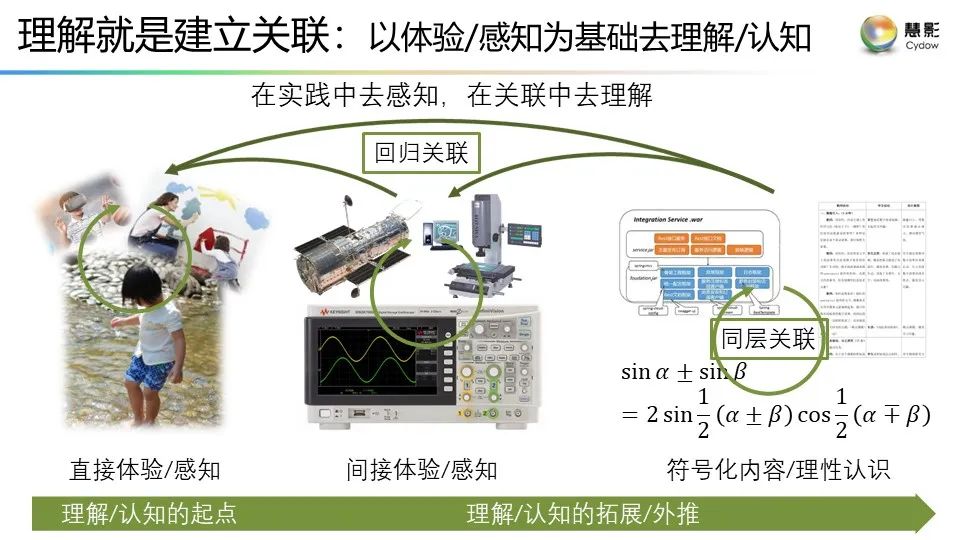
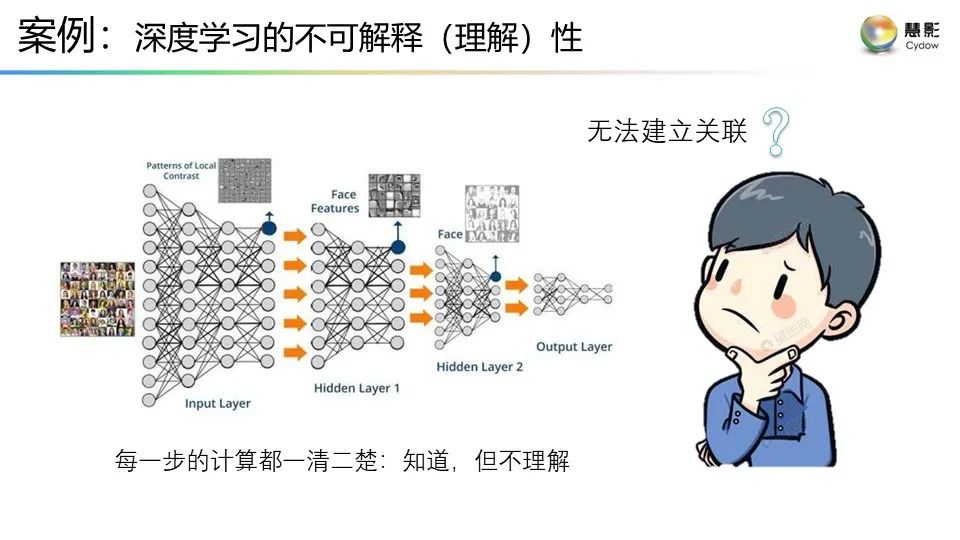
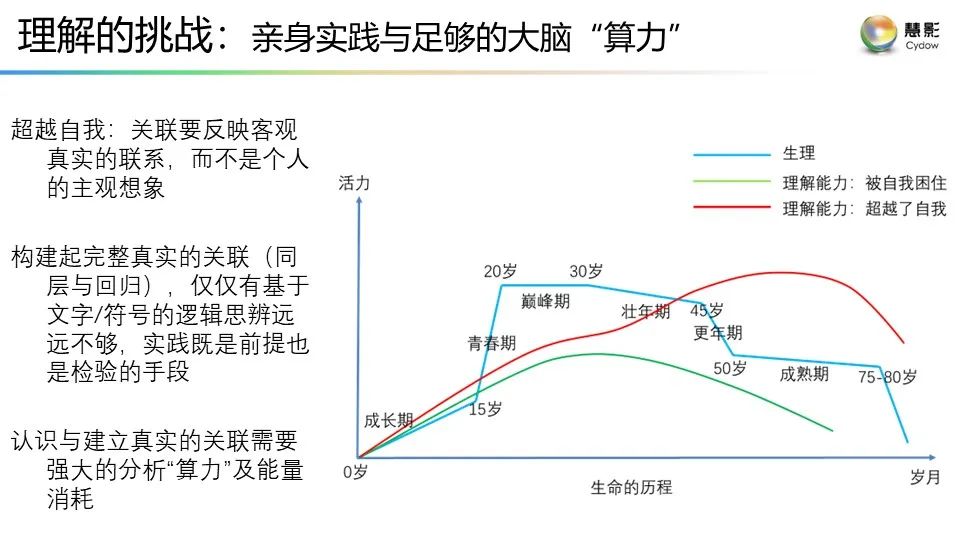
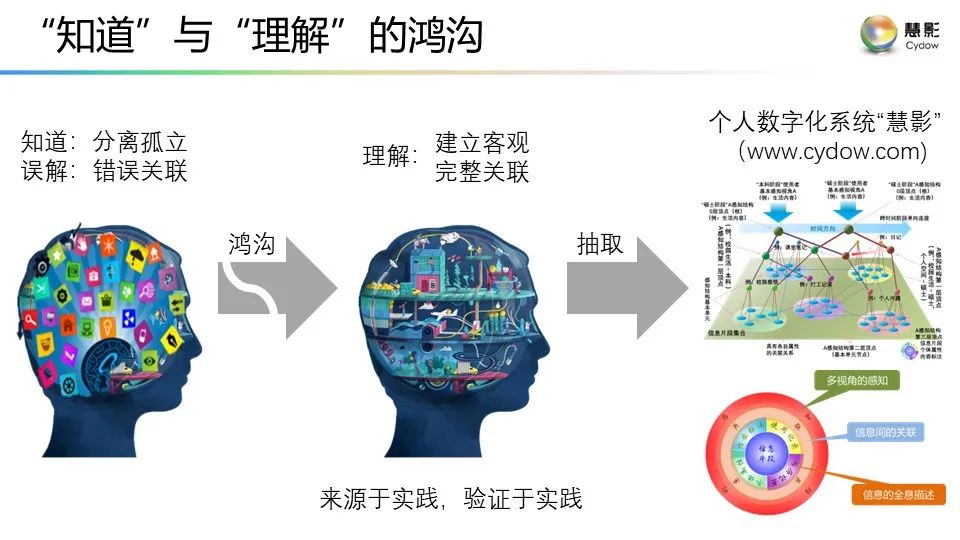
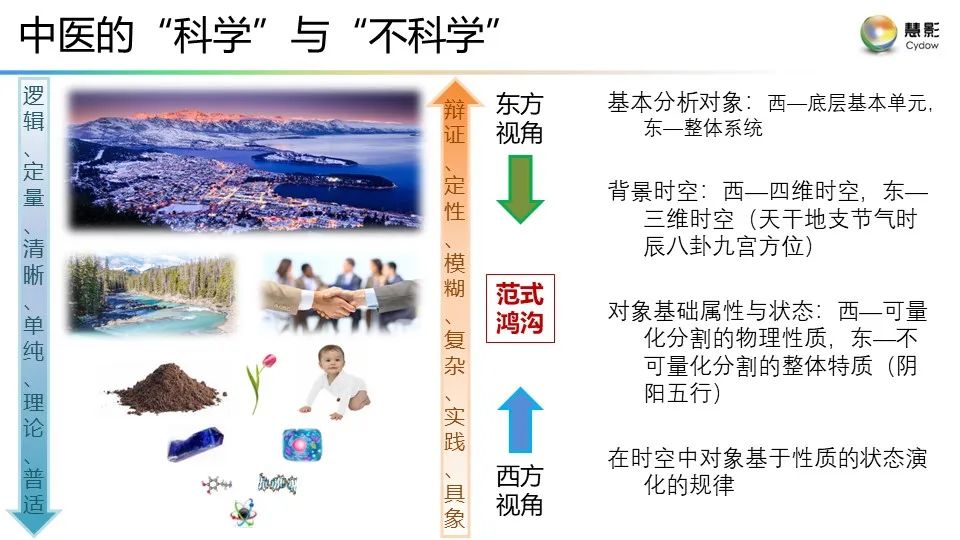
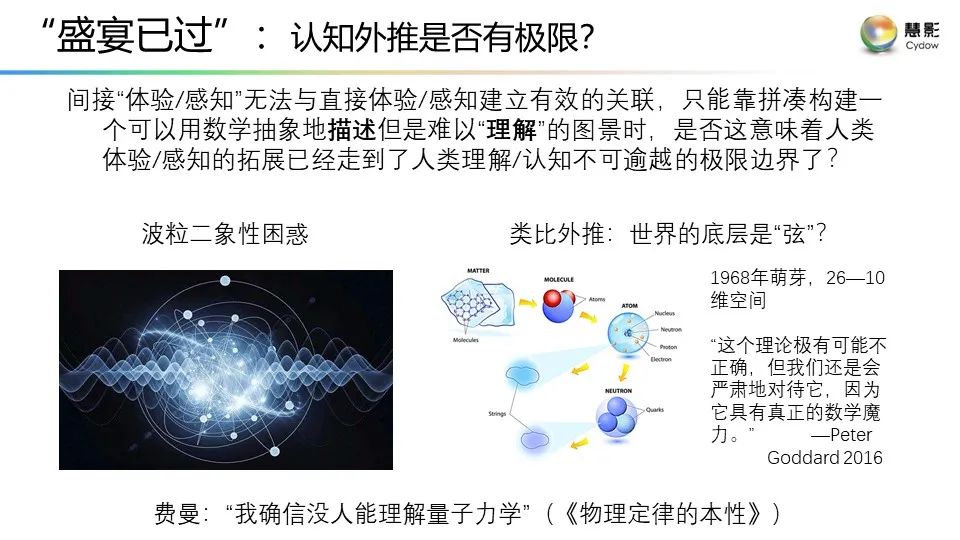
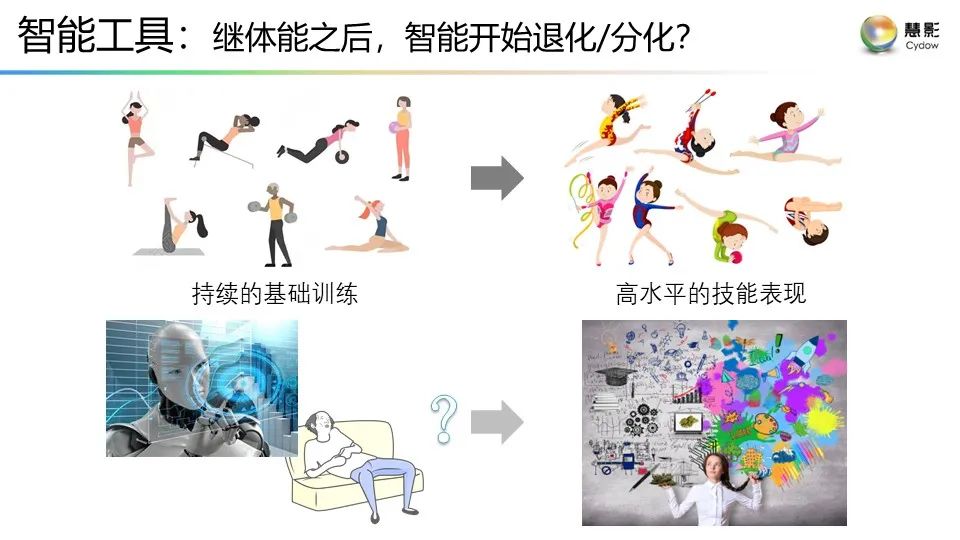
**附：**謝耘《理解之理解》演講的視頻鏈接以及PPT

視頻鏈接：謝耘：“理解”之理解

PPT