超越海森伯極限的量子精密測量_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!06-29 10:29
撰文 | 陳耕、李傳鋒(中國科學技術大學 中國科學院量子信息重點實驗室、中國科學技術大學 合肥國家實驗室)
來源 | 選自《物理》2023年第6期
01 理論密碼
不斷提升測量精度是科學研究發展的一個源動力。科學技術發展到今天,很多里程碑式的進步都得益於測量精度的提升。一個眾所周知的例子是2016年引力波的成功探測[1],驗證了愛因斯坦廣義引對論的預言。然而從激光干涉引力波天文台 (LIGO) 建成到第一次探測到引力波整整花了17年時間,這是科學家們不斷改進裝置以提升探測精度的結果。最近科學家們在引力波探測中使用了量子壓縮的光源,進一步提升了探測精度,使得現在幾乎每週都可以觀測到引力波。
用新的原理方法、技術手段提高測量精度,本身就是自然科學研究的一個重要方向,我們稱之為精密測量研究。科學界一般使用測量的不確定度Δ隨所使用的測量資源N的下降速率來刻畫一個測量系統的測量能力。經典方法能達到的極限是Δ隨N的0.5次方成反比下降,也就是我們所稱的標準量子極限 (standard quantum limit) 。需要注意的是,雖然名字中帶有“量子”,但是這個下降速率是經典方法能達到的極限。如果能把測量中所有的技術噪聲都壓制到很低,從而使量子漲落成為主要噪聲,就可以達到這個極限。但是在實際測量場景中,起主導作用的經常是各種技術噪聲,這時放大信號提升信噪比是一個提升最終精度的有效途徑。一個典型的方法是“弱測量”方法,它可以後選擇 (post-selection) 出移動幅度最大的一小部分探針,從而將信號放大100倍甚至1000倍以上。中國科學技術大學研究團隊使用了一種改進型的偏置弱測量方法,在放大信號的同時大幅降低了探測器的光電飽和效應,相比標準弱測量方法的探測精度又提升了一個數量級[2]。但是這種弱測量方法並不能超越標準量子極限,因為它本質上是經典光的干涉效應。
02 量子精密測量
量子精密測量是最近十年來在量子信息研究中一個蓬勃發展的領域,旨在利用量子的方法和資源實現突破標準量子極限的測量精度。如前所述,引力波探測裝置使用量子壓縮光之後可以實現超過標準量子極限的測量精度,這充分證明了量子精密測量的可行性和重要性。那麼一個對於量子力學本身的理解和實際測量精度都很重要的問題是:量子精密測量可以提供的精度極限在哪裏?實際上對於這個問題,海森伯在1927年就給出了很好的答案,也就是海森伯不確定原理。它是量子力學的一個基本原理,根據這個原理給出的最高測量精度我們稱之為海森伯極限:即測量的不確度Δ與N的1次方成反比下降。
因此,量子精密測量的一個重要任務是發明新的方法和量子資源來逼近這個極限。光或原子的壓縮態不可能達到這個極限,因為實際實驗中壓縮比總是有限的。一個原理上可以達到這個極限的方法是使用多體糾纏態,比如在量子信息中常使用的N00N態,它通常具有如下的形式:
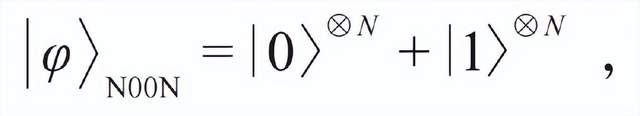
2018年,來自於中國科學技術大學的研究團隊發展了一種量子化的新型弱測量方法。這種方法用光子數的混態作為探針,以單光子的量子疊加性作為量子資源,實現了對單光子克爾效應反比於N的1次方的測量精度,反比係數約為6.2[3]。該工作的最好精度相當於使用N = 100000的N00N態可以達到的效果,並優於之前最好的經典方法[4]一個數量級。不久後,該團隊又通過使用單光子投影測量代替混態探針,實現了逼近海森伯極限的測量精度,反比係數進一步降低到了1.2[5]。其最好精度相當於使用N = 1000000的N00N態可以達到的效果,並優於之前最好的經典方法[4]兩個數量級。雖然是在一個特定的測量任務中進行的,但是這兩個工作首次實現了在實際測量任務中達到海森伯極限並優於經典方法,充分展現了量子精密測量的優勢。
海森伯極限被學術界廣泛認為是量子力學所允許的測量極限,是否有可能超越這個極限一直是學術上備受關注和存在爭議的問題。2011年,Napolitano等人的一個工作聲稱超越了海森伯極限[6],對光非線性係數測量達到反比於N的1.5次方的超海森伯極限。但是這個工作後來受到了廣泛的置疑甚至是批評[7—9],因為所使用的資源為光子通過原子團產生的經典非線性,其哈密頓量裏已經含有了N的平方項。在以所使用的總能量作為規範化資源定義的前提下,這個工作甚至沒有超過標準量子極限。
03 量子不定因果序的精密測量
近些年來,一種新的量子結構,即量子不定因果序 (indefinite causal order,ICO) 引起了學術界極大的研究興趣。量子力學顯然允許一個粒子處於不同狀態的量子疊加,比如光子可以處於不同偏振疊加態,原子可以處於不同能級的疊加態。事實上,量子力學還允許兩個演化不同的時序之間的量子疊加,這點顯然不同於經典世界的因果關係。在經典世界裏,如果兩個事情A和B之間存在關聯,那麼它們之間孰因孰果是確定的。如果A發生在B之前,那必然A是因B是果;反過來的話,就是B因A果。而在量子世界裏,兩個事件可以處於如圖1所示的兩個相反時序的量子疊加上,也就是説孰因孰果這個問題是不確定的。這樣的系統狀態可以表示為:

這樣一種新的量子結構已經被證明在各種量子信息過程中可以提供進一步的量子增強。比如降低量子計算問題中的複雜度,提升量子通信中通過信道的互信息量。尤其讓大家感覺到意外的是,2020年香港大學的一個理論工作證明[10],量子不確定因果序可以在精密測量中突破海森伯極限,達到前所未極的反比於N的2次方的超海森伯極限。這樣一個理論突破考慮了由兩組連續變量進行N次獨立演化產生的幾何相位A的測量,比如一個變量是座標空間的本徵值x,另外一個變量是動量空間的本徵值p。傳統確定因果序的方法在這樣一個測量問題中最好的精度極限是海森伯極限,可以由如圖2(a)所示的串行測量裝置達到。如果把這樣兩組演化製備到兩個相反時序的疊加上,如圖2(b)所示,就可以獲得一個隨着N2A增加的總體相位,也就是獲得了指數加速的能力,從而對幾何相位的估計可以達到反比於N2的精度,也就是超海森伯極限。
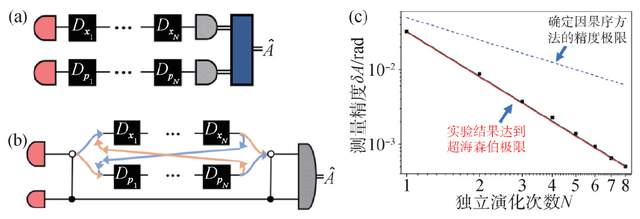
這樣一個結果在實驗實現上遇到了很大的困難,因為它同時涉及到了離散變量和連續變量體系,並且需要將這兩種體系糾纏起來,也就是利用離散的量子比特狀態去控制兩組連續變量的演化時序。量子信息方案中的離散變量體系無法實現連續變量的演化,而連續變量體系無法把兩組演化製備到兩個相反時序的量子疊加上。中國科學技術大學的團隊通過構造一種全新的雜化 (hybrid) 裝置實現了這樣一個量子結構[11],用光子的偏振狀態來控制光子橫向模式的位置和動量的演化。他們用特製的光學元件精準實現了這兩個連續變量的多步微小演化,在一個接近1 m長的馬赫—曾德爾(MZ)干涉儀的兩臂上分別實現了兩個時序相反的演化過程。實驗結果對幾何相位的測量精度可以達到如圖2(c)所示的超海森伯極限,並且優於任意確定因果序方案能達到的最高精度。
這個實驗中所使用的探針是單個光子,所以每次測量所需要的能量與N無關。在以能量為規範定義的前提下,這是目前唯一可以達到1/N2超海堡極限的實驗工作。這一點和以經典非線性作為資源的工作形成了鮮明對比。同時在這樣一個測量任務中,兩種時序所能達到的精度已經是最優的結果,用更多的時序並不能獲得更好的測量精度。這使得用光子的二維偏振就可以控制不定因果序,而不需要更高維度的離散變量。特別值得強調的是,這樣一個實驗在演示的範圍內已經實現了相對於傳統方法的絕對優勢,而不僅僅是一種潛在的優勢。因為這個實驗中N代表的是獨立演化的次數,而不是量子態的規模。如N00N態精密測量所具有的潛在優勢無法變成現實優勢,就是因為現階段量子態的規模無法做大。
04 總結和展望
一個無法避免的情況是,關於海森伯極限是否是量子力學的最終極限的爭議會一直持續下去,這主要是由學術界對測量資源定義的不統一所導致的。用量子不定因果序可以實現超海森伯極限的測量精度也必然會引起學術界的廣泛討論和爭議。但是如果我們擱置這些爭議,從一個更加現實的角度去考量這種新方法,它確實達到了比之前任何確定因果方法都要更好的測量精度,這種優勢獨立於海森伯極限該如何定義這樣一個深刻的問題。當然另外一個值得思考的問題是,不確定度反比於N的2次方是不是測量精度的極限?是否有方法可以達到更高的極限,比如反比關係是N的3次方,4次方……這仍然是一個未解之謎。
參考文獻
[1] Abbott B P et al. Phys. Rev. Lett.,2016,116:061102
[2] Yin P et al. Light Sci. Appl.,2021,10:103
[3] Chen G et al. Nature Communications,2018,9:1
[4] Matsuda N et al. Nature Photonics,2008,3:95
[5] Chen G et al. Phys. Rev. Lett.,2018,121:060506
[6] Napolitano M et al. Nature,2011,471:486
[7] Zwierz M et al. Physical Review A,2012,85:042112
[8] Berry D W et al. Phys. Rev. Lett.,2012,86:053813
[9] Hall M J et al. Physical Review X,2012,2:041006
[10] Zhao X et al. Phys. Rev. Lett.,2020,124:190503
[11] Yin P et al. Nature Physics,2023,https://doi.org/10.1038/s41567-023-02046-y
本文經授權轉載自微信公眾號“中國物理學會期刊網”。
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
