米蘭· 昆德拉教給我的科學原理|袁嵐峯_風聞
风云之声-风云之声官方账号-07-13 21:06

米蘭·昆德拉
著名文學家米蘭·昆德拉去世,享年94歲,特此紀念。我看過他的《生命中不可承受之輕》和《不朽》,從中得到的最大的震撼是:小説居然還可以這麼寫,在虛構與現實、哲理與敍事之間來回穿梭。

歌德

貝多芬
在《不朽》中他回顧了歌德與貝多芬見到貴族時相反表現的故事,卻給出了與傳統不同的解讀,甚至還設想了兩人在天堂相遇的情景。此書中還有一個地方令人忍俊不禁,他以作者的身份説有人問他最近在創作什麼作品,他説在寫《生命中不可承受之輕》。提問者納悶地説我好像聽説過這個名字,他説沒錯,就是我寫的!但我現在覺得,這個名字用在現在這部作品上更好 。
。
最奇妙的是,米蘭·昆德拉居然讓我在自然科學方面也學到了一些東西。《生命中不可承受之輕》一個反覆提到的主題是尼采的永劫迴歸,後來看了理論力學的書(如俄羅斯數學家阿諾爾德的《經典力學的數學方法》),才知道這是有科學原理的,即龐加萊迴歸定理(Poincaré recurrence theorem)。

尼采

俄羅斯數學家阿諾爾德的《經典力學的數學方法》

亨利·龐加萊
這個定理説的是:如果一個經典力學的體系滿足這樣一個條件,每個粒子可取的位置和動量都是有上限的,即整個體系的“相空間”(phase space,對於N粒子體系它是一個6N維的數學空間,其中每一個點的座標都是這個體系所有粒子的3N個座標與3N個動量的一個組合)的體積有限,那麼從這個體系的幾乎任何一個初始狀態出發(不見得所有的初始狀態都能迴歸,但那些不能迴歸的狀態即使存在,在整個相空間中所佔的比例也是0%,即它們不能構成一個體積),都會在經過充分長的時間之後,回到離初始狀態任意近的狀態(“近”指的是兩個狀態在相空間中的對應點接近,即它們的距離變得很小,小於任何一個預先給定的判據。這個距離不見得能減到0,即不一定能精確重複,但這個定理説的是:只要你預先給個“近”的判據,無論這個判據多小,都可以達到比這個判據還近,也就是説要多近都可以達到多近。當然,“近”的判據越小,所需要的迴歸時間就越長)。
這個定理的證明非常簡單,也非常巧妙,用的是反證法。經典力學滿足一個性質:相空間的體積在隨時間演化時不變經典力學滿足一個性質:相空間的體積在隨時間演化時不變(對這個性質的證明來自經典力學中的哈密頓正則方程,需要學了哈密頓力學才明白)。因此,如果我們在初始狀態附近取一個鄰域U,取一個時間步長Δt,把“演化Δt時間”作為一個操作g,那麼把這個操作反覆地作用到點集U上,就會得到一個點集的無窮序列:U, gU, g2U, g3U,……這個序列中每一個的體積都相等,都等於最初那個U的體積。那麼,它們會不會出現相交呢?

哈密頓
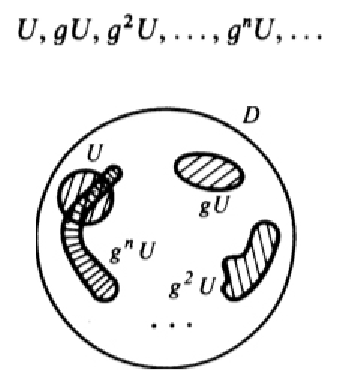
如果這些體積永遠都不相交,那麼它們的總體積會變成無限,這就和定理的條件“相空間體積有限”矛盾。因此,必然會有至少兩個區域相交,即存在兩個自然數k和m,k < m,使得gkU ∩ gmU不等於空集。
然後我們令m - k = n,把g-k作用在gkU ∩ gmU上,即讓時間倒流k步,就得到U ∩ gnU不等於空集。這就説明,U中至少有一點在n步之後又回到了U中,無論U是多小的一個鄰域。定理得證。
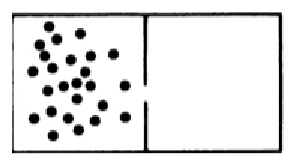
龐加萊迴歸定理是對哲學衝擊最大的物理定理之一,因為它隱含的意思是:太陽底下無新事,只要你等得夠長,任何事情都會(接近)重複地發生。如果你把一個盒子分成左右兩格,中間有個隔板,最初有一些氣體分子全都在左邊的格子裏,然後抽掉隔板,那麼常識是這些氣體分子會迅速擴散到右邊去,最後在兩邊達到平均分佈。然而龐加萊迴歸定理告訴我們,如果你等得足夠長,這些氣體分子總有一天會全都回到左邊。用熵(entropy)的語言説,就是雖然熱力學第二定律告訴我們,孤立體系的熵總是增大,不會減小,但實際上,只要你等得足夠久,熵必然會出現減小。
那麼顯而易見的問題就是,為什麼我們從來沒觀察到這種現象?回答是,理論可以推出,迴歸所需的時間隨粒子數是指數增長(可以參見李政道的《統計力學》)。所以對於稍微大一點的體系,迴歸時間就會變得比目前的宇宙年齡(137億年)還長。
但這又會引出一個問題:整個宇宙是否滿足龐加萊迴歸定理?整個宇宙會不會迴歸?答案非常奇妙,還不確定。
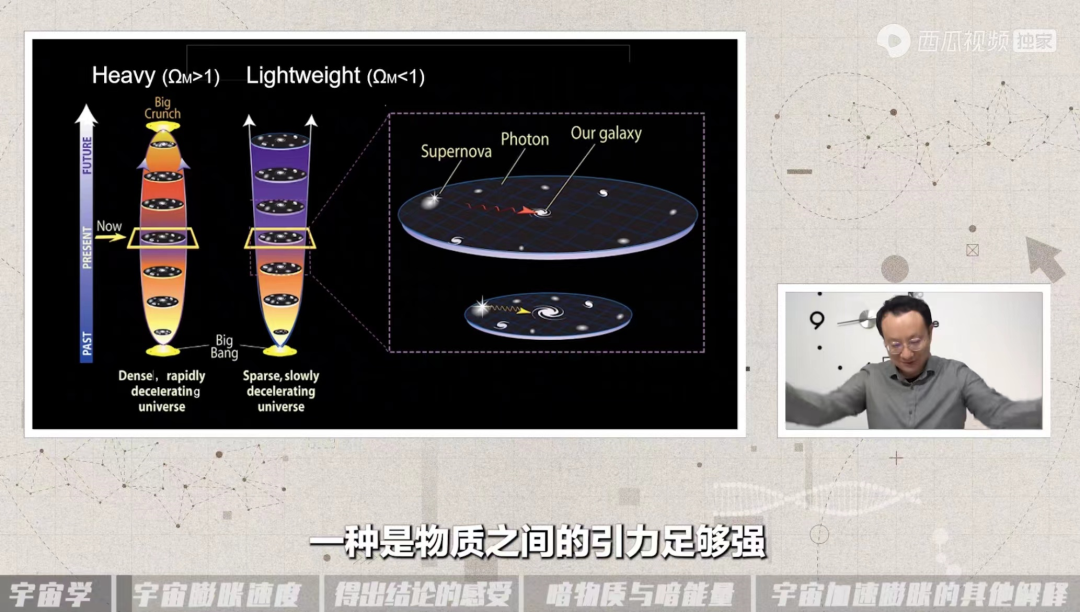
以前的標準看法是,宇宙在膨脹,所以它不滿足龐加萊迴歸定理的條件“相空間體積有限”。實際上由於膨脹,宇宙中可容納的熵也在增長,它增長得比宇宙的總熵還要快。
然而這只是以前的標準看法。自從1998年發現宇宙的加速膨脹以來(諾獎對話Adam Riess(一):宇宙膨脹不斷加速,不只有暗物質在作祟|袁嵐峯),又有人認為加速膨脹會導致宇宙最外圍的部分膨脹速度超過光速,於是我們就再也觀察不到它了,這會導致與我們有相互作用的那部分宇宙反而變得有限,即出現一個類似黑洞的“視界”(event horizon)。結果是,加速膨脹又會導致宇宙滿足龐加萊迴歸定理。不但是太陽底下無新事,而且是整個宇宙無新事!
不過,這些都只是理論設想,遠沒有確定的結論。宇宙會不會迴歸?會不會在另一個宇宙裏,也有一個米蘭·昆德拉,他正在探討尼采的永劫迴歸?這仍然是引人遐思的問題。