interesting，very interesting_風聞

首發於公眾號“賊叉”

那天看到老朋友發了這麼個題：

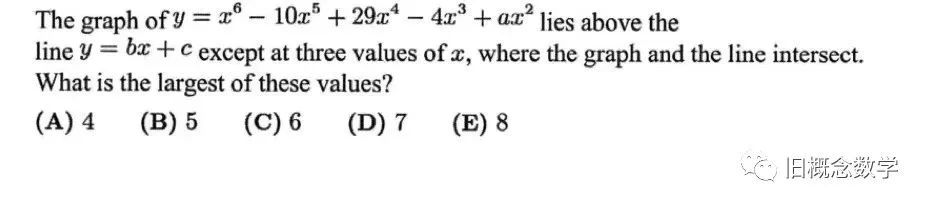
自己動了一下筆，覺得真是個好題，打算講講。

題目的意思是函數y=x^6-10x^5+29x^4-4x^3+ax^2的圖像除了和y=bx+c在三個點相交以外，其餘都位於直線的上方，求三個交點中的x的最大值。

為什麼説這是個好題？因為對初中各個年級都有借鑑意義。

初三的同學可以從頭開始看。六次函數顯然是沒有接觸過的，但是這又是個初中的題，所以一定是化歸。注意看，六次函數的圖像除了三個點以外都在直線上方，意味着什麼？

想一想，仔細想一想。

六次的不會，二次的會不會？二次函數的圖像（拋物線）始終在一條直線上方是什麼情況？

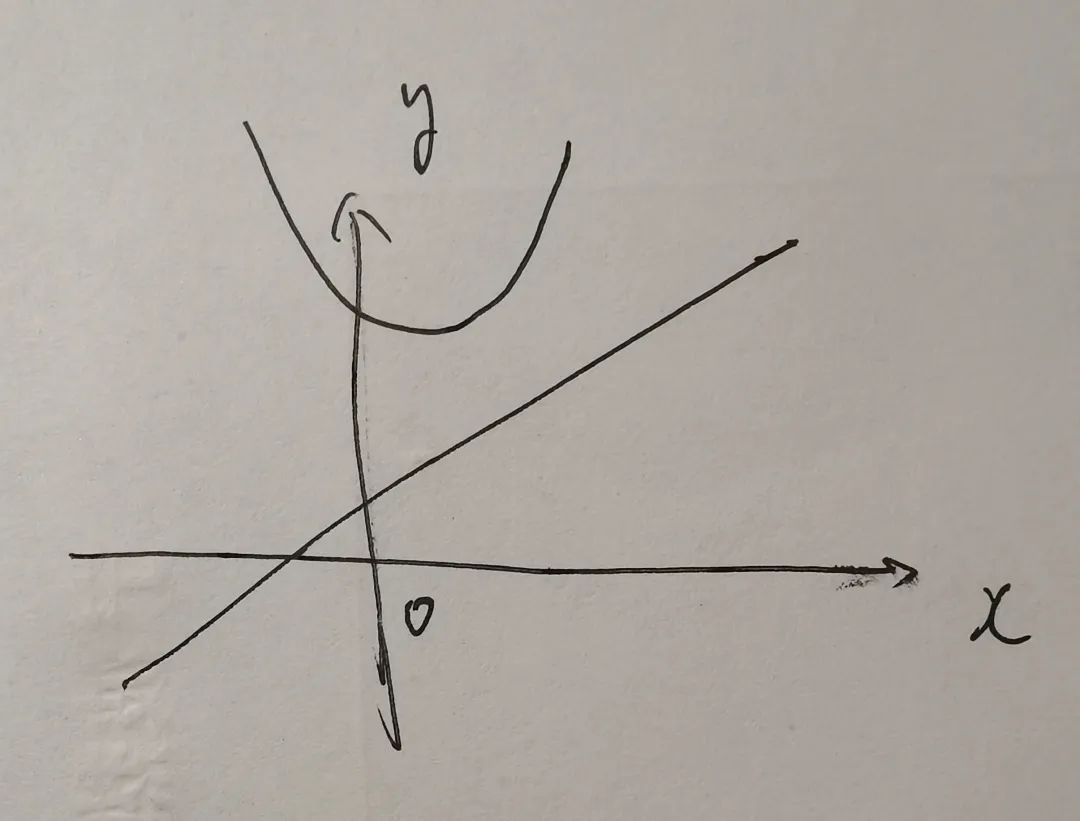
不就是這樣嘛！這意味着二次函數和直線的表達式聯立之後得到的方程沒有實根。但是注意到題目中説到六次函數的圖像和直線僅僅有三個交點，而且整體在直線上方，對於二次函數和直線來説，什麼情況最類似呢？

相切！即直線和拋物線相切，此時有且僅有一個交點，並且拋物線在直線上方。換句話説，此時題目轉化為x^6-10x^5+29x^4-4x^3+ax^2=bx+c這個方程有且僅有三個根，並且x^6-10x^5+29x^4-4x^3+ax^2≥bx+c恆成立。

然而有意思的是，題目只問你最大根是多少，但是對a,b,c的值隻字不提——這意味着a,b,c的值可能不是那麼重要（這個需要後面的解題過程來驗證）。那麼六次方程為什麼恰好有三個根呢？合理的解釋的就是這個六次方程可以寫成一個三次多項式的完全平方，而這個三次多項式恰好有三個根。

你看，我們沒接觸過六次函數，但是對二次函數和一元二次方程相對比較熟悉，現在就是不斷通過化歸的思想把原題變成了一個二次方程相關的問題。

那麼這個三次多項式應該是什麼樣的呢？注意到這個六次多項式已經有了四項的係數，所以用待定係數法是不是很自然的一件事？

我們不妨設x^6-10x^5+29x^4-4x^3+ax^2-bx-c=(x^3+px^2+qx+r)^2=0，這時候只要對比兩邊係數（事實上只要對比前四項即可），很容易解得p=-5,q=2,r=8，於是x^6-10x^5+29x^4-4x^3+ax^2-bx-c=(x^3+px^2+qx+r)^2=0=(x^3-5x^2+2x+8)^2，解得x=-1,2和4，即選A。

題目做完，同時驗證了我們之前的判斷也是對的，即a,b,c三個參數的值對解題沒有任何影響。這個題目把函數的圖像、方程的根、待定係數法、因式分解考了個遍，也就是我們所謂的綜合題了。

作為初三的學生，理論上整個過程都可以解決——當然，理論上。作為初一學生的家長，可以把前面函數部分可以略去，對題目做改編如下：

已知一元六次方程x^6-10x^5+29x^4-4x^3+ax^2=bx+c有且僅有三個二重根，求最大的二重根是多少？

這種好題做一個，真是比機械地練二十個普通題效果要好得多的多——前提是要講透、吃透。