陶哲軒發新論文了，又是AI幫忙的那種_風聞

　　豐色 發自 凹非寺

　　量子位 | 公眾號 QbitAI

　　不到一個月的時間，陶哲軒又一篇論文上線：

　　這次是關於歐拉函數的單調非遞減序列，他通過初等論證證明了一個名為M(x)函數的漸近式。

　　（即隨着x增大，M(x)的行為趨勢）

　　該函數在他之前的一篇博客中有所提及，大意是指一系列從1到x的數字中，滿足歐拉φ函數是非遞減的最長子序列的長度。

　　毫不意外，這篇論文的出產過程中也用到了AI。

　　不過，這次陶哲軒承認：

　　AI工具對他的核心研究並不那麼有用（但他也表示可能是不想打破一些已有習慣去嘗試）。

　　對他幫助最大的其實是編碼和生成論文中的流程圖****初稿。

　　對於前者，陶哲軒已多次提及。

　　GPT可以讓我不用去管計算任務中究竟用的是何種語言（Python還是SAGE、regex等），幾乎只需用自然語言向它提出請求，它就能為我輸出合格的代碼（儘管我還得再編譯一下）。

　　這真的開始改變我的工作流程。

　　過去由於我害怕困難，一直避免使用代碼密集型的任務解決問題；現在，這種情況正在消失，我發現我變得願意在日常工作中做一些編碼。

　　那麼，就來簡單看看這次的論文究竟説了什麼。

　　準備長腦子了咳咳。

　　歐拉函數的單調非遞減序列

　　該論文研究主要涉及函數M(x), 它定義的是數字1到x的最長子序列的長度，在這個子序列中，歐拉函數ψ是非遞減的。

　　（歐拉函數ψ(n)通常用於表示小於或等於n的正整數中與n互質的正整數的數量）

　　由於M的前幾個值是：

　　1, 2, 3, 4, 5, 5, 6, 6, 7, 7, 8, 8, 9, 9, 10, 11, 12, 12, …

　　所以，舉個例子：

　　M(6)就等於5。

　　因為歐拉函數在集合{1,2,3,4,5}或{1,2,3,4,6}上是非遞減的，在{1,2,3,4,5,6}上不是。

　　而由於對於任何素數p，ψ(p)=p-1，我們有M(x)≥π(x)。

　　其中π(x)是素數計數函數（用於表示小於或等於x的正整數中的素數的數量）。

　　根據經驗，這些素數非常接近M(x)的最大長度；Pollack, Pomerance和Treviño已通過數值計算推測出下式

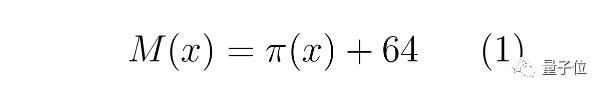
　　中的x=10⁷ 。

　　相比之下，以前最著名的上限基本上是以下形式：

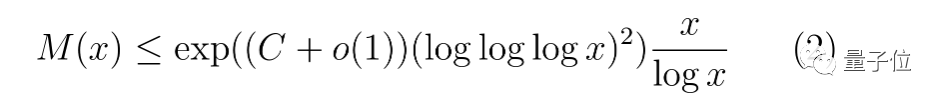
　　對於該式子，在顯式常數C=0.81781中，x→∞。

　　而將該結果與上面的結果相結合，陶哲軒就得到了漸近式：

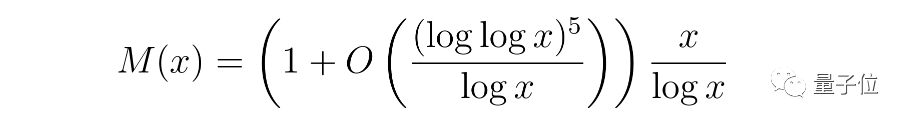
　　所以在特殊情況下：

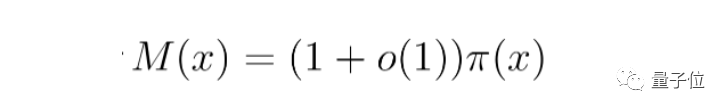
　　它既回答了Erdős的問題，也回答了與Pollack, Pomerance和Treviño所密切相關的問題。

　　陶哲軒介紹，該證明所用方法大多數都很基礎（解決數論中最先進結果所需的只是帶有經典誤差項的素數定理）。

　　基本思想是隔離給定數字1≤n≤x中的一個關鍵素因子p，因為它對歐拉函數有相當大的影響。

　　例如，對於“典型”數字n，可以因式分解為：

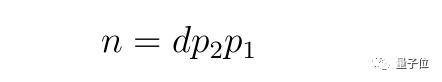
　　其中p2是中等大小的素數，p1是明顯更大的那個，d則是一個所有素數因子均小於p2的數。這可得出：

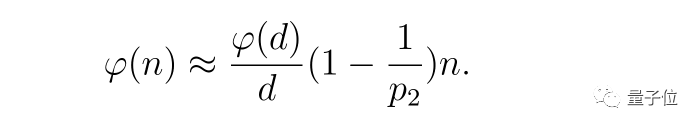
　　因此，如果我們暫時保持d固定，並將n定位到相對較短的區間，那麼ψ只能在n中是非遞減的——如果p2也同時非遞減。

　　事實證明，特別是在p2很大的情況下，這個方式顯著減少了該機制中非遞減序列的可能長度。

　　這個過程可以形式化，達成方式是通過將p的範圍劃分為各種子區間並檢查它 (以及ψ上的單調性假設)如何約束與每個子區間相關聯的n值。

　　而當p2很小時，我們使用因式分解：

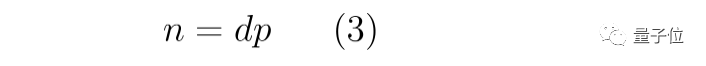
　　其中d非常“平滑”（即沒有大素數因子），而p是大素數。我們得到近似值：

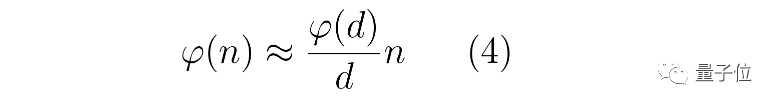
　　並得出結論：為了使ψ不變小，約等式右邊的分數基本上必須是分段常數。

　　再進行一番更仔細的分析之後，我們就能證明初步不等式，最終對於所有正有理數q得到主要定理：

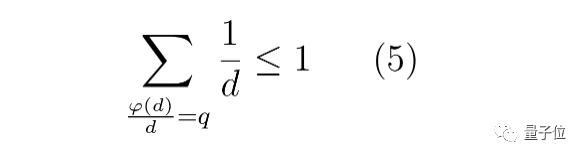
　　陶哲軒表示，這其實是一個“小奇蹟”，與以下事實有關：

　　公式(4)中分母的大質因數最低項必然等於d的最大質因數，這使得我們能夠非常準確地得出公式(5)的左邊，從而輕鬆構建整個公式(5)。

　　在論文的最後一部分，陶哲軒還討論了強猜想（1）的一些近似反例，這些例子表明，如果不假設一些“相當強的假設”，可能很難接近證明此猜想。

　　論文地址： 

　　https://arxiv.org/abs/2309.02325

　　參考鏈接：

　　[1]https://mathstodon.xyz/@tao/111018835694062000

　　[2]https://terrytao.wordpress.com/2023/09/06/monotone-non-decreasing-sequences-of-the-euler-totient-function/