只有懂流體靜力學,才配吃這塊月餅_風聞
中科院物理所-中科院物理所官方账号-09-29 13:16
月下一壺酒,桂花香濃,月影綽綽。
吳剛伐桂,玉兔搗藥。
此時的你,是否在歸家途中?
是否吃上了今年的第一塊月餅?
不論如何,
請收下我們為你準備的特殊驚喜:

1
特殊禮物的靈感
Mid-Autumn Festival
終於,每年一次可以敞開吃月餅不擔心長膘的日子。
我開始蒐羅各種月餅。
我曾經以為,香菜月餅已經是奇葩月餅界的天花板,直到我突然發現了…
臭豆腐辣條月餅,螺螄粉月餅,火鍋底料月餅….




月餅裏面真有螺螄粉、辣條、火鍋底料
於是,思路就此打開。
我靈機一動,給你們準備了剛剛的紅包,它有着響亮的名字:
“不懂流體靜力學都不配吃的月餅”
為什麼月餅會和流體靜力學扯上關係?
其實呢,這源於我突然而來的疑問:
為什麼月餅不是方的三角的,偏偏是圓的??
當我問我媽媽這個問題時,我媽媽説,蘇軾寫過一首詩,名字就叫《月餅》:
小餅如嚼月,中有酥和飴。
默品其滋味,相思淚沾巾。
既然是嚼着八月十五的月亮,那肯定是圓的嘛!
然而,我發現這其實是後人改編的,蘇軾寫的原版是這樣的:

《留別廉守》
宋·蘇軾
編萑以苴豬,墐塗以塗之。小餅如嚼月,中有酥與飴。懸知合浦人,長誦東坡詩。
好在真一酒,為我醉宗資。
這首詩其實並不是在中秋節創作的,寫的也只是蘇軾在喝酒,吃烤乳豬和小酥餅。
雖然但是,不愧是北宋資深美食家,蘇東坡!
事實上,中秋節賞月吃月餅的傳統,在明代的《西湖遊覽志會》中有描述:“八月十五日謂之中秋,民間以月餅相遺,取團圓之義”。
也就是説,月餅之所以是圓的,是藴含着團團圓圓的美好心願。
就像今晚,我們仰望星空,注視着那輪明月,許下美好心願。

緊接着,我的問題又來了:
為什麼月亮不能每天都是圓的,讓我們每天都團團圓圓呢?(小聲:還可以每天放中秋節)
2
月有陰晴圓缺
我們都知道,月球其實本身並不發光,我們看到的,只是它反射的太陽光。
由於月球繞着地球公轉,地球繞着太陽公轉,所以三者的相對位置一直在變化。月球被太陽照亮的那一面有時朝向地球,有時背向地球,結合下面的示意圖,就很容易理解:
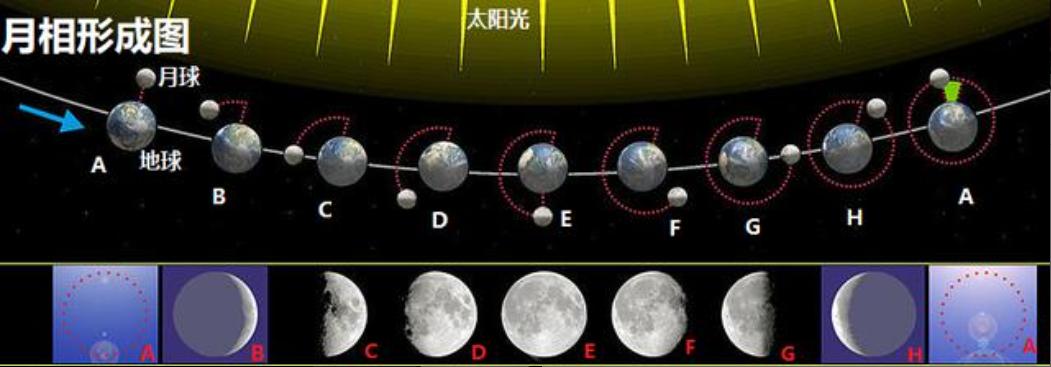
月相形成的簡單示意圖
例如,在A點,月球位於地球和太陽之間,月球被太陽照亮的那一面正好完全背對着地球,月球反射的太陽光無法傳播到地球上,所以我們就完全看不到月亮,這就是“朔”,也就是農曆初一。
相對的,在E點,太陽和月球分別在地球的兩邊,但三者一般不在同一個平面,所以地球並不會遮擋住太陽光,月球反射的太陽光被我們完全接收到,於是,就看到了一輪懸在夜空中的明月。
在我們的農曆中,每一天的月相,都有屬於自己的名稱,“新月”、“峨眉月”、“上弦月”、“滿月”….
我們的萬端情思,也都和月,相顧相憐。

“雲中誰寄錦書來,雁字回時,月滿西樓。”
“三更月。中庭恰照梨花雪。”
“桂花浮玉,正月滿天街,夜涼如洗。”
曾經照着古人的月光,如今灑在自己的肩頭,這難道不是一種超越了相對論的浪漫嗎?
接下來,我一邊賞月,一邊思考了下一個問題:
為什麼月球不是立方體?
如果月球是立方體,那我們看到的滿月就是方形,那現在市面上的月餅,不就都是方的了?
3
流體靜力平衡
事實上,太陽系中沒有任何一個天體是理想球體,赤道附近都有不同程度的隆起,就像是籃球上坐着個人那樣。
儘管如此,對於月球、地球、太陽這些大質量天體而言,至少都是類球體,而不是奇形怪狀的多面體,這是流體靜力平衡的結果。
終於,到了可以簡單推導公式的環節了!
在流體力學中,當流體靜止,或者每一點的流速不隨時間改變時,流體被認為處於靜力平衡狀態,此時該流體所受的合力為零。
我們可以用最簡單的模型來感受一下:
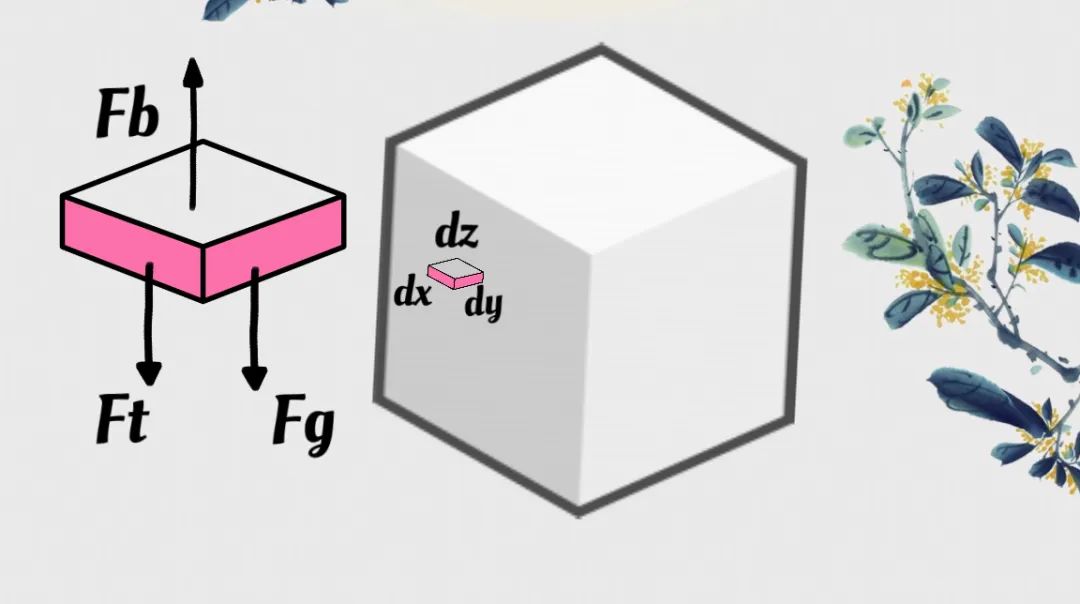
簡單示意圖
假設你將一個長方體的魚缸裝滿某種液體,在高度z處取一個微元長方體分析,長寬高分別是dx,dy,dz:
對於這個流體微元,它一共受到三種力:上方液體對它產生的向下的壓力Ft,下方液體對它產生的向上的推力Fb,以及向下的重力Fg。
假設這個微元長方體的上下表面所受的壓強分別是Pt和Pb,液體密度為ρ,重力加速度為g,規定向下為正方向,則可以得到下面的方程:
Ft=Pt·dx·dy
Fb=-Pb·dx·dy
Fg=ρ·dx·dy·dz·g
由於合力為零,所以上面三種力相加為零:
(Pt-Pb+ρ·g·dz)·dx·dy=0
也就得到了:
Pt-Pb+ρ·g·dz=0
假設這個微元的上下壓強差很小,密度ρ與壓強P相關,重力加速度g與高度z相關,則:
dP=-ρ(P)g(z)dz
考慮更簡單的情況:密度和重力加速度都是常數,積分後就可以得到下面這個式子:
P=-γz+C, γ=ρg
這就得到了流體靜力學的基本方程:
z+P/γ=常數
可以看出,這個方程描述的其實就是壓強在空間上的分佈規律。
如下圖所示,假設自由液麪的壓強是P0,高度是z0 ,液麪下方A處壓強是P,高度是z,根據上述公式可以得到:
z0+P0/γ=z+P/γ
z0-z=(P-P0)/γ
P-P0=γh=ρgh
P=P0+ρgh
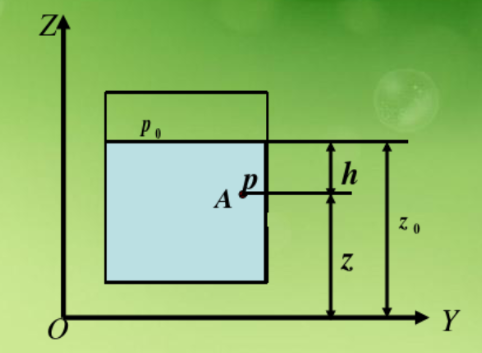
簡單示意圖
根據最終得到的公式,可以看出:在重力作用下的靜止液體,靜壓強隨着深度的增大而增大。任意一點的靜壓強P都是由兩部分組成的,即自由液麪壓P0+該點到自由液麪的單位面積的液柱重量ρgh。
對於同一種靜止液體而言,P0是常數,也就得到另一個推論:同一深度的各點靜壓強相等。
現在,讓我們再來重新看一下開頭的那道題:
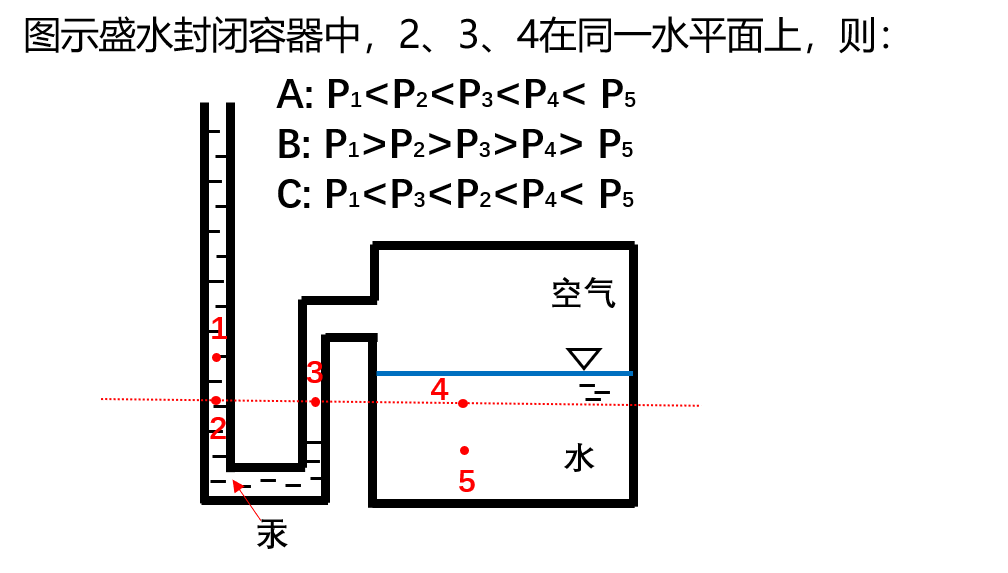
我覺得,你肯定知道正確答案了!
恭喜你,流體靜力學成功入門!
4
為什麼月球是球體
推導完公式,我們來放鬆一下:
還記得小時候玩過的橡皮泥嗎?
如果你收縮掌心,揉一團橡皮泥,儘量保證施加的壓力在各個方向上大小相等,最終橡皮泥會是什麼形狀?

大概率,應該接近球形。
當我們不再侷限於地球,放眼整個宇宙,也是類似的。
直白來講,天體在形成時,要麼是氣態的,要麼是熔融的,質量在不斷增加,產生的引力也隨之增加,當整個天體超過一定的質量後,引力就會變得非常強大,其中的原子就通過這樣強大的引力場相互吸引,最終不斷地向內壓縮成最緊湊的形狀:球體。
彷彿冥冥之中,有一隻巨型手掌在揉橡皮泥,最終揉捏出了這一個個的天體。
如今我們所觀察到的大質量天體,受到由內而外的熱輻射壓力和由外向內的引力作用,大小相等,方向相反,達到了一種流體靜力平衡態,各點的壓強分佈可以用上面類似的方法推出來。
如果我們去觀看宇航員在太空站喝水的視頻,可以發現,在微重力的太空中,液態水都會自發形成一個個小水球,這背後的原理,也是流體靜力平衡。

事實上,國際天文學聯合會對行星和矮行星的一個定義特徵就是:它們是具有足夠的重力來克服自身剛性並保持流體靜力平衡的物體。
如果是小行星帶裏的天體,因為質量太小,產生的引力不足以克服剛性力把天體壓縮成球體,所以基本都是不規則形狀--如果讓你用掌心,把一個鐵塊揉成一個鐵球,你一定也感到力不從心。
但,引力並不是全部。
天體還在不停地自轉,旋轉得越快,它的赤道凸起就越厲害,最終形成一個扁圓球體。
例如,木星是太陽系八大行星中自轉速度最快的,用小型望遠鏡就可以直接看出它明顯隆起的赤道。

朱諾號拍攝的木星照片
5
月餅與宇宙
以上,就是我的心路歷程。
如果進一步探討,甚至可以追溯到宇宙的起源。
宇宙也許曾經一片混沌,又燙又稠密。
但最後,形成了地球,有了月餅。
這裏面的奇妙,無法用言語形容。
但我相信,你已經懂了。
無需多言。
中秋月圓夜,唯伏乞三願:
一願故友安泰,
二願所思常健,
三願清輝拂照處,歲歲有佳宴。