本科生假期打零工,竟推翻了這個著名數學猜想_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!11-06 09:32

撰文 | 嘉偉
渴望假期是人類的共性,和教育背景、所學專業等無關。科羅拉多大學博爾德分校數學系研一學生Summer Haag,還有與她同系的Clyde Kertzer,早在今年5月就開始憧憬着這個暑假。Kertzer還在上本科,他計劃在暑假裏好好踢上幾場足球,然後精心準備自己的研究生入讀申請。Haag則期盼着在假期裏放鬆一下身心,重新拾起自己最熱愛的登山運動。
但是,當他們聽説自己的導師、數論專家Katherine Stange發佈了一個半日制暑期研究計劃之後,經過一番內心糾結,最終數學研究的熱情還是壓過了對於休假的渴望,他們兩人選擇申請加入其中。
Stange對“看似簡單但結構豐富的問題”很感興趣。她的團隊這一次所瞄準的數學對象,是數學史上最古老的幾何結構之一。Stange常見的研究風格則是,通過計算機生成大型數據集來解決數論裏難以捉摸的開放問題。作為項目組裏最年輕的兩位成員,Haag和Kertzer主要負責相對簡單的“體力勞動”——擴展組內數學家James Rickards的算法和初始代碼,編寫程序,生成大量模擬數據,最終以可視化的形式展示當數學結構進一步趨於複雜時的數值發展趨勢。
出乎所有人的意料,Haag和Kertzer加入項目組還未滿一個月,他們的勞動成果就打了整個數論領域一個措手不及。大量數據暗示,Stange團隊原本打算證明的那個猜想,實際上是錯的。在此之前,該領域的學者幾乎都相信它是正確的,唯一的問題在於如何證明它。
這個猜想發軔於最古老的尺規作圖問題,在文藝復興時期經由笛卡爾的美妙定理初見端倪,中間又有諾貝爾化學獎得主提供的洞察力,現在則跨進了最前沿的數論領域……它的來龍去脈,就如同一條經緯,貫穿了一部微縮的數學史。而始發站,正是兩千多年前的古希臘。
古希臘:阿波羅尼奧斯的相切圓
2200年前出生於小亞細亞佩爾加(今屬土耳其)的阿波羅尼奧斯(Apollonius of Perga)是歐幾里得之後,古希臘幾何學的第二位集大成者。由他所撰寫的8卷《圓錐曲線論》(Conics)是數學史上真正的經典鉅著,代表了希臘幾何的最高成就。

不過,我們下面要談到的是他的另一部作品《論相切》(On contacts或Tangencies)。
儘管原本的《論相切》已失傳,但通過後來幾代數學家的引用和註釋,我們仍然能夠了解一些其中的內容。其中最為重要的記錄來自大約500年後的《數學彙編》(Synagoge)一書,它由被譽為亞歷山大學派“最後一位偉大的幾何學學者”的帕普斯(Pappus)整理完成。

阿波羅尼奧斯在《論相切》裏提出了一個幾何學難題:在平面上給出位置關係沒有特別限制的三個圓,問如何用尺規作出第四個圓與之前的三個圓相切?此即著名的阿波羅尼奧斯問題(Apollonius’ problem)。
阿波羅尼奧斯找到了作圖方法,指出對於最一般的情況,一共有8個可能的解。
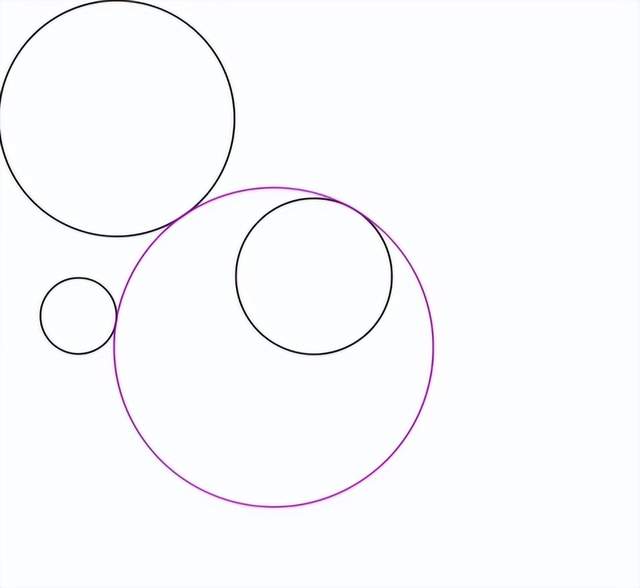
顯而易見,對於位置相對特殊的三圓配置,可與其全部相切的第四個圓,很可能不足8種。例如,若限定三個圓兩兩相切,則第四個圓僅有2種可能性。
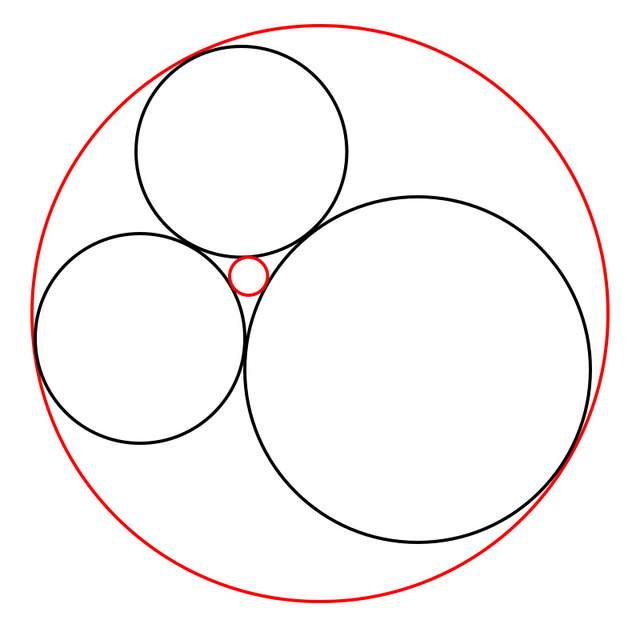
如果我們選擇包住三個小圓的大圓,則可以繼續用尺規作圖實現如下的操作:在大圓內部作出一個圓,使其與平面上已經存在(作出)的三個圓相切。顯然該過程可以無限持續下去,用越來越小的圓,填充圓與圓之間的空隙。效果如下圖:
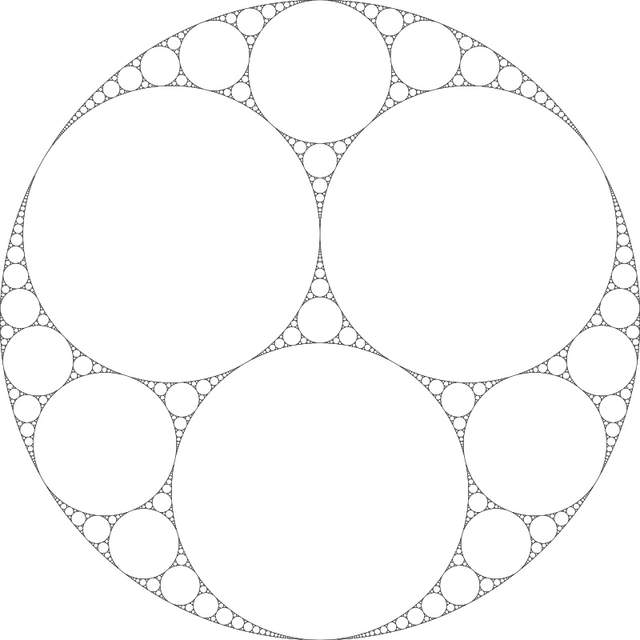
由於這些大大小小的圓盤就像是一個個密封墊,上圖裏的幾何結構被命名為阿波羅尼奧斯墊圓(Apollonian gasket)。這便是本文的“主角”。
在解決問題的過程中,阿波羅尼奧斯似乎使用了一個看似顯而易見的結論:在切點不重合的情況下,平面上至多隻能作出四個圓,使其任意兩個圓均相切;或者説,無論如何調節半徑大小和位置,都不存在五個圓,其中每個圓與另外四個圓相切。
但按照現代數學的公理化體系,“不存在五個圓,其中每個圓與另外四個圓相切”這一命題是可以證明,且應該予以證明的。此處便把它留作一個思考題。
文藝復興:笛卡爾的美妙定理
直到文藝復興時期,後世的數學家都企圖利用帕普斯對《論相切》的概述,重現阿波羅尼奧斯的原始發現。然而,真正繼承了阿波羅尼奧斯精神的是勒內·笛卡爾(René Descartes)。他引入了笛卡爾座標系,通過在平面上引入座標軸,將點與實數對應起來,從而將幾何問題轉化為代數問題。這一開創性的思想為後來的數學發展鋪平了道路。
更妙的是,具體到阿波羅尼奧斯問題——彷彿是為了昭示其繼往開來者的身份——恰也是笛卡爾本人,做出了阿波羅尼奧斯之後最為重要的發現:堪稱“美輪美奐”的笛卡爾定理。
為了介紹這個美麗的定理,我們不可避免地要涉及到曲率的概念。曲率,簡而言之,是描述曲線在不同位置上的彎曲程度的度量。
首先,想象一條直線。它沒有彎曲,因此其曲率為零。接下來,考慮一個圓,不管圓上的哪個位置,它的彎曲程度都是一樣的。圓的曲率似乎是一個常數。但是,當我們觀察拋物線時,情況就變得更加有趣。拋物線的曲率在不同位置上是不同的,因為其彎曲程度不均勻。
我們還可以通過一種直觀的物理圖像來理解曲率:想象一個小車沿着曲線運動。當小車轉彎時,它需要向中心點施加一個力,我們稱之為向心力。這個向心力的大小取決於小車的速度和轉彎時畫出的圓弧半徑。當轉彎半徑很小時,向心力會增大,這意味着曲線在該點的彎曲程度更高。
基於上述物理圖像,我們可以如此定義曲率:對曲線上的某一點A,該點的曲率是與曲線相切於A點的最大的圓的半徑的倒數。
需要注意的是,曲率定義中的相切圓必須是“最大的圓”。顯而易見,曲率越大,曲線的彎曲程度越高。對於一個圓,其圓周上各點的曲率都是自身半徑的倒數;對於直線,與之相切的圓的半徑,想要多大就可以有多大,所以直線的曲率是無窮大的倒數,亦即為0。
有了曲率的概念,我們就可以表述笛卡爾在研究相切圓時的發現。這位大哲學家斷言,只要四個圓彼此相切(切點不重合),則它們的曲率必然滿足如下簡單關係,
所有曲率的平方和等於曲率和的平方的一半。
如果四個彼此相切的圓的曲率分別為a、b、c、d,則上面的定理可用代數式表示成,2(a2+b2+c2+d2)=(a+b+c+d)2
笛卡爾定理的發現是數學上的一個里程碑,它代表了代數與幾何的融合,以及代數工具在解決幾何難題中的巧妙運用。從另一個角度來説,解析幾何之父率先找到了相切圓的幾何結構中的美妙代數關係,似乎也就順理成章了。
此外,還需要兩點額外的説明。
第一,在使用笛卡爾定理的時候,出於一些原因我們需要人為定義曲率的正負符號。若一個圓與另三個圓外切,則每個圓的曲率都是正數。但如下圖裏的大圓包含三個內切圓,則我們定義大圓的曲率為負數。如此一來,四個彼此相切的圓的曲率分別為a、b、c、d,如果a、b、c為已知,d的取值恰有正負兩種情況。
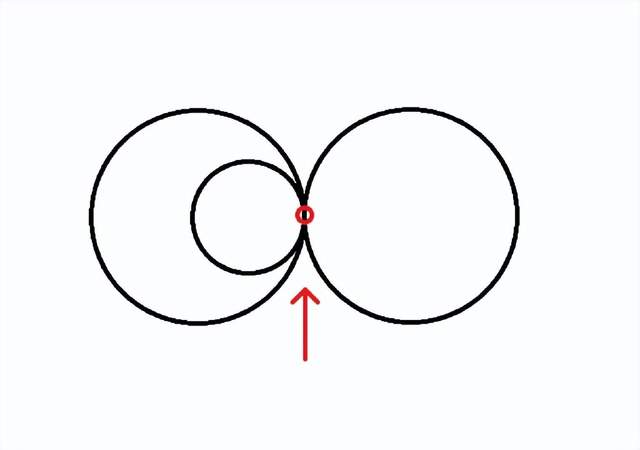
第二,在上一節裏我們提到過這個命題,“在切點不重合的情況下,平面上至多隻能作出四個圓,使其任意兩個圓均相切”。表述裏“切點不重合”的這個條件是必要的,如下圖,如果幾個圓切於一點,則上一節的命題不成立,笛卡爾定理也不成立。
20世紀:諾貝爾化學獎得主的數學讚美詩
英國化學家弗雷德裏克·索迪(Frederick Soddy FRS)在放射化學和原子物理學方面作出了重要貢獻。他與歐內斯特·盧瑟福(Ernest Rutherford)共同解釋了元素嬗變導致放射性的機制。他還證明了某些放射性元素同位素的存在性。1921 年,他被授予了諾貝爾化學獎,“以表彰他對放射性物質化學知識的貢獻”。
索迪對數學也非常感興趣,尤其是與圓或球相關的問題。
1936年,他獨立發現了上一節裏的笛卡爾定理。在進一步研究如何填充阿波羅尼奧斯圓的過程裏,索迪立刻注意到一個在過去200多年裏被數學家們所忽略的現象:當圓變得越來越小,曲率變得越來越大時,他期望得到一些帶有平方根或無限小數的複雜數字。然而,如果最開始的三個相切圓的曲率是整數,則後來所有圓的曲率都是整數。這是笛卡爾定理一個相當直接的結果,但幾百年來竟無人注意到。
激動之餘,索迪詩興大發,直接向《自然》(Nature)雜誌上投稿了一首數學詩。他用詩歌的語言描述了笛卡爾定理的內容。
詩的標題是The Kiss Precise(精確的吻,意指相切),摘錄若干翻譯如下:
要讓兩對嘴唇相吻也許/不需要任何三角學。
但當四圓相吻時/每個都要同時吻另三個夥伴。
四個圓的曲率之和/等於它們的平方和的一半。
如果你想知道它們的大小/只需解出我的方程。
……
雖然它們向歐幾里得保守住了秘密/現卻無需以經驗為據。
零曲率即變為直線/凹曲率應帶有負號的標誌,
待我再説一遍,所有四個曲率的平方之和/為其總和的平方的一半。
……
不過無論如何,索迪不僅展示了他對數學之美和詩歌藝術的熱愛,也為後來的研究提供了一個重要的工具。
如果説,笛卡爾的定理,從古老的歐式幾何學問題裏,信手拈出了其最核心的代數關係;索迪的“撿漏”發現則指出,這種關係藴藏了豐富的算術性質。
算術,即是數論。
啓蒙與理性時代:高斯的鐘表計數器與二次互反律
數論是基礎數學裏最古老但又很年輕的一個分支。
説它古老,早在歐幾里得的《幾何原本》裏便收錄並用反證法證明了最古老的數論命題:存在無限多個素數。
另外, 古希臘的丟番圖(Diophantus)留下了一篇具有數學謎題性質的《丟番圖墓誌銘》,後者因此被譽為最著名的不定方程(指未知數只能使用整數的整係數多項式方程)。也正是因為這一淵源,不定方程也被稱之為丟番圖方程。
説數論年輕,則是因為在隨後兩千年的數學史裏,雖然出現了費馬、歐拉、勒讓德(Adrien-Marie Legendre)等一大批推動了數論發展的巨人,但真正使這一數學分支嚴謹化和系統化的人,則是被譽為數學王子的卡爾·弗里德里希·高斯(Carl Friedrich Gauss)。
在高斯的《算術研究》第一章,他引入同餘的概念。他是第一位把算術裏最基礎的語言,同時也是藴藏着最深刻思想的工具——模運算——明確地“捻”出來的數學家。
為了方便後文的理解,這裏簡要介紹一下模運算。
在整數里,最基礎的關係是整除性。對於整數m和n。如果存在另一個整數k,使m=k×n,則我們説n整除m。如2整除4,7整除56等等。

遺憾的是,二次互反律的內容相對複雜,不適合在本文中進行介紹。
現代:本科生的工作推翻了前沿數學裏的著名猜想
掌握了模運算,也意味着我們終於來到了本次數學之旅的終點。
自從英國化學家索迪提供了頗具詩意的洞察——只要最開始的三個相切的圓的曲率是整數,則後來所有圓的曲率都是整數——數論學者就開始研究古老的幾何構造的算術性質。
考慮笛卡爾定理的表達式:2(a^2+b^2+c^2+d^2)=(a+b+c+d)^2,如果已知的三個數都是整數,則它顯然變成了一個丟番圖方程。
例如,現在有三個曲率分別為11、14和15的圓,你可以將這些數字代入由笛卡爾定理給出的方程,計算出能夠填充進它們之間的圓的曲率:86。
數論專家非常有興趣瞭解這個丟番圖方程的解的信息。譬如説,連續在大圓裏填充阿波羅尼奧斯墊圓,隨着圓的半徑越來越小,其曲率越來越大,相鄰的四個圓之間,又被笛卡爾定理約束;此時曲率的整數值會呈現出什麼樣的規律?
2010年,Elena Fuchs,現在是加州大學戴維斯分校(University of California, Davis)的一位數論專家,證明了曲率遵循一種特定的關係。
如果把每個曲率的數值mod 24,則會出現一條規則。有些構造只有與0、1、4、9、12或16同餘的曲率。其他一些僅留下餘數為3、6、7、10、15、18、19或22的曲率。
不久之後,藉助實際構造的有限模型,數學家們開始相信,如果某個阿波羅尼奧斯墊圓結構裏存在一組曲率,其中曲率的數值彼此互素,且每一個都與一個已知的整數r同餘 (mod 24),則除去有限的例外,這組曲率應包含了所有滿足下述同餘式的整數x:

回到本文的開頭,科羅拉多大學博爾德分校數學系研一學生Summer Haag與大四的Clyde Kertzer捨棄假期,加入了自家導師的暑假研究項目。他們的導師Katherine Stange希望能夠證明阿波羅尼奧斯墊圓上的局部—全局猜想。
她指派Haag和Kertzer編寫程序,生成大量阿波羅尼奧斯墊圓,以找出數據中隱藏的規律。Haag用Python腳本製作了一些同時繪製大量模擬圖表的程序。當Stange臨時離開學校,前往歐洲參加一場學術會議的時候,Haag做了一個大動作。
Haag一直在繪製1000個整數是如何相互作用——數據比它聽起來的要龐大,因為它涉及到100萬對可能的數字。然後她把參數調到了10000乘10000。在生成的圖表中,行和列裏的黑點拒絕消失。它看起來一點也不像局部-全局猜想的預言結果。
等Stange從歐洲返回,在每週的碰頭會上,Haag和Kertzer向項目組裏的成員展示了帶有反常數據的圖表。他們兩人承認,不知道是哪裏出了bug。
他們的導師凝視着圖表,突然説到:“如果是局部-全局猜想壓根就不成立呢?”
“我當時很興奮。很少有事情真正能讓我們感到驚訝。”Stange後來説,“但這就是數據的魔力。”
一旦找準了方向,Stange的團隊在幾周內就得到了一篇嚴格證明,否定了他們原本打算證明的猜想。

憑藉經驗、審美、乃至哲學主張,很多數學家養成了一種直覺,哪怕不知道如何證明一個猜想,他們也往往能夠以較大的勝率,猜測出猜想正確與否。比如説,對於國人熟知的哥德巴赫猜想(任一大於2的偶數都可寫成兩個質數之和),當代幾乎所有的數學家都相信它是正確的,雖然至今沒有人知道如何證明它。
幾乎所有的數論專家都曾以為,阿波羅尼奧斯墊圓上的局部—全局猜想是真的。不但有很多類似的已知結論支持他們的信念,同時對於這些行家裏手來説,他們看不出有什麼約束條件,會導致猜想不成立。結果這一次信念崩坍了。
原來,這些圓的曲率在滿足笛卡爾定理的時候,會以一種意想不到的方式受制於二次互反律(上一節提到的概念)。
Fuchs説:“沒有大量數據模擬,很難想象(他們)能憑運氣直接發現這個。”
“這純粹是巧合。”Haag承認。“如果我沒有把數據做得足夠龐大,我們就不會注意到它。”
這項工作對數論的未來,是一個好兆頭。很多數論學者開始自我反省。例如,在連分數領域裏有一個Zaremba猜想,之前大量數學家都相信它也是真的。但在局部—全局猜想被證否之後,人們開始下調自己的信心。“你可以通過直覺、通過證明來獲得數學上的經驗感悟。”Stange指出,“而且你非常相信它,因為你花了很多時間思考。但你不能和數據爭論。”
到此,阿波羅尼奧斯墊圓的故事,可以畫上一個臨時性的句點。或許,它遠不及費馬大定理的證明那樣恢弘、深邃,但關於這些相切的圓,它們擁有不輸任何數學分支的深厚歷史,它們具備簡單但十分精妙的代數特徵,以及目前僅僅揭開冰山一角的極其深刻的算術特性。
在前面提及“如果把每個曲率的數值mod 24,則會出現一條規則”時,不知大家有沒有感覺到這個數字24的出現,十分突兀。
其實這個24已經表明我們進入了某片數學深水區。這個數字在理論前沿分支中隨處可見,以驚人的方式將不同學科聯繫在一起。
由於一系列剛剛開始被理解的“巧合”,數字12和24在數學中發揮着核心作用。這一事實的第一個暗示是歐拉的奇異“證明”:
1 + 2 + 3 + 4 + … = -1/12。
上面的歐拉等式現在可以用黎曼zeta函數來賦予嚴格的數學意義,並且在物理學中它解釋了為什麼玻色弦理論在26=24+2維中效果最好。
同時,1^1+2^2+3^2+…+24^2=70^2,這一事實在弦理論、Leech晶格(是24維空間裏最密集的球體堆積方式,又是24!)和Monster羣之間建立了一種奇怪的聯繫。一個更為人所知的、密切相關的事實是“模形式”理論中的12-週期現象。數學家正在盡最大努力揭開深奧的謎團。
阿波羅尼奧斯墊圓本身,實際上對應於作用於某雙曲空間上的某個羣(“阿波羅羣”)的軌道。事實上,阿波羅羣是洛倫茲羣的一個離散子羣,在狹義相對論中非常著名!研究旋量的物理學家對它並不陌生!不過,最困難的還是本文所記述的,關於數論方面的問題。它是非常罕見的,把數學源頭——古希臘的幾何,與現代最前沿的數學領域之一——自守形式,聯繫在一起的數學對象。
參考資料
[1].Two Students Unravel a Widely Believed Math Conjecture | Quanta Magazine
[2].THELOCAL-GLOBALCONJECTUREFORAPOLLONIANCIRCLEPACKINGSIS FALSE,2307.02749.pdf (arxiv.org)
[3].《通俗數學名著譯叢-奇妙而有趣的幾何》,戴維·韋爾斯著,於應龍譯,上海教育出版社
[4].ONTHELOCAL-GLOBALCONJECTUREFOR INTEGRALAPOLLONIANGASKET,1205.4416.pdf (arxiv.org)
[5].阿波羅尼奧斯(古希臘數學家)_百度百科 (baidu.com)
[6].Descartes’ theorem - Wikipedia
[7].《一線串通的初等數學》,張景中著,科學出版社
[8].Apollony fractal (paulbourke.net)
[9].Soddy’s hexlet - Wikipedia
[10].Hexlet -- from Wolfram MathWorld
[11].Apollonian circle packings: number theory - ScienceDirect
[12].丟番圖 - 維基百科,自由的百科全書 (wikipedia.org)
[13].模算數 - 維基百科,自由的百科全書 (wikipedia.org)
[14].Apollonian gasket - Wikipedia
[15].John Carlos Baez: “Here’s an ‘Apollonian gasket’.…” - Mathstodon
[16].faculty.math.illinois.edu
[17].My Favorite Numbers (ucr.edu)
本文受科普中國·星空計劃項目扶持
出品:中國科協科普部
監製:中國科學技術出版社有限公司、北京中科星河文化傳媒有限公司

1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權説明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。