速度疊加的一個簡單常識_風聞
平常-无尽世界。12-15 18:51
【本文來自《一個難倒全世界科學家和學者的小學數學題》評論區,標題為小編添加】
- guan_15685916721577
- 本文是根據狹義相對論的推導分析的。其圖示和公式都是取自狹義相對論的光線走過的路程為:rAB+v(tB-tA)= c(tB-tA)。本文是認為這個公式推導難倒了我們科學家和學者。所以根據狹義相對論的推導圖示才有了上面的解法。
速度疊加的一個簡單常識。
比方説,船的速度是v=5米/秒,一個人在船上奔跑,速度是u’=4m/s;那麼,在地面參照系來看,這個人的速度就是u=4+5=9米/秒。我們可以根據經典物理的伽利略變換去推導速度疊加公式。由於x=x’+v*t,方程兩邊對時間t求導數,就是dx/dt=dx’/dt+v, dx/dt的物理意義就是物體的速度u,即u=u’+v。
倘若船的速度非常快,是光速的一半,即v=c/2,而奔跑速度也非常快是u’=c/2,那麼,在地面參照系看,這個人的速度就是u=c/2+c/2=c嗎?當然不是。答案是0.8c,這需要相對論修正。
相對論的洛倫茲變換x=γ(x’+v*t’), t=γ(t’+v*x’/c^2)。我們寫成微分形式,dx=γ(dx’+v*dt’), dt=γ(dt’+v*dx’/c^2)。兩式相除,令u=dx/dt,u’=dx’/dt’,那麼就得到相對論速度變換公式,u=(u’+v)/(1+u’*v/c^2),這個分母中多的一項u’*v/c^2就是相對論修正因子。顯然,如果物體的速度u’或者參照系的運動速度v很小(與光速c相比),那麼這個修正因子就約等於0,這就近似為伽利略速度變換,簡單的速度疊加。
如果u’及v都很大,比如c/2的量級,那麼相對論效應就顯著了。我們代入看看,u=(c/2+c/2)/(1+c/2*c/2/c^2)=c*4/5。
如果u’=0.9c和v=0.9c,那麼物體的速度u=1.8c/1.81=0.9945c。如果u’=c和v=c,那麼u=2c/(1+1)=c,這就是光速最大。物體的運動速度u最快也不超過光速c。
速度的相對性。如果v=0.9c,u’=-0.9c,那麼u=(-0.9c+0.9c)/(1-0.81)=0。就是説,在實驗室參照系看,我們是相對地面靜止的,而高能粒子的運動速度是+0.9c,向前近光速運動;但若在高能粒子的視角下,它自己是靜止的,而我們的速度是-0.9c,向後高速運動。
如果v=0.9c,u’= -0.9c-1m/s;那麼u≈(-0.9c-1m/s+0.9c)/(1-0.81)= -5.26m/s。就是説,我們的速度(向後)從0增加到5m/s;但在高能粒子看來,只是增加了1m/s。
再看一下光速不變原理。 如果u’=c, 那麼u=c。 u=(c+v)/(1+c*v/c^2)=c。 就是説,以高速v運動的高鐵列車上發出的光,在地面看的光速仍然是c。不是人們一般想當然的以為的c+v,會超過光速。
若運動參照系的速度v是光速c,那麼裏面的任何物體的速度,在地面參照系來看,都將是光速c。 我們把v=c代入,u=(u’+c)/(1+u’*c/c^2)=c。在相對論的理論框架下,超光速是不可能的,無法想象的。
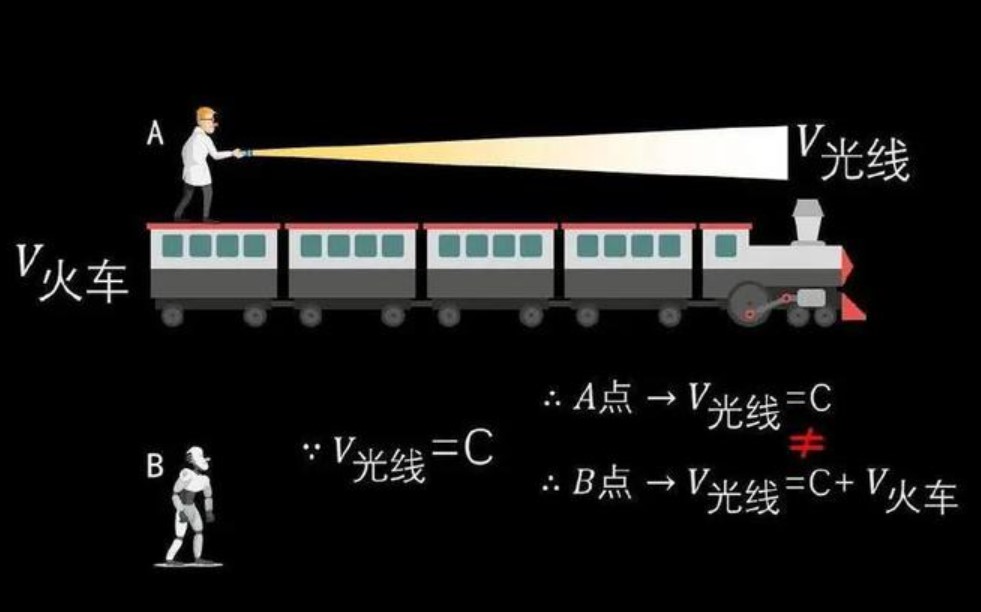
當然,這一切建立在光速不變,光速為什麼不能與其他速度疊加的公理之上,公理就不需要理由,不需要證明。人類現在通過各種方式觀測到光速就是不變的,當然會做出“光速不變”這個結論,更何況麥克斯韋電磁理論中,光速的確是一個常數。
