AI 首次攻克難倒陶哲軒數學難題:DeepMind 里程碑算法登上 Nature_風聞
镜子里的陌生人-人来人往谁还在?潮起潮落我自观12-15 20:28
困擾數學家多年、讓陶哲軒直呼喜歡的上限集問題數學難題,竟然被 DeepMind 的新算法破解了?這是史上首個用 LLM 發現的算法,堪稱里程碑級研究,一經發布立馬登 Nature。
上限集問題,是困擾數學家們多年的開放性問題。
著名數學家陶哲軒,就曾將上限集問題描述為自己最喜歡的開放性問題。
陶哲軒博客
而大語言模型,竟然在這個問題上做出了新發現。
今天,Google DeepMind、威斯康星大學麥迪遜分校和里昂大學的研究人員聯手提出全新方法 ——FunSearch,竟首次利用 LLM 發現數學科學中的開放問題!
AI 通過搜索計算機代碼編寫的「函數」,因此得名 FunSearch。

論文地址:https://www.nature.com/ articles / s41586-023-06924-6
簡單來説,FunSearch 將預訓練的 LLM 與自動「評估器」配對使用。前者的目標是以計算機代碼的形式提供創造性的解決方案,後者則防止幻覺和錯誤的想法。
通過在這兩個組件之間來回迭代,初始解決方案「進化」為新知識。
DeepMind 為了讓所有人見證這一歷史性時刻,先把未編輯的版本發了出來。

Nature 新聞稿更是直言:DeepMind 的 AI 在未解難題上勝過了人類數學家!

這是人類首次使用 LLM 挑戰科學或數學中的開放性問題,並做出了新發現。
另外,為了證明 FunSearch 的實用性,DeepMind 專家還嘗試用它解決「裝箱問題」,這個問題應用範圍很廣,可以提高數據中心的效率。
而對於這個問題,FunSearh 同樣發現了更有效的算法。
DeepMind 專家表示,科學進步非常依賴分析新知識的能力,而 FunSearch 之所以成為強大的科學工具,就是因為它輸出的程序不僅提出瞭解決方案,還揭示瞭解決方案是如何構建的。
這樣,使用 FunSearch 的科學家就能進一步被啓發出新的想法,進入「改進-發現」的良性循環。
LLM 通過「進化」推動科學發現
大模型最擅長解決問題,但可以發現全新的知識嗎?
由於 LLM 無法避免「幻覺」輸出事實不正確的信息,因此依靠它們獲得事實上正確的新發現非常困難。
但是,如果我們能識別和擴展 LLM 最好的創意,將其創造力發揮到極致如何?
FunSearch 利用大模型的力量,通過一種「進化」的方法發展和保留最優秀的創意想法。
這些想法用計算機代碼表達出來,可以自動運行和評分。
首先,用户以代碼的形式對問題進行描述。此描述包括一個用於評估程序的過程,以及一個用於初始化程序池的種子程序。
FunSearch 是一種迭代程序,每次迭代時,系統都會從當前程序池中選擇一些程序,並將其輸入 LLM。
LLM 在此基礎上創造性地生成新程序,並自動對其進行評估。
評分最高的程序會被添加回現有程序池中,形成一個自我改進的循環。
值得一提的是,FunSearch 使用的是谷歌的 PaLM 2,但它也兼容其他經過代碼訓練的 LLM。
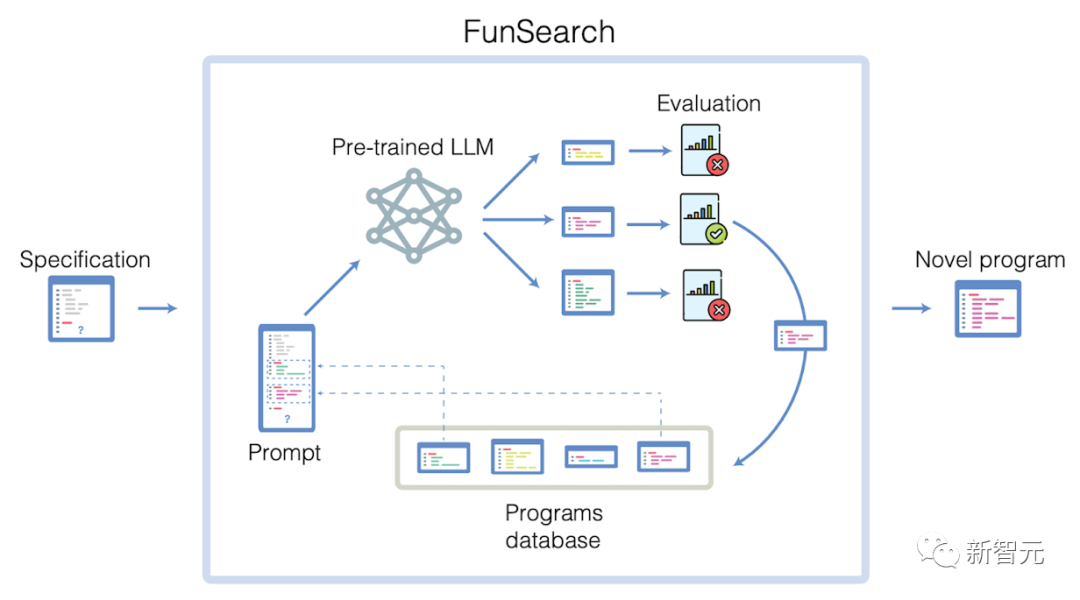
FunSearch 整體流程示意圖:向 LLM 展示它迄今為止生成的最佳程序(從程序數據庫中檢索),並要求生成一個更好的程序。LLM 提出的程序會被自動執行和評估。最好的程序會被添加到數據庫中,供後續循環選擇。用户可以隨時檢索迄今為止得分最高的程序。
在不同領域發現新的數學知識和算法,是一項眾所周知的艱鉅任務。很大程度上,這遠遠超出了最先進的 AI 系統的能力範圍。
為了利用 FunSearch 解決此類難題,DeepMind 研究人員引入了多個關鍵組件。
並非從 0 開始,而是從有關問題的常識開始「進化」過程,讓 FunSearch 專注於尋找最關鍵的想法,以實現新的發現。
此外,進化過程還使用一種策略來提高想法的多樣性,以避免停滯不前。最後,DeepMind 團隊並行運行進化過程,進而提高了 LLM 的效率。
開天闢地的數學發現
上限集問題是一個開放性挑戰,幾十年來一直困擾着多個研究領域的數學家。
這一次,DeepMind 研究者與威斯康星大學麥迪遜分校的數學教授 Jordan Ellenberg 合作,Ellenberg 教授在上限集問題上取得了重要突破。

論文地址:https://arxiv.org/ abs / 1605.09223
上限集問題的關鍵之一,就是在高維網絡中查找最大的點集(即上限集),在這個點集中,任何三個點都不能位於同一條線上。
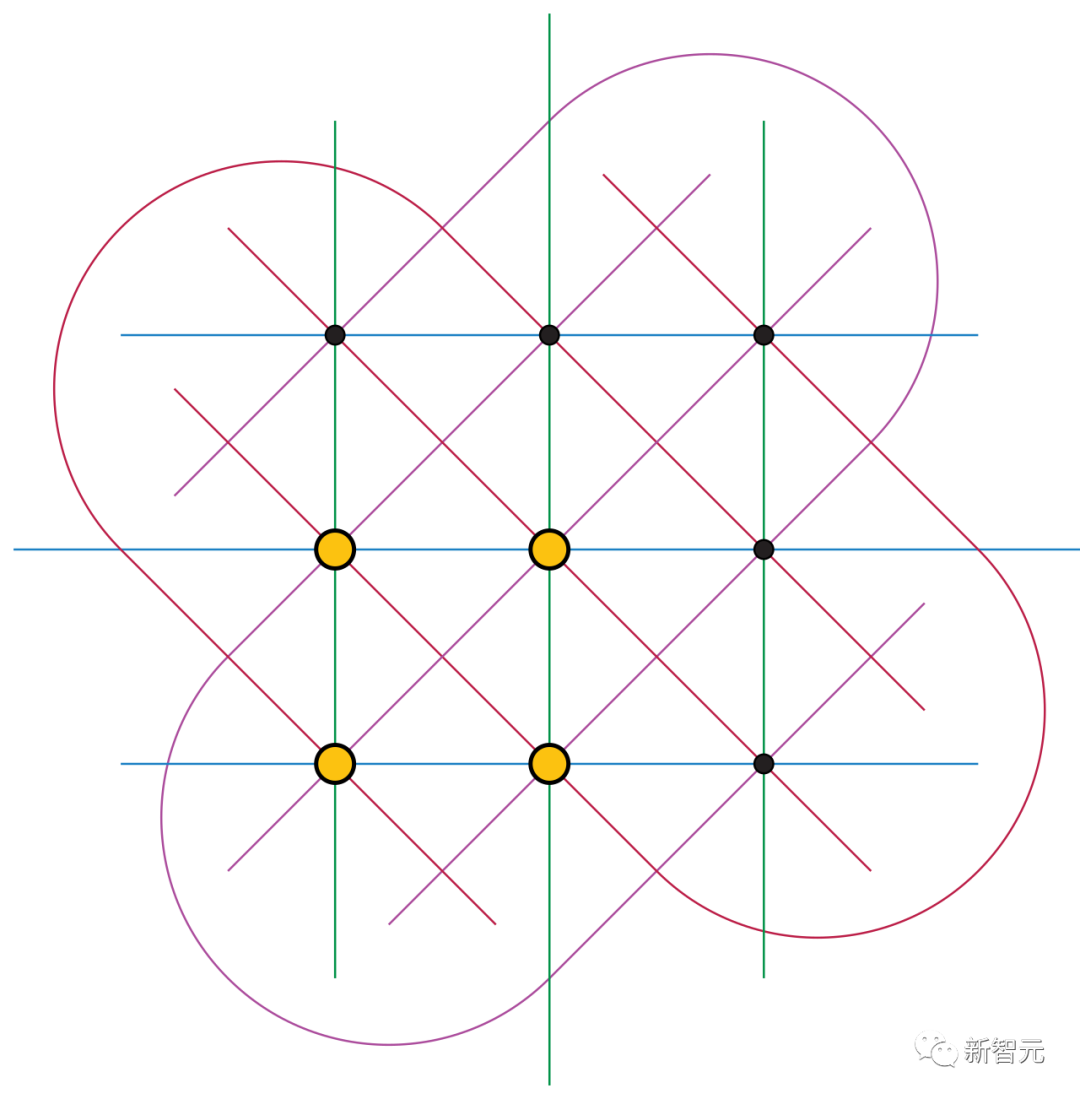
上限集問題之所以如此重要,就是因為它可以作為極端組合學中其他問題的模型,這些問題會研究數字、圖形或其他對象的集合最大能有多大,最小能有多小。
然而,要解決上限集問題,靠蠻力的計算方法肯定是行不通的,因為要考慮的可能性實在太多了,很快就會超過宇宙中的原子數量。

陶哲軒對於上限集問題為何重要的解釋
對此,FunSearch 通過程序的形式生成了解決方案,在某些設定中,發現了有史以來最大的上限集。
這個發現,代表了過去 20 年中上限規模的最大增幅!

而且,FunSearch 的表現也優於最先進的計算求解器,因為這個問題的擴展遠遠超出計算求解器目前的能力。

下面這張交互式圖,展示的就是從頂部的種子程序到底部的更高評分新函數的演變。
其中,每個圓圈都是一個程序,其大小與分配給它的分數成正比。右側是 FunSearch 為每個節點生成的對應函數。(函數的完整程序,可以參考原論文)

交互體驗鏈接:https://storage.googleapis.com/ deepmind-media / DeepMind.com/ Blog / funsearch / index.html

以上結果表明,FunSearch 技術有能力突破複雜組合問題的既定研究成果。而在這類問題中,建立直觀理解通常非常困難。
研究人員表示,非常期待這種方法能夠在組合學的其他類似理論問題中為新發現出力,甚至在未來為傳播理論領域開闢新的可能性。
FunSearch 打開「黑盒」,與數學家合作成典範
FunSearch 偏愛簡潔,且人工可解釋的程序。
雖然發現新的數學知識本身就很重要,但與傳統的計算機搜索技術相比,FunSearch 方法還具有額外的優勢。
這是因為,FunSearch 並不是一個僅僅生成問題解決方案的「黑匣子」。
相反,它會生成描述「這些解決方案是如何實現」的程序。
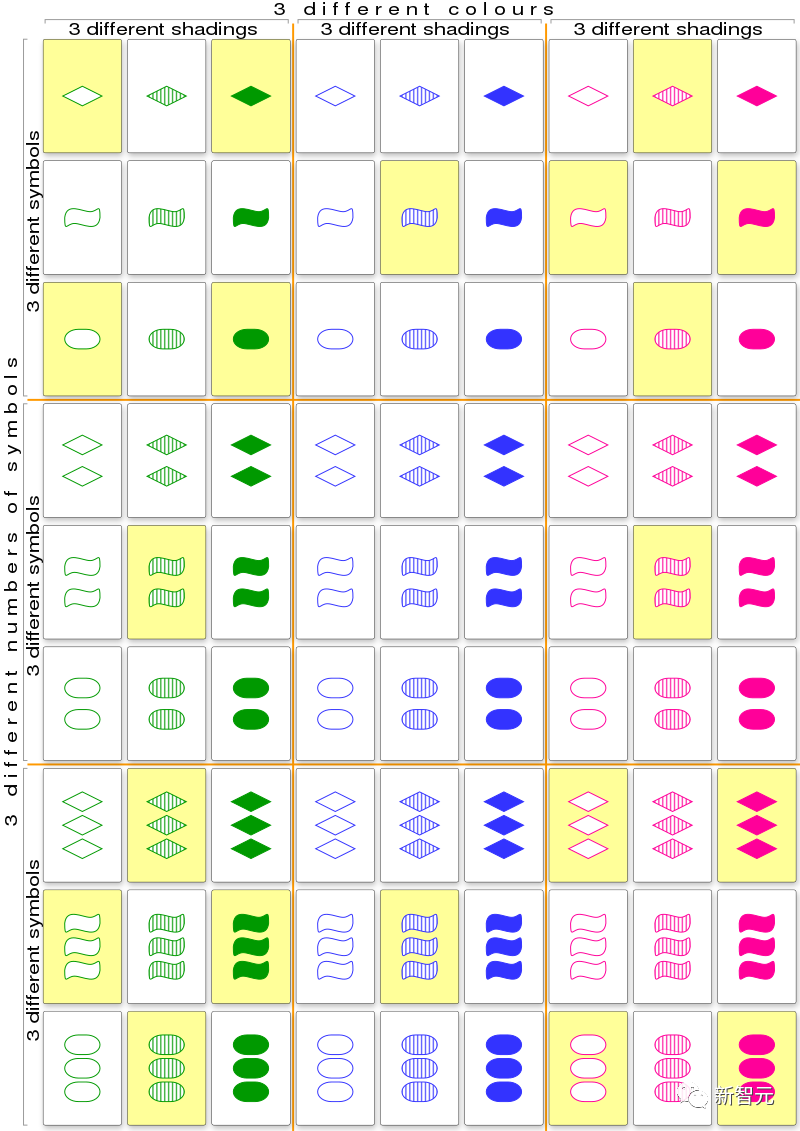
這種「展示工作過程」(show-your-working)的方法,類似於科學家的工作方式,可以更好地解釋和復現新發現的過程。
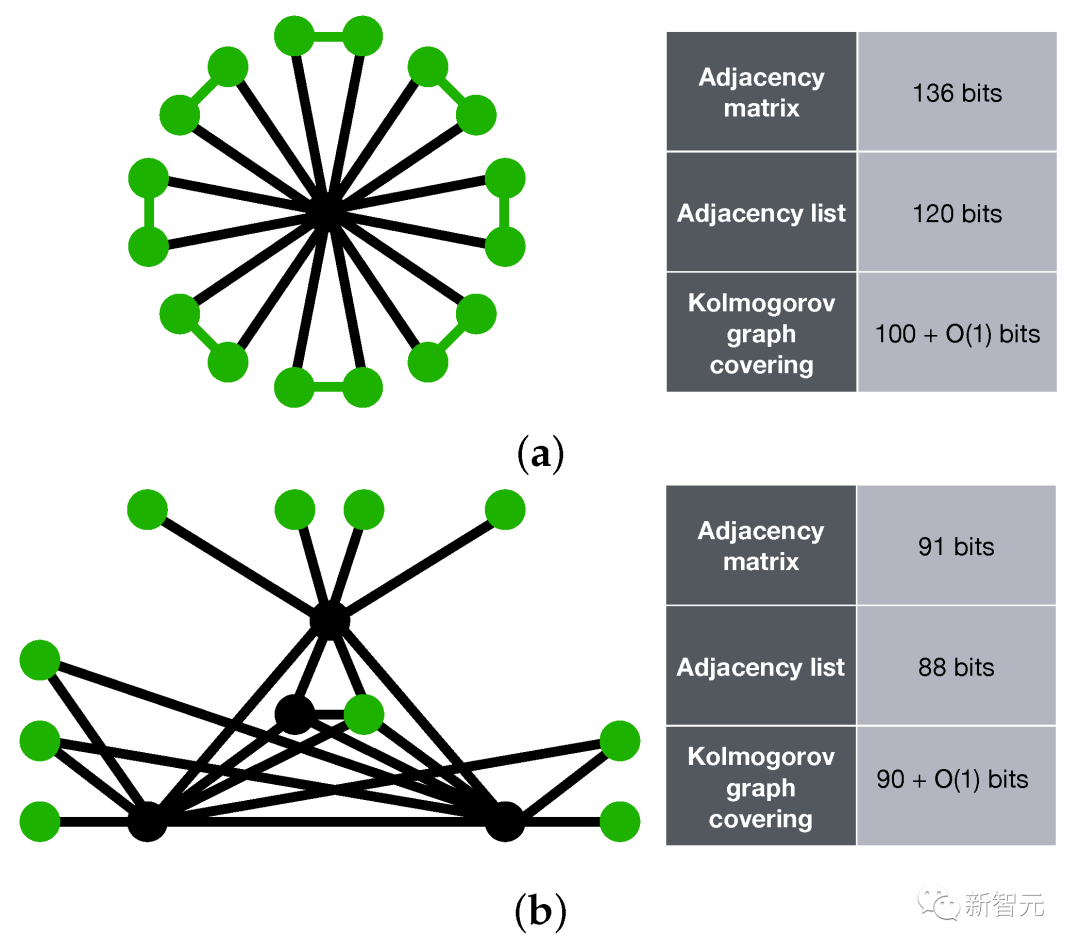
FunSearch 傾向於由「高度緊湊的程序」表示的解決方案 —— 具有低柯爾莫哥洛夫複雜性(Kolmogorov complexity)的解決方案。

簡短的程序可以描述非常大的對象,從而使 FunSearch 能夠擴展到海量數據中尋找小目標的問題。
此外,這也讓研究人員更容易理解 FunSearch 的程序輸出。

美國數學家 UW-Madison 教授,論文盒著者 Jordan S. Ellenberg 稱,「FunSearch 為制定攻擊策略提供了一種全新的機制。FunSearch 生成的解決方案在概念上要比單純的數字列表豐富得多。當我研究它們時,我學到了一些東西」。
更重要的是,FunSearch 程序的這種可解釋性,可以為研究人員提供可操作的見解。
比如,當使用 FunSearch 時,它的一些高分輸出的代碼中,存在耐人尋味的對稱性。
這讓研究人員對問題有了新的瞭解,並利用這種見解來完善 FunSearch 中引入的問題,從而得出更好的解決方案。
DeepMind 認為,「這是人類和 FunSearch 之間在許多數學問題上進行協作的典範」。

左:通過檢查 FunSearch 生成的代碼,研究人員獲得了更多可操作的見解(標亮)。右:使用左側更短的程序構建的原始「可接受」集合。解決計算機領域「裝箱問題」重大挑戰
既然能夠在理論上限集問題上取得成功,DeepMind 研究人員嘗試探索 FunSearch 在計算機科學領域的靈活性。
應用在計算機科學中一個重要的實際挑戰,來探索全新方法的靈活性。
這裏,採用了一個具有挑戰性的「裝箱問題」(bin packing),即將不同大小的物品打包到最小數量的箱子或容器之中。
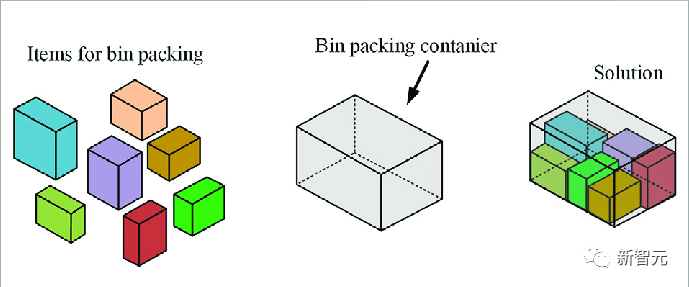
這一問題是解決許多實際問題的核心,從物品裝入集裝箱,到在數據中心分配計算作業,以最大限度地降低成本。
在線裝箱問題,通常是使用基於人類經驗的算法經驗法則(啓發式)來解決的。
但是,為每種不同規模、時間或容量的特定情況找到一組規則,就可能有挑戰性。
儘管與上限集問題有很大不同,但為這個問題設置 FunSearch 卻很容易。
FunSearch 提供了一個自動定製的程序來適應數據的具體情況,性能要優於以往的啓發式方法 —— 使用更少的箱子來包裝相同數量的物品。

現有啓發式算法:最佳適應啓發式算法(左)和 FunSearch 啓發式算法(右)「裝箱問題」的示例。
在線裝箱這類困難組合問題,也可以使用其他 AI 方法來解決,比如神經網絡和強化學習。這些方法都被證明是有效的,但是要部署它們,很可能需要大量資源。
而 FunSearch 輸出的代碼,卻可以輕鬆地檢查和部署,這就意味着:這種解決方案可以應用於現實世界的工業系統中,快速帶來好處。
LLM 驅動的科學及其他領域的發現
FunSearch 的設計表明可以防止 LLM 產生「幻覺」。
這些模型的力量不僅可以助力數學領域的新發現,還可以找到解決實際問題的最佳解。
DeepMind 認為,對於科學和工業中的許多問題,其中無論是長期存在的還是新的問題,使用 LLM 驅動的方法來生成有效且定製的算法,將會是常見的實踐。

事實上,FunSearch 開創性工作僅僅是個開始。
隨着 LLM 的能力範圍進一步擴展,FunSearch 也會自然得到改進。
與此同時,DeepMind 還將努力擴展其能力,以應對各種社會迫切需要解決的的科學和工程挑戰。
網友熱議
如果所有的幻覺都是準確的,全新的見解將加速基礎科學的發現。

還有人表示 AGI 的門檻就是做出新的發現,那麼我猜我們現在已經有 AGI 了。

2007 年,世界上最偉大的數學家陶哲軒稱「上限集問題」是他最喜歡的開放性問題。現在,谷歌的 DeepMind 的 FunSearch 成功解決了這個問題。

「LLM 不能發現任何新東西,它們只是隨機的鸚鵡」。FunSearch 實際上可以在數學和計算機科學中發現新的有用的東西。
這句話明着點名 LeCun 本人。

那麼,P=NP 的證明何時實現?

參考資料:
https://deepmind.google/discover/blog/funsearch-making-new-discoveries-in-mathematical-sciences-using-large-language-models/