年末啦!當別人抽走三等獎,你抽中一等獎的概率會變大嗎?_風聞
中科院物理所-中科院物理所官方账号-01-29 16:57
原創:中科院物理所
當裏郎當
只聽見一陣音樂聲響起
實驗室裏空無一人
活動室裏熱鬧非凡
他們這是在幹什麼?
哦,原來是物理所的新春派對!

這種活動,自然是少不了小白的(雖然沒什麼才藝,但是作為觀眾,那絕對是説得過去的)。
小白之所以要來,除了節目很精彩以外,還有一個更重要的原因,抽獎!
引子
抽獎可是一個活動最誘人的部分,不僅獎品豐厚,而且也很考驗實力(魯迅説過,運氣是實力的一部分)。雖然小白一次大獎也沒中過,但是,這不妨礙他參加活動的熱情!
本次抽獎規則公佈如下:
獎池裏有一等獎3個,二等獎5個,三等獎若干,所有參與抽獎的人員最低可以獲得三等獎。四個遊戲幣可以抽獎一次,並且每個人只有一次抽獎機會。遊戲幣可以在遊戲區獲得。
雖然運氣從不光顧小白,但是他每次都忍不住要試一試。於是乎,他開始在遊戲區叱吒風雲。
可是,小白一個遊戲幣也沒得到的時候,已經有很多人在排隊抽獎了。
小白的心懸到了嗓子眼,萬一一等獎被抽完了怎麼辦?可是,他轉念一想,這些先抽獎的大概率抽中的都是三等獎,那麼每抽走一個三等獎,他抽到一等獎的概率就大一點。這麼一來,小白反而開始暗自慶幸了。
這個時候,另一位老白同學走了過來,告訴他,其實不管抽獎順序如何,只要抽獎的人沒有公佈自己抽到的結果,那麼每個人抽中一等獎的概率都是一樣的。
小白覺得很難理解,隨着獎池裏的三等獎減少,抽中一等獎的概率不就是越來越大嗎?仔細一想,他才反應過來,他之所以覺得自己抽中一等獎的概率在變大,是因為他知道抽獎箱裏三等獎減少了,如果每個抽獎者都公佈自己的結果,那麼每次都相當於****對獎池進行了一次重新分配,那他抽中一等獎的概率自然就變大了。
但是對於在一旁專注玩遊戲,沒有看到前面抽獎結果的人來説,他們抽中一等獎的概率是均等的,這才保證了抽獎的公平性。
為了讓小白更好地理解這個事情,老白給他講了很經典的“三門問題”
換,還是不換
三門問題最初來自於一個電視節目,大意是這樣的:
**會場上放着三扇門,其中一扇門後面放一輛汽車,另外兩扇門後面放的是山羊,參與者隨機打開一扇門,如果打開的這扇門後面是汽車,那麼他就可以獲得這個汽車。主持人知道哪扇門後面放的是汽車。**現在想象你就是這位參賽者,當你選中一扇門打開它之前,主持人決定再給你一次選擇的機會。主持人打開了一扇後面放着山羊的門,那麼,你要選擇另外一扇門嗎,還是堅持你的選擇?
當老白把這個故事講完的時候,小白陷入了沉思。
第一次選擇的時候,選中汽車的概率是1/3,當一扇後面放着山羊的門被打開之後,只剩下兩扇門,那麼換與不換,選中汽車的概率不都是1/2嗎?
但是老白告訴他,這樣是不對的。
事實上,如果不換的話,選中汽車的概率還是1/3,如果換的話,選中汽車的概率就會變為2/3。
怎麼會這樣呢?小白冥思苦想,也得不到答案。
看着小白眉頭緊鎖,額頭上不一會兒就湧現出豆大的汗珠,老白決定直接告訴他,事實上,我們可以把所有可能的結果列出來,這就是我們高中學過的枚舉。
當主持人打開一扇後面是羊的門之後,情況就變成了這樣子:
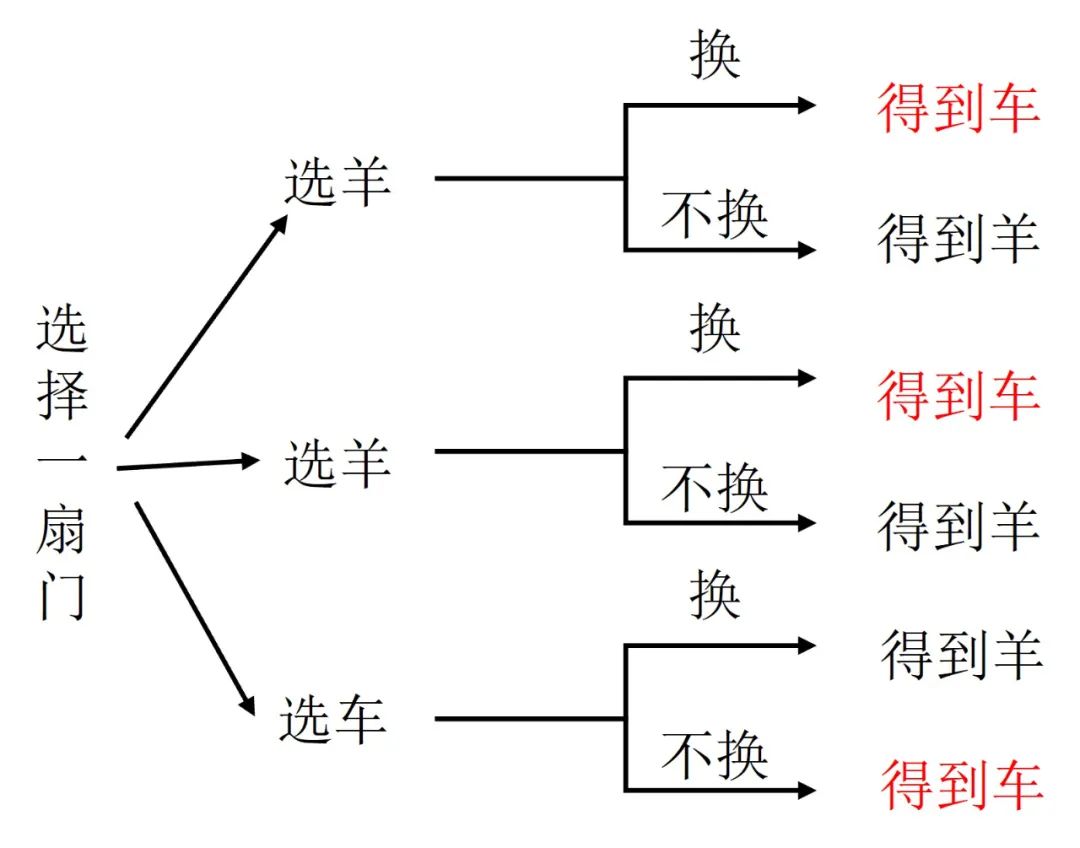
這樣一來,答案就一目瞭然了。
可是小白不理解為什麼會出現這樣的矛盾呢?
這時候不妨讓阿白出場。在主持人打開那扇後面放着羊的門之後,阿白來了。這時候如果讓阿白選一扇門,他選中汽車的概率是多少呢?毫無疑問,是1/2。
因為阿白沒有先驗條件,對於他來説,擺在他面前的只有兩扇門,其中一扇門後面放着一輛汽車,那他選中汽車的概率自然是1/2,可是對於小白來説,他已經做過一次選擇,因此他再次選擇的時候要在這個前提下考慮。
小白明白了,在遇到概率問題時,要考慮到已知的事實,在對的前提條件下分析才能得出正確的答案。
雖然經過一番分析,小白接受了換之後概率變大這個事實,但是他還是決定不換。萬一換了之後,門後面是山羊,那不是血虧。儘管概率變大了,可是並不能保證換完他一定能選中汽車,因此出於這種不讓自己後悔的考慮,他決定不換。
那麼如果是你,你會不會換呢?
擲硬幣
為了考察小白是否真的理解了這種反直覺的問題,老白又給他出了一題:
連續擲兩次硬幣,已知其中一次是正面朝上,那麼另外一次也是正面朝上的概率有多大?
小白不假思索地就要給出1/2的答案,可是轉念一想,老白既然這樣問了,那這道題肯定存在貓膩。於是小白利用剛才使用過的枚舉法,把所有情況都列了一遍:

沒錯,已知一次正面朝上的話,那另一次也正面朝上的概率就是1/2,於是他很開心地給出了答案,還附上了自己的分析。
可是老白聽後只是笑了笑,回答了兩個字:錯了。
小白一頭霧水,想不明白錯在了哪裏。
老白説,我把題目稍微改一下,你再來看:
連續擲兩次硬幣,已知第一次是正面朝上,那麼第二次也是正面朝上的概率有多大?
這個問題毫無疑問答案就是1/2,因為第一次的結果對第二次完全沒有影響,兩次擲硬幣是完全獨立的,那擲一次硬幣正面朝上的概率就是1/2。
那麼最初的問題答案為什麼不是1/2呢,仔細對比一下,小白髮現,在最初的問題中,題目中給的是**“其中一次是正面朝上”**,而沒有説是哪一次正面朝上,因此要考慮到順序問題,所以所有可能的結果就不是三種,而是四種:

那麼已知其中一次朝上的情況下,另一次也朝上的概率就變成了1/3.
生日悖論
經歷過兩次失敗後的小白沒有放棄,而是越戰越勇,於是他讓老白給他再出一道題,這次老白給他出了經典的“生日悖論”問題,題目是這樣的:
只考慮一年有365天的情況,一個課題組至少有多少名學生就可以使至少兩個學生同一天過生日的概率大於50%?
小白想了想,他發現這道題正向思維很難給出答案,因為“至少兩個學生同一天過生日”包含的情況太多,這時候他想起了高中概率題常用的辦法。
既然正向考慮很難把所有情況都列舉出來,那不妨來算一下所有人都不在同一天過生日的概率,只要“所有人都不在同一天過生日”的概率小於50%,那麼“至少兩個人同一天過生日”的概率就大於50%。
有了思路之後,小白就開始計算,這時他也顧不上排隊玩遊戲賺遊戲幣了,已經一門心思地沉浸在瞭解題的快樂中。
第一個人有365種選擇,第二個人和第一個人不在同一天過生日,他有364種選擇,第三個人和前兩個人都不在同一天過生日,他有363種選擇,以此類推,前n個人都不在同一天過生日的概率為:
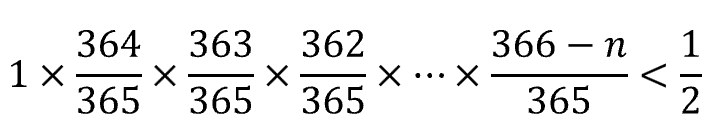
當n=23時,上述條件滿足。
算出這個結果後,小白大吃一驚,本來直覺告訴他應該是一個很大的數,沒想到只要23個人就可以使至少兩人同一天過生日的概率大於50%。
雖然很難理解,但數學應該是不會錯的。
就像薛定諤的貓一樣,小白就怎麼也理解不了,為什麼在觀測之前,貓處在又死又活的疊加態。在小白看來,貓的生死狀態是確定的,無論你觀測與否,這都應該是既定的事實。可能這就是量子力學的迷人之處吧,到處都透露着反直覺。因其難以理解而更加吸引人。
尾聲
經過幾次失敗,小白終於答對了一道題,對於這種違背直覺的概率問題也有了一些認識,所以他重拾信心,又回到遊戲區大展身手。
這個時候,工作人員宣佈,5個二等獎已經全部被抽走,3個一等獎還都在。這一下,小白一掃心中的陰霾,一下子輕鬆了許多,因為這樣一來,他能抽中一等獎的概率大了許多。
終於,小白集齊了四枚遊戲幣,來到抽獎區,在抽獎箱裏排山倒海地挑了一番,抽上來一個三等獎……
雖然今天晚上學會了很多概率題,但是概率畢竟只是一種可能性,即使抽中一等獎的概率是99%,那剩下1%的小概率事件依然有可能發生。
概率正因其不確定性而迷人,這也是抽獎的樂趣所在。因此無論中獎與否,概率都是一門有趣的學問。
新春派對結束了,物理所的研究生們帶着對科研的熱忱,重新回到了自己的崗位上。