龍年吃太飽 | 過情人節還是迎財神？大年初五的難題_風聞

原創：中科院物理所 

“大年初五財神至，喜祿春風進萬家”。俗以正月初五為財神生日，是中國民間迎財神的日子。而今年更為特殊，迎財神和情人節的日子撞上了。是為了祈求一年的好財運而舉辦迎財神活動，還是和心上人一起度過一個甜蜜的情人節呢？

在噼裏啪啦的歡騰裏，在年味正濃的新春時光中，個人情感問題總是備受關注，如果沒有對象的話，那麼選擇過情人節應該是個零概率事件，因為單身貴族們完全不需要糾結，已經歡天喜地迎財神了。接下來，我們站在第三方的視角，來思考廣大有對象的羣體會如何選擇。

過情人節和迎財神，兩種決策的概率

如何****分佈？

把問題模型簡化和具象化，選取樣本對象為：有對象的人。他們會選擇哪種方式來度過自己的大年初五呢，選擇過情人節或迎財神的人羣比例分別是多少呢？選擇過情人節的人羣中是有錢羣體的概率是多少呢？

假如你正處於一段甜蜜的戀愛中，你身邊的人也沉浸在成雙成對的幸福中，那麼你會不會覺得大多數有對象的人應該都會去過情人節吧？

但如果你現在飽受金錢的困擾，會不會覺得即使有對象也會選擇迎財神呢，能選擇過情人節的人應該大部分很有錢吧？

很明顯，這些答案都帶有強烈的個人色彩。心理學研究顯示，事物的可想象性、新近性、顯著性、生動性等因素會影響人的記憶和認知。

可被我們想象出來的、在我們身邊發生的以及反覆被強調的事更容易被從記憶庫中調出來，成為我們的認知依據。

那麼事實到底是怎樣呢？學過概率論的小夥伴們應該遇到過一個很經典的問題。如果有一種疾病發病率是0.1%，針對這種疾病測試（陽性或陰性）的準確率是99%。請問如果一個人測出了陽性，那麼他真的得病的概率是多少？

不要輕易相信直覺，特別是對於概率問題。

也許有人第一反應是得病的概率是99%。思維陷阱在於：一般而言，我們會**把陽性和得病綁定，因為陽性是得病的典型特徵****，**但是忽略了不得病的人羣基數其實是更大的。實際上真的得病的概率為：

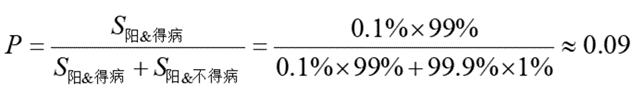
很明顯，這個概率遠低於我們的直覺。

也就是説，測出陽性後得病的真實概率除了考慮測試準確率"99%"，這個**“**代表性概率”，還應該考慮無條件概率，也就是在人羣中隨機挑選，極低的發病的概率。而我們往往會過於關注代表性特徵，而忽略了其他的重要信息，這就是我們常見的認知誤區——代表性偏差。

回到我們的正題，兩者類比，得病和不得病對應有錢(事件M)和缺錢(事件SM)，陽性和陰性對應過情人節(事件Y)和不過情人節（迎財神(事件N))。雖然有點扎心，但是有錢到不重視財運的人羣比例確實較少。

我們假定：有錢就是擺脱了金錢的束縛和誘惑，有錢羣體中幾乎所有人都選擇過情人節，概率為P(Y|M)，接近1；缺錢羣體中大部分人選擇迎財神，概率為P(N|SM)，大於0.5；有錢和缺錢羣體的人數比例按照經濟學的二八定律簡單估算一下為：2：8。

很明顯，過情人節還是迎財神的概率分佈，受到多種因素的影響，離不開經濟狀況和大家心中的價值排序。當經濟狀況改變時，有錢(事件M)和缺錢(事件SM)羣體的比例會改變，當錢和情的價值排序變化時，概率P(N|SM)和P(Y|M)也會動態變化。下圖為一種可能的概率分佈：

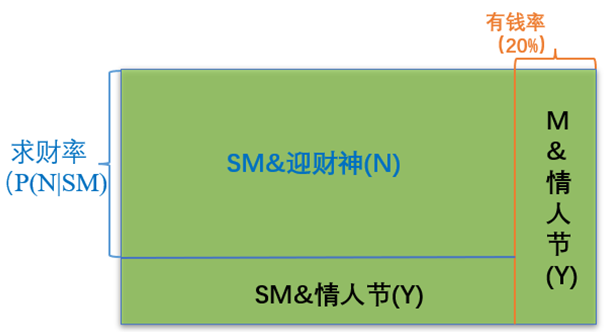
過情人節羣體中為有錢羣體的概率為：

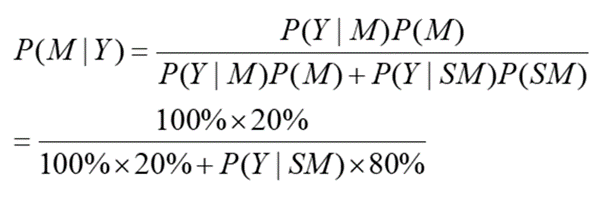
經過計算可知，當P(Y|SM) > 0.25時，P(M|Y) < 0.5，即當缺錢羣體中選擇過情人節的比例超過25%時，過情人節羣體中缺錢羣體的比例更高。

這種情況打破了我們一般的思維慣性，因為缺錢羣體的人數更多，所以過情人節中有錢者的概率有可能更小。

掀起概率的頭紗：貝葉斯派

上文真實概率的計算中使用的便是大名鼎鼎的貝葉斯公式：

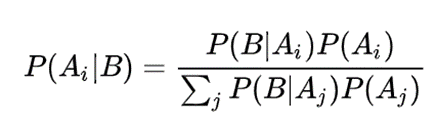
P(Ai)是事件Ai的先驗概率，之所以稱為"先驗"，是因為它不考慮任何其他方面的因素。但是如果事件Ai的發生受到事件B的影響，那麼其概率需要更新為條件概率P(Ai|B)，也被稱作Ai的後驗概率。

在統計學領域，存在着兩大主流學派——頻率學派和貝葉斯學派。歷史上，針對**“概率是什麼”等本質問題**，頻率學派和貝葉斯學派曾爭論不休，貝葉斯統計也曾受到主流數學家的排斥，但是如今貝葉斯概率已經成為一個熱門課題，在機器學習以及量子力學等重要領域都有應用。

圖源：網絡 

貝葉斯學派核心理念是觀察者可以通過不斷進行觀測或實驗獲得新證據來及時調整、更新對事件發生概率的認知。也就是不斷增加條件B來更新對事件A發生概率的認識。

而頻率學派的核心思想是基於大樣本理論，將概率定義為隨機事件多次發生的頻率的極限。當樣本數量足夠大時，頻率就逼近於客觀概率。

但有些時候我們無法獲得大量樣本，那麼我們也無法獲得真實的概率。對於小****樣本數據，貝葉斯學派便是解決這個問題的一把利器。

貝葉斯學派認為概率可以是一個動態的變量，概率被定義為對事件的信任程度，這是一種基於觀察者內部知識體系的主觀信念。例如，你認為飛機失事的概率取決於你對飛機失事發生的信心，如果你非常相信飛機這種交通工具，那麼你認為的概率就越小。當然，我們的最初想法（先驗）未必是準確的，所以我們需要新數據來更新我們的先驗概率。

拿最簡單的拋硬幣模型為例，我們設定這是一枚公平（即硬幣拋出正反面的概率相同）硬幣的先驗概率為P(A)=0.9（即信任度為90%）。接着，通過不斷地拋硬幣來獲得新的實驗數據，以此更新我們的先驗概率。

首先將硬幣拋擲拋一次，結果為硬幣是正面，將第一次實驗得到的數據結果命名為事件O，根據貝葉斯公式，可計算出：在事件O發生的條件下，硬幣是公平的條件概率為：

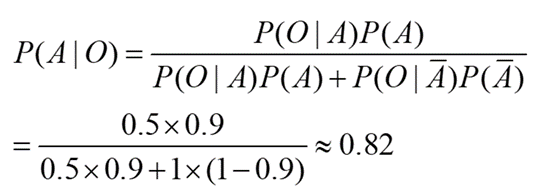
拋第二次，硬幣仍然是正面，先驗概率被更新為P(A | OO)，根據上述方法，計算得到概率P(A | OO) = 0.69;以此類推，P(A | OOO) = 0.53，P(A | OOOO) = 0.36，當連續四次拋出正面時，對這枚硬幣是公平的信任度急劇下降，這説明該硬幣很有可能是一枚不均勻的硬幣，或者是一枚兩面都是正面的硬幣。

貝葉斯學派便是利用這樣一種方式將先驗概率與樣本數據進行結合，得到後驗概率，並以此作為對未知量的推斷。

貝葉斯理論擴展了概率的涵義，概率可以是一種主觀置信度，是對一個事件的信任程度，讓主觀概率的概念走入人們的視野。

感受一下主觀概率

以三門問題為例：三扇關閉的門後面分別藏着汽車和兩隻羊，參賽者需要選中藏有汽車的門才能贏獎；如果參賽者先選定了一扇門但未打開，這時已知答案的主持人打開了剩下兩扇門中有羊的一扇，那麼請問參賽者要不要選擇另一扇門呢？

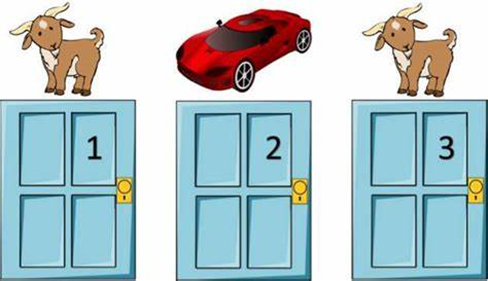
圖源：網絡

把這個問題拓展一下會很好理解，非常契合我們“敏鋭的第六感”。如果現在改為有十扇門（其實多多益善），你先任意選一扇，主持人在剩下的九扇門中一扇一扇的打開，打開了八次，門後出現的都是羊，那麼留下的最後一扇門中有汽車的概率是不是很大呢？你要不要換呢？

其實，最開始你的選擇便把抽中大獎的概率不均等的一分為二：分別是你選擇的那扇門佔據的1/10的概率，和主持人在剩下的九扇門中進行操作而重新分配的9/10的概率。主持人的操作便是在把中獎的幾率逐漸累加在最後未被打開的一扇門上，在這種情況下，如果你選擇換，那麼中獎的概率會有9/10，交換讓中獎率翻了9翻，當然要換。

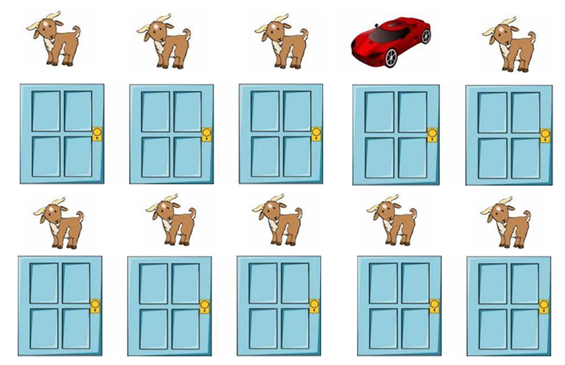
回到三門問題，主持人剩下的那一扇門其實承載着2/3的中獎概率，所以參賽者應該選擇交換。 

小編自己也曾很苦惱於三門問題，因為總是會陷入一個反駁的想法：不管遊戲規則是如何，到了最後一步，參賽者都是在兩扇門中二選一，那概率為什麼不是1/2呢？

但是當小編接觸到了在貝葉斯理論中可以得到有效應用的主觀概率，自恰了，雖然關於概率為1/2的反對想法會與最後的真實實驗結論相悖（相悖的原因是遊戲規則必須考慮），但是這種想法是有價值的，它就是小編的一種主觀概率觀。

非常有趣是：主觀概率是沒有標準答案的，我們每一個人都可以給某個事件賦予概率。不同的人對同一事件是否發生的信心是不同的，我們每天都在基於自己以往的經驗、獲取的信息，來做出判斷與選擇，基於你的實際情況，你賦予自己過情人節和迎財神這兩個事件的概率分別是多少呢？

最後，由衷地祝願大家情場春風得意，錢途璀璨長明！