當三個小夥子同時愛上一個姑娘，還得靠數學知識來解決問題？_風聞

原創：中科院物理所

 

龍年伊始，有三個小夥子，同時愛上了一個姑娘。

為了娶到這個姑娘，他們決定：

用手槍，進行一次決鬥。

阿武的命中率是30％，小胡的命中率是50％，而老郭是神槍手，他從不失誤，命中率是100％。

為了公平一些，姑娘讓他們按這樣的順序決鬥：

阿武先開槍，小胡第二，老郭最後。

然後不斷循環，直到，只剩下一個人。

那麼，這三個人中，誰最有可能活下來，娶到姑娘呢？

血戰到底

忽略這詭異的血戰到底的設定，不難發現，這是一道很有意思的概率推理題。

別急，我們慢慢來捋一捋思路：

首先，阿武作為第一個開槍的人，他肯定不會去打小胡，因為如果小胡不幸中彈身亡，接下來老郭就會開槍打自己，那自己必死無疑。

所以，阿武肯定會選擇先開槍打老郭。

其次，如果老郭能活到開槍的時候，並且這時候阿武和小胡都還沒死，那老郭肯定會選擇先把命中率更高的小胡打死；

所以，小胡肯定會希望老郭活不到開槍的時候，因此小胡也會選擇先打老郭。

確定這兩點以後，我們就可以開始分類討論了：

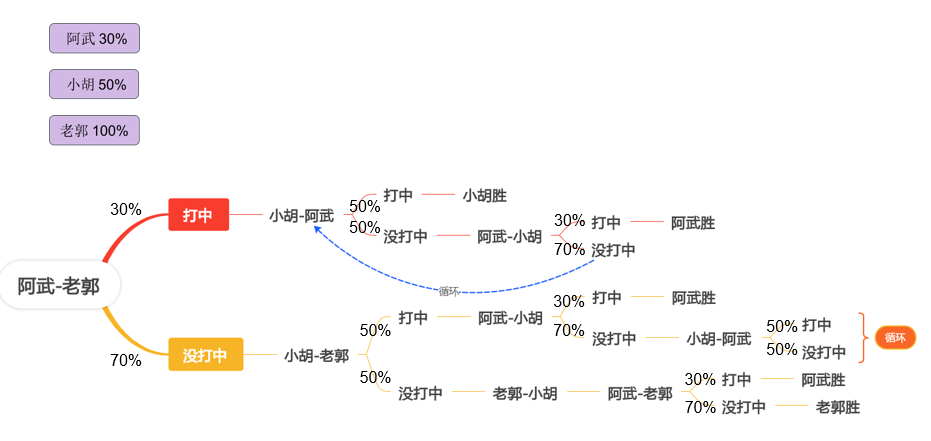
首先，我們來看看神槍手老郭獲勝的概率，根據上面的思維導圖，只有一種情況下，老郭能夠獲勝：

阿武和小胡都沒打中老郭，老郭先開槍命中了小胡，然後阿武又沒打中老郭，老郭又開槍命中了阿武，這樣，老郭的獲勝概率就是：

70%*50%*70%=24.5%

接下來，我們來看看阿武獲勝的概率：

①：阿武和小胡打老郭都沒打中，小胡被老郭打中，然後老郭被阿武打中，這時候阿武勝，概率是：70%*50%*30%=10.5%；

接下來的情況，最後都是只剩下阿武和小胡兩個人對決，由於他們都不是百發百中的神槍手，所以問題進入了不斷循環：

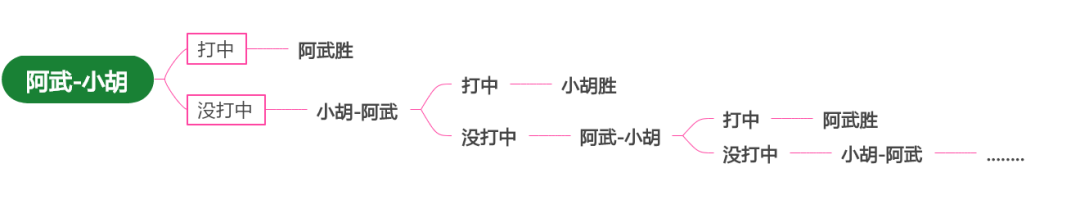
如果彼此都一直打不中對方，他們倆可以相互開槍，一直到地老天荒….

因此，如果單算只剩阿武和小胡兩個人後，阿武向小胡開槍，最後阿武獲勝的概率：

30%+70%*50%*30%+70%*50%*70%*50%*30%+….+

不難發現，這就是一個等比數列的求和，最後整個概率總和就是：

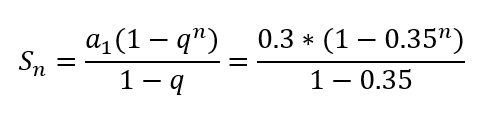
當n趨於無窮的時候，整個值的極限就是46.2%；

這時候，我們再考慮上前提條件，老郭提前出局，輪到阿武先向小胡開槍，一共有兩種情況：

①：阿武打中老郭，小胡沒打中阿武，最後阿武和小胡循環交戰，阿武勝的概率是：30%*50%*46.2%=6.9%

②：阿武沒打中老郭，小胡打中了老郭，然後又開始阿武和小胡的循環交戰，於是阿武勝的概率是：70%*50%*46.2%=16.2%

所以，阿武獲勝的總概率就是三種情況相加：

10.5%+6.9%+16.2%=33.6%

最後，我們來看看小胡獲勝的概率，理論上我們用100%減去阿武和老郭的獲勝概率，那就應該是小胡的獲勝概率，但萬一我們上面算錯了呢？

保險起見，我們還是來具體算一下，思路和阿武的類似，假設小胡先開槍打阿武，最後小胡勝：

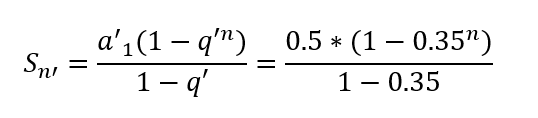
當n趨於無窮的時候，整個值的極限就是76.9%；

最後會變成小胡向阿武開槍，進入循環對戰的情況，一共也就兩種，概率相加就是：

30%*76.9%+70%*50%*70%*76.9%=41.9%

至此，我們總結一下：

阿武獲勝概率是33.6%;

小胡獲勝概率是41.9%；

老郭獲勝概率是24.5%。

三者相加概率是100%，也側面驗證了，小編應該沒有算錯？

所以，最有可能活到最後的，並不是神槍手，而是隻有50%命中率的小胡。

藍眼島問題

假設小胡真的活到了最後，如願娶到了心愛的姑娘。

他們來到一個島上，進行蜜月旅行。

這個島上住着100個人，其中有3個紅眼睛，97個藍眼睛。

對於這100個島民而言，有三個奇怪的規則約束着他們：

1：他們不能照鏡子，不知道自己眼睛的顏色。

2：他們不能告訴別人對方的眼睛是什麼顏色。

3：一旦有人確定了自己是紅眼睛，他就必須在當天夜裏自殺。

這天，小胡在和全島人一起狂歡的時候，不留神就説了一句話:你們這裏有紅眼睛的人。

問題來了:

假設這個島上的人足夠聰明，每個人都可以做出縝密的邏輯推理。請問，這個島上將會發生什麼?

這是一道很經典的邏輯推理題。

這種推理都不能泛泛而談，要從最特殊的視角出發，代入思考，才能最快得到答案。

我們不妨假設紅眼睛的三個人分別是A,B,C，那麼對於紅眼睛C而言，他看到了兩個紅眼人A和B，他就會這樣想：

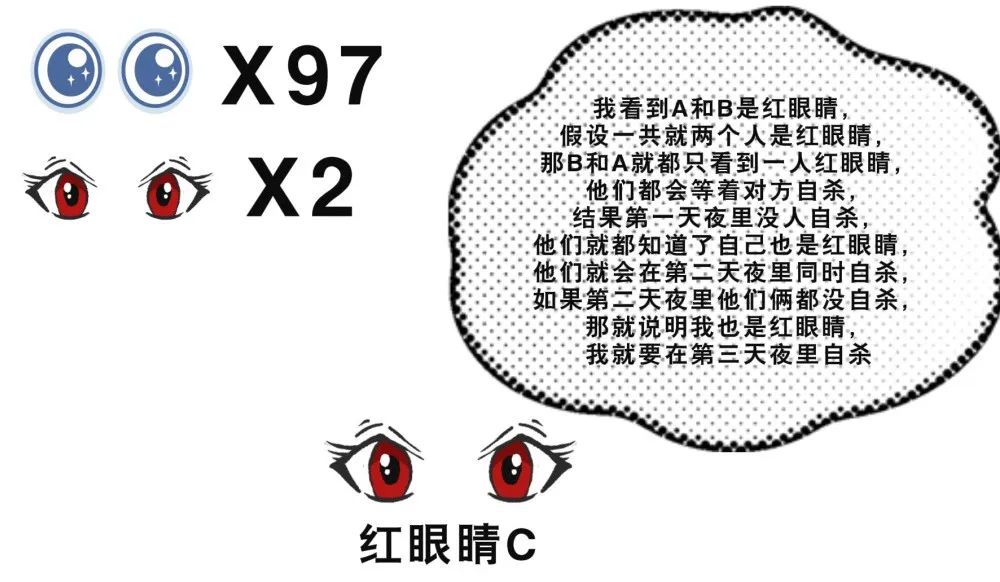
同樣的，紅眼人A在等着B和C第二天自殺，紅眼人B在等着A和C第二天自殺，結果第二天誰也沒自殺。

於是，根據他們縝密的推理邏輯，三個紅眼人都會在第三天確認自己也是紅眼睛，選擇在第三天夜裏同時自殺。

所以，正常情況下，故事的結果就是：

第三天夜裏，三個紅眼人同時自殺。

看上去，小胡説的這句話並沒有更多信息。

他沒説一共有多少個紅眼人，也沒説誰是紅眼睛，為什麼最後紅眼人就自殺了呢？

這就涉及到邏輯學中的共有知識和公共知識。

共有知識，是一個羣體的每個人都知道的事實，但是不知道其他人是否知道;

公共知識指一個羣體的每個人不僅知道這個事實，而且每個人都知道該羣體的其他人也知道這個事實，並且其他人也知道其他的每個人都知道這個事實…..

這麼説可能比較抽象，舉個不是很嚴謹的例子：

高中的時候，中午最後一節課一般到11點40。

有的時候老師會拖堂，大家都意識到老師拖堂了，但不知道其他同學有沒有注意到，不敢提醒老師，又擔心食堂沒飯吃。

這時候，有個同學提醒道：”老師，已經下課了。"

這下，大家心裏就都清楚了，原來其他人也意識到老師拖堂了。

老師拖堂這件事情，就從共有知識，變成了公共知識。

同樣的，在這裏，島民都知道島上有紅眼睛的人，但不知道其他人是否知道，這時候，“島上有紅眼睛的人”叫做共有知識。

當小胡把這句話喊出來後，這句話就變成了公共知識，所有人都知道了“島上有紅眼睛的人”，並且也知道了其他人也知道“島上有紅眼睛的人”。

所以，最後，那些紅眼睛的人，才會自殺。

這在現實生活中，其實很常見。

一支股票，大家覺得垃圾。有權威機構發文，認定這是垃圾股，大家跟帖討論也都覺得這是垃圾股，這就會變成公共知識，這支股票就會一路狂跌，沒人願意接盤。

你看了這篇推送，覺得邏輯學真有意思，認為這文章很不錯，然後你看到下面的評論也都在這樣説，於是，”這是篇優秀的科普文“就成了公共知識，小編就會很快樂！

小試牛刀

剛剛我們分析的這兩道題，其實都涉及了分類假設和概率計算。

毋庸置疑，在物理研究中，邏輯思維也是很重要的。

在研究晶體結構和性質的對應關係時，我們需要從晶格、軌道、電荷、自旋等多個角度分類解析；在生長出的材料性能不好時，我們需要從結果倒推可能的原因。甚至，我們從初中物理就開始用到的控制變量法，也藴含着很典型的邏輯思維。

所以，做一些有趣的邏輯思維題，並不是浪費時間，這能夠幫助我們靈活思維，尋找新的科研思路。所以，今天還是中科院物理所（邏輯所）！

這裏還有一道很經典的過橋問題（小學奧數題），大家可以在走親訪友嗑瓜子的時候，來思考一下：

春節了，小明一家要去河對岸拜年，需要過一座橋，過橋時是黑夜，所以必須拿着唯一的燈過橋。

已知，小明過橋要1秒，弟弟要3秒，爸爸要6秒，媽媽要8秒，爺爺要12秒。每次過橋最多可過兩人，而過橋的速度依過橋最慢者而定，而且燈在點燃後30秒就會熄滅，並且不能再點燃。

問：小明一家過橋，至少需要多長時間？

歡迎在評論區留下你的答案！

祝大家新年新氣象，邏輯推理一年更比一年強！