經典理論都與量子理論“糾纏”，為何熱力學是唯一例外？_風聞

近年來，伴隨着量子信息的迅速發展，測量糾纏熵已經不存在原則性的技術障礙。是否能夠利用這一新技術來重新詮釋熱力學中的温熵關係？這就涉及如何在量子力學框架內重新定義熱，量子熱力學這一古老命題因此重煥生機。

撰文 | 姚堯（華南理工大學物理與光電學院）

來源 | 選自《物理》2024年第2期

01 引言

四大力學都有其經典與量子相對應。經典力學對應量子力學，經典電動力學對應量子電動力學，經典統計力學對應量子統計力學，經典場論對應量子場論。唯一的例外就是經典熱力學，目前通常的物理專業課程中還沒有量子熱力學。

在國際單位制中有7個基本單位，其中6個已經可以在微觀的原子層面定義。唯一的例外是温度，定義它所採用的玻爾茲曼常數，或者水的相變點，是相對宏觀的。我們還無法採用一個更加微觀的實驗手段來定義温度。

按照熱力學的語言，温度反映的是分子的平均動能，而那些難以定義動能的系統，比如自旋系統，它的温度依賴性在這個定義下顯得非常晦澀。又或者按照能均分定理，每一個自

系綜理論將系統的温度歸結為由環境來決定，但環境本身是一個相對模糊的概念，環境的温度由誰來提供，沒有解釋。

歸根結底，熵難以被實驗測定是根本原因。因為強度量一般難以向微觀推廣，除了温度，壓強、化學勢的測定方法也相對宏觀唯象。作為與温度相對應的廣延量，如若熵能在微觀層面被準確測定，我們就可以利用能量對熵求導來獲得温度。然而經典統計力學利用狀態數來定義熵，令這一想法難以實施。

近年來，伴隨着量子信息的迅速發展，測量糾纏熵已經不存在原則性的技術障礙。是否能夠利用這一新技術來重新詮釋熱力學中的温熵關係呢？這就涉及如何在量子力學框架內重新定義熱，量子熱力學這一古老命題因此重煥生機。

02 自由能與温度

曾經，蘇聯在熱力學的研究中走在世界前列。在朗道的唯象理論中，自由能是熱力學的核心物理量，所有系統都要向自由能最小的狀態演化，正如力學系統總會選擇作用量最小的運動路徑一樣。而自由能是温度的函數，只要能準確測量自由能，温度的確定就是題中應有之義。自由能是刻畫熱平衡狀態的特性函數，按照導出經典漲落—耗散定理的慣例，我們需要找到一個能將平衡態與非平衡態聯繫起來的辦法。20世紀90年代發展起來的量子漲落理論，就是在平衡態的自由能與非平衡態的不可逆功之間建立聯繫，從而通過測量功來確定自由能。

對於一個絕熱系統，如果其能級從En躍遷到Em，則可以定義外界對其做功為W=Em-En。現若假定躍遷的初態和末態均處於熱平衡狀態，並且躍遷過程發生的概率分佈函數為R(W)，利用細緻平衡原理不難推得所謂的Crooks關係[1]：

其中ΔF是末態與初態的自由能之差，R’ 為反向做功概率。這個關係中做功會發生漲落，因為功是與路徑有關的過程量，所以如果我們對所有可能的做功路徑取平均，就得到著名的Jarzynski等式[2]：

乍一看，Jarzynski等式與經典熱力學中自由能與做功最小值的關係有相似之處，然而經典熱力學的自由能需要在近平衡狀態討論，以確保整個過程可逆。Jarzynski等式對可逆性不做要求，任意偏離的平衡態原則上都是允許的。當然，e指數必然會放大實驗測量時的誤差，導致某些反向做功的路徑影響更加顯著。

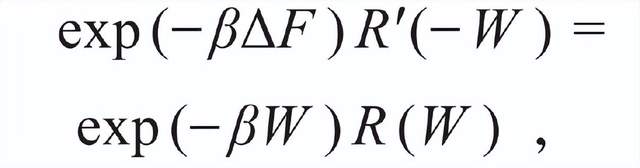
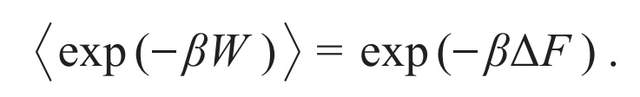
在Jarzynski等式被提出來以前，人們更多的是採用路徑積分對自由能的處理方式，也就是將温度看作虛時間，並將其作為演化的另一個維度。這跟經典熱力學的定義並不自洽，因為等温—絕熱過程在卡諾熱機中被認為是可逆的，它無法用來定義時間之矢。如今我們在量子漲落理論的框架下，利用不同能級狀態之間相干性的變化，可以將温度之矢定義為量子系統的固有演化方向，從而為熱的量子化提供新的詮釋，這正是下面要談的量子資源論的主要研究思想。

2002年發表在Science雜誌上的一個工作驗證了Jarzynski等式[4]。他們利用純機械的方法將摺疊的核糖核酸強行展開，通過測量施加的力來確定相應的功，並與自由能對比。此後，在蛋白質、聚合物、冷原子、離子阱等諸多實驗體系中，均以不同形式驗證了這一等式的合理性。筆者認為，Jarzynski等式是量子熱力學一個很好的切入點，未來我們不妨用DNA或其他更具標誌性的生物大分子作為測量自由能的“標準器”，並據此定義更加微觀的温度，作為基本物理量使用。

自伽利略發明温度計至今，人類對於温度的研究已有四百多年，早於電、磁、光等其他學科。從熱電偶到紅外線，人類的測温手段日益豐富，然而橫向對比其他幾門學科，電已能夠小到皮安，磁已能夠弱到高斯，光已能夠短到阿秒，而即使目前最先進的測温控温設備，其温度仍在小數點後第一位來回跳動，和四百年前幾無進步。發展新的微觀測温方案，我們需要全新的理論框架。

03 量子混沌

量子熱力學最核心的理論體系是在量子混沌理論的基礎上建立起來的，目前常見的文獻中，關於量子混沌的名稱通常表述為quantum chaos[4]。Berry當年曾使用quantum chaology，用以區分全量子系統的混沌效應，這個詞偶爾會出現在文獻中，但未廣為接受。我們現在通常研究的量子混沌，是指將量子系統經典化或半經典化後的混沌，後者是指將原子核部分經典化，再與經典混沌相比較。全量子系統的混沌研究目前未有重大進展。

在經典力學中，與混沌相對應的概念是可積。當一個運動系統的自由度與守恆量 (運動積分) 的數量一致時，其運動方程是可積的 (可解的) 。相反，若找不出足夠數量的守恆量，則該系統是混沌的。一般地講，由於能量守恆總是先驗成立，故而一維經典體系總是可積的。若再加上角動量守恆，則二維體系也可積，比如開普勒行星模型。但若二維體系有特殊的邊界，比如圖1所示的是混沌理論中經常作為出發點的L. A. Bunimovich體育場 (stadium) 模型[5]，其形狀如一個田徑運動場，這種情況下無法找到第二個守恆量，則會出現混沌。除此以外，非微擾三體系統也因找不到足夠的守恆量而成為混沌，比如水分子的三個原子、質子的三個夸克等，這是流體力學、核物理中時常發生混沌現象的原因。至於三維，不可積的情況更為常見，所以絕大多數自然系統都是混沌的，可積系統只是少數。

圖1 體育場模型

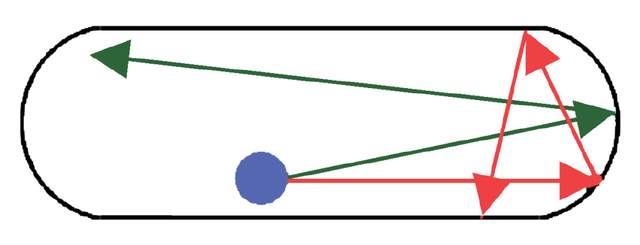
將這些經典混沌的概念向量子推廣的研究早在van Vleck時就有了，但真正的進展發生於1950年代後。Wigner等人首先用隨機矩陣理論來處理量子混沌，然後是Gutzwiller等人提出跡公式 (trace formula)，跨出了經典混沌量子化的關鍵一步。1980年代以後，隨着原子分子光學的發展，尤其是對電磁場中氫原子動力學行為的研究，揭示出量子混沌已經是無法迴避的問題，隨機矩陣與跡公式這兩套理論均得以迅速發展，形成較為完整的理論體系。

關於混沌的定義，一般應滿足如下三個條件：

(1)有界性 (boundedness)：其運動範圍存在一個確定的邊界；

(2)迴歸性 (recurrence)：無論從哪個起點出發，總能不斷回到該起點；

(3)指數敏感性 (exponential sensitivity)：兩條起點任意接近的軌跡總是以指數形式分離。

第一條提示了要形成混沌必須有確定的勢場或相互作用來約束系統的運動，排除了完全自由的系統中存在混沌的可能。第二條提示了不存在不穩定的初始狀態，比如從高空拋下一個物體，從地面反彈後無法回到原位，則不是混沌的。一般人更熟悉的“蝴蝶效應”則是指第三條。在經典混沌中，一般定義

，其中δ(t)是兩條起點相互接近的運動軌跡之差，ξ是Liapunov指數，它為正時就是混沌的。由於運動軌跡有界，所以δ(t)隨着時間演化並不會無限增加，而是會逐漸趨於飽和，所以為了真實反映指數敏感性，在實際計算時往往要映射到正切空間，也就是運動軌跡的導數所張成的空間。

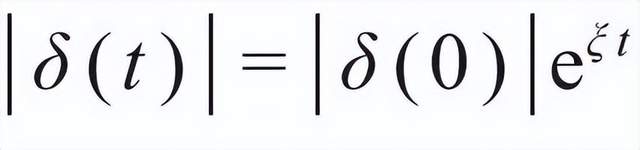
值得一提的是，Liapunov指數是經典混沌理論的概念。在量子力學的框架下，如果波函數嚴格按薛定諤方程演化，即使在正切空間中也很難看到δ(t)隨e指數發散的行為。按照Ehrenfest對此的解釋，需要定義一個切斷時間 (break time)，在這個時間內，量子體系的演化應當與經典混沌對應，反之則不存在混沌的現象。最初，切斷時間被認為就是普朗克時間，但隨着理解的深入，這一定義越來越不被認可。

第二種常用的鑑別混沌的指標是描述迴歸性的龐加萊映射。從高維的空間切出一個任意的平面，運動軌跡每穿過該平面一次，就在這個平面上打一個點。足夠長時間後，規則的兩體系統只會出現極少數的點，微擾的三體系統會出現一些有規律的曲線，混沌系統則會遍歷整個平面，這正是用來理解各態歷經的常用圖像。

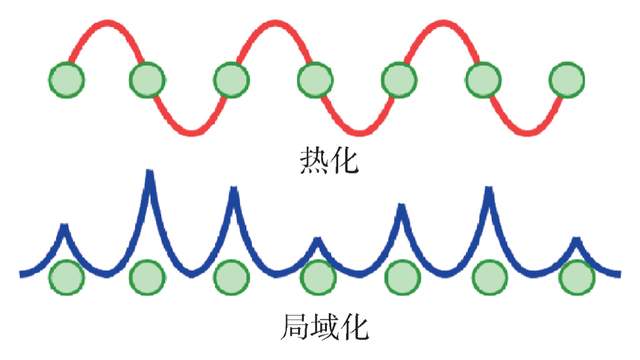
目前針對量子混沌的研究中，使用最多的指標是能級分佈。由於可積性的差異，混沌系統的能級是互斥的 (level repulsion)，而可積系統則是聚簇的 (level clustering)。前者的能級間距表現為高斯分佈，後者表現為泊松分佈，這是用來分辨量子熱化態與局域態的重要指標。能級互斥正是自然界去簡併傾向的體現，因此絕大多數自然系統傾向於混沌與熱化，這是我們將熱力學量子化的理論基礎。

04 量子熱機理論

2008年，M. Rigol等人在Nature雜誌上發表文章[6]，翻開了量子熱化領域全新的一頁，這套全新的理論現在一般被稱為本徵態熱化假説 (eigenstate thermalization hypothesis，ETH) 。

量子熱化理論的出發點，是為量子多體系統建立一個新的吉布斯系綜，通常叫做廣義吉布斯系綜 (generalized Gibbs ensemble，GGE)。它的核心思想不再是像傳統量子統計那樣以某些微觀粒子作為系統，而是以相空間中的一個局域空間範圍作為系統，這是最核心的視角轉變。在這個新視角下，能量狀態的不可區分性可以用來取代微觀粒子的不可區分性，從而可以在微觀狀態的層面重新定義熱化。

圖2 三維空間中的系統

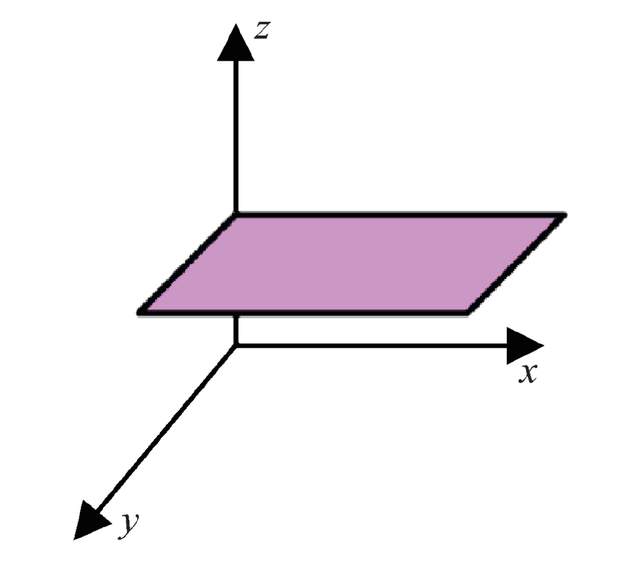
在經典統計的圖像中，如圖2所示，要想從整個宇宙的相空間裏分離出一個我們感興趣的系統，需要把這個系統的全部自由度拿出來，就像龐加萊映射，在一個三維xyz的空間中把一整個xy截面全部抽出來，構成一個系統。我們不能只截取這個空間內的一個局域範圍，比如一個小方塊，因為它並不包含完備的自由度。然而在量子熱化理論中，例如一維x方向的鏈，我們可以只抽取其中若干個格點作為系統，不用把整個一維鏈 (x方向自由度) 全部拿出來。

當我們把相空間中某個局域範圍 (而不是某個粒子) 作為系統，剩下的範圍作為環境，環境通過與系統的耦合破壞系統的某些對稱性，使得系統可能到達的相空間 (自由度) 得以擴大，這些新自由度正是由環境提供或者映射到系統上的。反映在量子測量論中，就是環境扮演一個宏觀測量者的角色，通過測量打開系統的新自由度，用數學語言來講就是環境的某些算符與系統的哈密頓量不對易，從而不能為系統找到足夠多的局域運動積分。

由於不再將單個粒子當作系統，而是將局域的空間當作系統，所以許多經典熱統的觀念都要有所轉變。比如，經典熱力學通常認為空間勢能的無序度越高越容易熱化，經典混沌理論也這樣認為。量子熱化理論則相反，空間越無序越容易局域化，從而難以熱化。因此，我們不能再像經典混沌那樣以全局的守恆量，比如能量、動量、角動量等來作為判斷是否可積的標準。在量子熱化理論中，即便我們能找到足夠多的全局運動積分，對應於經典可積的情況下，系統仍然有可能是熱化的。我們要尋找的是局域運動積分 (local integral of motion)，它們的數量與局域狀態數的關係，決定了一個系統是熱化的，還是局域化的。

不同局域運動積分之間理應互相對易，比如不同格點的自旋算符總是對易的，所以整個哈密頓量未必會存在簡併性。按照量子混沌理論，這應該是熱化的情況。的確如此，即使存在局域運動積分，環境對系統對稱性的破壞作用仍非常普適，這也是熱化發生於絕大多數系統的原因。簡併性的保護需要在局域運動積分的基礎上，進一步引入對稱性、拓撲、多體相互作用等其他因素。

ETH和經典統計中的各態歷經假説究竟有什麼不同？筆者認為，ETH最大的優點並不在於它描述了“絕大多數”系統的行為，而是它給出了不滿足各態歷經的明確條件。各態歷經雖然是經典統計的基本假定，但它不同於其他物理理論，其預測性差，又難以證偽，總是會產生各種似是而非的結果。而在ETH的定義中，對於先驗成立的各態歷經假説，我們有了可以定量證偽它的方案，這是了不起的進步。

05 局域化

提到局域化一詞，很容易想到的是安德森局域化。然而，赫赫有名的局域化在很長時間內其實都未成為顯學，國內許多“固體物理”課程中，“局域化”三個字基本是一筆帶過。零星的研究以導電機理為主，有不少人進入該領域是基於安德森、莫特等人的名聲。基於歷史傳統，固體物理中研究更多的是晶體物理，用能帶和能隙來區分金屬、半導體和絕緣體是物理學家更習慣的思考方式，做第一性原理計算時，晶胞總是儘可能取小以減輕計算量。如圖3所示，局域化的研究需要在格子模型中引入無序，破壞平移對稱性，這與晶體的計算並不完全相容。由此，局域化在很長時間內都像是化學語言。化學家不執着於晶體，更關注無序所帶來的載流子局域化，並發展出諸如極化子遷移之類的導電機理。利用Marcus理論、勢能面躍遷等半經驗理論，化學家在一定程度上能處理好導電的量子性問題。

圖3 熱化與局域化

如今，局域化被提升到物質科學最本原的程度來研究，脱離了金屬—絕緣體轉變等具體問題的束縛，是物質科學家們對量子熱化理論的回應。研究局域化的核心正是尋找量子資源，是找到推動人類進步的新材料。如果萬物都會被熱化，物質科學家們也要致力於找出那萬分之一不會被熱化的量子物質。

能帶的出現是不同原子上原本簡併的局域軌道在電子動能的作用下發生了去簡併效應，也就是發生了熱化，從而形成能級互斥。化學上，這是成鍵和反鍵軌道形成的原因。即使我們將任意雜質放進體材料中，該雜質的能級出現在能帶裏面，雜質軌道仍然會與母體材料中的原子軌道雜化，使我們看不清雜質和母體的區別。要想破壞熱化，或形成局域化，必須要有一些非凡的物理因素出現。總結起來，可歸結為如下幾種情況。

第一種情況是派爾斯不穩定性，通過在一維體系中引入晶格原子微小振動，在原本的能帶中劈裂出新的能隙，並在能隙內部形成隙間態，例如孤子、極化子等。一般認為，一維體系中即使再弱的無序也會導致局域化，這就是“一維體系無金屬”定律。這與混沌理論自洽，因為維度越低越難以熱化，即使是哈伯德模型這樣平移簡併的局域軌道在電子動能的作用下發生了去簡併效應，也就是發生了熱化，從而形成能級互斥。化學上，這是成鍵和反鍵軌道形成的原因。即使我們將任意雜質放進體材料中，該雜質的能級出現在能帶裏面，雜質軌道仍然會與母體材料中的原子軌道雜化，使我們看不清雜質和母體的區別。要想破壞熱化，或形成局域化，必須要有一些非凡的物理因素出現。總結起來，可歸結為如下幾種情況。不變的系統，也只能是弱熱化。

上述局域化本質上都是單電子圖像，而強關聯體系中由於多體相互作用的存在，一些簡併性無法被去除，能級無法互斥，不再是嚴格意義上的量子熱化態，也無法寫成任何廣義吉布斯系綜形式的局域化，這就是所謂的多體局域化 (many-body localization，MBL)。這個詞最早出現於2006年D. M. Basko等人發表在Annals of Physics上的文章[8]。不過早期工作仍以安德森局域化的框架為主，只是傳統模型的簡單推廣。真正產生影響力是在量子熱化理論成名以後，量子統計和凝聚態理論開始深度融合，多體局域化與量子熱化成為相互對應的名詞，並廣泛“出圈”。

早期的多體局域化研究沿襲熱化理論的習慣，主要探討能級分佈。通過建立一個多體相互作用模型，加上無序勢，計算其本徵能級分佈是互斥的還是聚簇的，若為前者則是熱化，若為後者則是多體局域化。這樣做的最大問題，是難以與熱化中的預熱化、局域化中的安德森局域化相區分。隨後就出現了第二類研究方案，即量子淬火動力學，淬火會導致有限尺寸的局域孤子出現，這是研究局域化非常好的出發點。在此基礎上，一個完全超越預期的現象被發現，那就是糾纏熵的對數傳播。

在安德森局域化中，局域態之間的相互作用是e指數衰減的，即互相之間完全隔絕，不會發生任何信息傳播。但在多體局域化中，J. H. Bardarson等人的數值計算結果表明[9]，糾纏熵會在很長時間內以對數形式緩慢增長。這一結果在許多計算中得以證實，被確認為多體局域化最關鍵的動力學特徵，它反映了局域態之間存在着等效長程相互作用。這是一個令人振奮的結果，意味着量子計算可以在不改變局域態布居數，也就是能量的情況下，傳播量子信息。

於是，在多體局域化應用到量子計算的探討中，有了局域比特 (l-bit) 的概念。所謂局域比特，其實就是局域運動積分，它們是能夠長時間保持不變的局域守恆量。以經典的伊辛模

由於離散能級和局域比特的存在，多體局域化系統的本徵態必然是局域態，這些局域態一定會發生自發對稱性破缺。局域比特如果是一個自旋，它只可能處在朝上或朝下的某一個態，雙態之間無法轉換。基態則是這些局域比特所形成的長程序，因此多體局域相也被稱為本徵態有序相。或許未來我們可以用多體局域化來統一解釋強關聯體系中複雜的相變問題。

06 量子熱機

當我們測量一個處於基態或熱平衡狀態的系統，只要這個測量手段與維持系統處於熱平衡的算符不對易，系統立即進入非平衡狀態。經典熱力學通過漲落—耗散定理，將這一非平衡過程近似為一系列準平衡過程，從而將熱與功簡單聯繫起來。但正如Rolf Landauer那句名言：“Information is physical”，量子測量在提取信息時所消耗的能量，比經典熱機的熱功轉換要深刻得多。正是基於這一原因，有不少人認為量子熱力學就是研究量子熱機的學問。

最早關於量子熱機的研究從20世紀50年代就有了[10]。但那時的討論保留了大量經典熱機的特徵，與現在的量子熱化和局域化理論並不自洽。那時的核心任務就是將經典Otto熱機量子化[11]。Otto熱機即標準的四衝程內燃機，包含等容吸熱、絕熱做功、等容放熱、絕熱回覆四個過程。由於量子力學不能很好地定義温度，故而Otto熱機比包含等温過程的卡諾熱機討論起來更為便利。

由此可見，要想在量子體系中實現等容過程，就要保持本徵能譜不變，只讓不同能級的布居數發生變化，也就是在不同本徵態之間非絕熱轉換。要想實現等熵 (絕熱) 過程，則要保持布居數不變，只改變相應的本徵能量。如圖4所示，以一個無限深方勢阱為例，初始狀態時粒子處於基態，經過一個等容吸熱過程，本徵能量保持不變，粒子從低能級轉移到高能級。然後，勢阱變寬，體積變大，本徵能級下降，相當於絕熱過程對外做功，之後粒子經等容放熱過程重新回到基態，如此就構成了量子Otto熱機工作循環。

圖4 量子Otto熱機工作循環

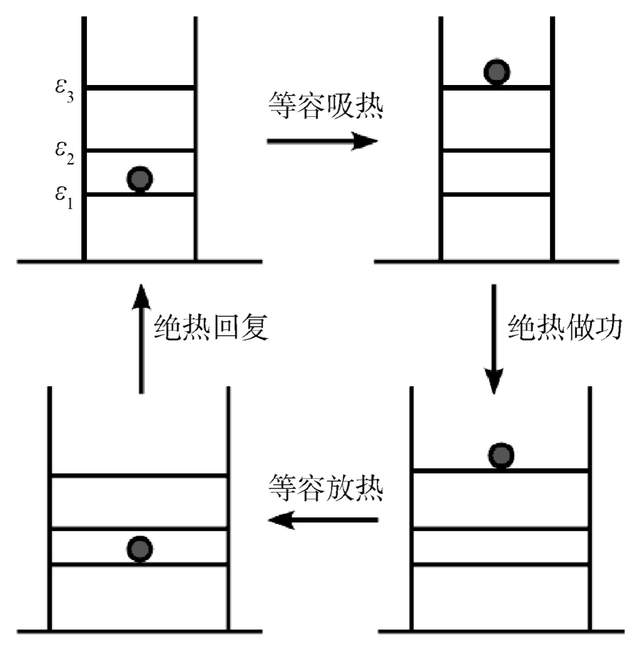
這只是一個為了形式上與經典Otto熱機對應的玩具模型，並不具備實用性，粒子無法自發推着勢阱的邊界往前走。真正有實用性的量子熱機模型，最簡單的工質是三能級系統，高温和低温熱源均是單頻的玻色子庫。在旋轉波近似下，一個玻色子庫與工質之間會形成二能

由於對熱的微觀認識仍不充分，即使在三能級系統這樣有着明確本徵能譜的系統中，對外做功過程的模擬仍存在相當大的技術難度。量子動力學無法模擬整個工作循環，甚至單次熱功轉換都難以模擬，所以常見做法是通過外加含時的驅動場，將能夠對外做功的活性態 (active state) 和不能對外做功的被動態 (passive state) 區分開來，相當於功被三能級系統這樣的工質儲存起來，工質扮演了電池 (battery) 或飛輪 (flywheel) 的角色。在量子熱機中，這種系統工質的作用稱為功貯藏室 (work repository) ，其中可以被提取出來的最大功被稱為ergotropy，該詞尚無統一中文譯名。

將經典熱機反向操作，就是一台吸收式製冷機 (absorption refrigerator)。然而，量子製冷機並不能簡單地將量子熱機反向，這涉及自發對稱性破缺和信息擦除的複雜問題。目前，研究者已經設計出了各種有趣的量子製冷機，比如給一個四能級系統接上三個庫，其中兩個扮演低温熱源，另一個扮演高温熱源，類似於量子光學中的雙光子吸收。具體內容不再贅述。

若説研究局域化是致力於破壞空間平移不變性，研究時間晶體就是破壞熱力學第一定律，那麼討論量子熱機的出發點就是致力於破壞熱力學第二定律，也就是熵增原理。在經典熱機中，熵的作用永遠是負面的，擁有最高效率的理想熱機必須保持全過程可逆，熵保持不變。量子熱機的本質就是要探討將熵作為正面資源加以利用。要麼是直接與能量或功相互轉換，要麼是以量子相干性作為催化劑 (catalyst)，間接促進有用功或ergotropy的增加。

這正是經典熱力學中的麥克斯韋妖。常見的實現麥克斯韋妖的裝置包括費曼棘輪、Lochmidt回波等。在所有可能的選項中，20世紀20年代出現的Szilárd熱機最具啓發性。所謂Szilárd熱機，是指當一個盒子裏只有一個分子時，若分子在盒子左邊，讓右邊對外做功，當分子在右邊時，讓左邊對外做功。由於總是真空的一邊在做功，能量損耗可忽略，就相當於從單一的等温環境中提取了有用功，粗看上去的確違背第二定律。

2010年，S. Toyabe等人發表在Nature Physics上的一篇文章據此設計了一個有趣的實驗裝置[12]。他們將兩個直徑為287 nm的聚苯乙烯塑料顆粒吸附在塗抹了親和劑的玻璃襯底上，兩個顆粒結合形成類二聚體結構，具有面內旋轉自由度。之後將它們放置在一個精巧設計的四極電場內，通過向四個電極加入橢圓旋轉的交變電場，可以讓這個二聚體旋轉起來。二聚體很小，它的旋轉具有隨機性。一直由顯微鏡在實時觀察整個系統，當某時刻二聚體所處的旋轉角度正好處於電勢的波峯處，就會開啓一個反饋電場，讓輻角反向，二聚體會因能量降低而掉到波谷中。如此反覆操作，二聚體的旋轉就會呈現出單向演化的特徵。

這個裝置看上去並沒有對分子做功，與麥克斯韋妖的設想相一致。但仔細分析會發現，要實現上述操控需要對納米顆粒的微觀運動實時瞭解。無論是顯微鏡、圖像識別，還是反饋電場的引入，都需要巨大的能量消耗，其作用不是讓納米顆粒運動，而僅是知道它的實時運動信息。事實上早在Szilárd熱機的討論中人們就已經明白了這一點，信息的獲取本身是需要能量的，這正是Landauer那句名言要表達的含義。

07 量子資源論

物理定律的本質就是限制和約束 (constraint)，比如運動速度不能超過真空光速，能量不能從無到有等。所謂的資源論，就是研究如何對這些客觀限制加以利用。量子力學更加註重對稱性和守恆律，所以在將熱力學量子化的過程中，資源論也應當被量子化[13]。

資源論最早是2000年由D. Janzing等人引入到物理學中[14]，其出發點是在當時如火如荼的冷原子技術。人們醉心於讓原子的温度越來越低，但卻忽視其代價。相比於單個原子，讓它冷卻的激光器和其他裝置極其龐大，所消耗的能源難以計數。如果以冷原子實現的量子計算機當作一台量子熱機，那麼其效率必然極低。我們究竟能以多小的代價來冷卻原子呢？尋找這個極限是量子資源論的出發點。

量子資源論之所以不沿用量子信息論的名稱，主要是為了探討信息與能量之間的轉換，特別是如何將量子“相干性”作為資源來使用，而不是直接耗散掉，未來可能的工業革命極有可能發生在對相干性這種新能量形式的使用上。傳統熱力學以熵或自由能作為基礎物理量，它們的單向演化定義了熱力學過程的不可逆性。量子資源論則要探討，一個量子系統會自發選擇怎樣的演化方向，我們需要為此定義一組 (不再是一個) 新的物理量對其演化加以限制。

用到的數學工具就是線性代數中的完全正定保跡映射 (completely positive trace-preserving map)。所謂完全正定，是指該映射作用到某算符上，作用前後該算符均是半正定的，半正定的意思就是它作用到任意態矢量上所得的內積為非負。假設某個系統S的狀態用密度矩陣ρ表示，引入一個處於熱平衡狀態γ的環境R，使之與ρ直積並共同演化，再將環境部分求跡，即定義如下超算符：

其中，ρT是熱平衡分佈。第二項就是經典自由能，第一項則是由量子相干性的變化導致熵變所引起的自由能變化。這裏的α有很多取值，所以可以有很多個不同的自由能，它們共同形成對量子體系演化方向的限制。如何將這一部分自由能加以利用，是量子資源論的重要研究課題。

其中最值得關注的莫過於非對稱性 (asymmetry) 理論。所謂非對稱性，就是指ρ當中包含了

這樣的在某個對稱表象下的非對角元，也就是疊加態。最常見的當然就是時間平移不變性所對應的能量表象，對角元在時間演化算符作用下完全保持不變，所以叫對稱態，對稱態可以是純態也可以是混態。而非對角元在時間演化時會增加一個相位，所以是破壞平移不變性的非對稱態。根據熱操作的單調性可以發現，最均勻的疊加態通常只能作為熱操作的初態，而很難作為末態。這種難以被熱操作自然演化而製備得到的非對稱態，就是“昂貴的”資源，與之相反，不均勻的疊加態則是“廉價的”，能量本徵態則是“免費的”。非對稱性理論，可以幫助我們回答一個基礎但懸而未決的量子力學問題：能量本徵態的線性疊加態究竟是如何產生，又應如何被利用。此外，在非對稱性理論的幫助下，我們還可以將糾纏的提純與形成過程組成一個量子熱機的循環，從而研究如何將量子相干性作為資源加以循環利用。

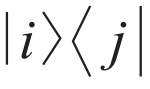
08 通向萬物理論之路

物質科學的發展歷史上，無數人追尋着萬物理論 (theory of everything) 的光芒：通過一組方程描述所有已發現的現象[15]。曾經，金茲堡—朗道理論被認為最接近這一目標。它以自由能作為判據，通過自發對稱性破缺達到最終物態，不僅被成功運用於常規超導，還被廣泛運用到各種其他物態。然而隨着高温超導、分數量子霍爾效應等新奇凝聚態物相的發現，這套理論體系不再普適成立[16]。量子液體、強關聯、拓撲序、量子熱化等一系列新理論不斷被提出以解釋這些新奇物性。

量子信息的發展對萬物理論的探索形成了一條全新賽道。過去，人們無論研製出多麼先進的表徵儀器，對於物質內部微觀層面發生的物理仍然需要大膽假設、小心求證。量子模擬則可以先理論後實驗，通過事先設計來實現新奇物相，這是一條前所未有的研究新思路，正如Nature Physics的一篇新聞標題講的：“Measurements make the phase”[17]。

當熱力學第二定律剛被提出時，熵被認為是人類對宇宙無知的程度，後來與信息論相結合，熵也因此被賦予了信息量的物理內涵。從這個意義上講，只要還存在熵這個物理量，萬物理論似乎就不應該存在。但是現在，糾纏熵作為一個可觀測量已經滲透到物質科學研究的方方面面，基於糾纏的理論極有可能在未來扮演萬物理論的角色。在那之前，關於熱的定義是否還應當與熵掛鈎，需要更加仔細研究。

不僅是熱，粒子數是否一個多餘的概念？化學勢與温度是否同一個物理量？這一類問題近年來也被廣泛探討[18]。隨着拓撲弦等圖像逐漸將基本粒子囊括進糾纏的理論體系中，這樣的探討會更加深入，並逐漸建立起真正具有量子化特徵的熱力學理論，那也將是更具革命性的萬物理論。

參考文獻

[1] Crooks G E. Phys. Rev. E，1999，60：2721

[2] Jarzynski C. Phys. Rev. E，1997，58：5018

[3] Liphardt J，Dumont S，Smith S B et al. Science，2002，296：1832

[4] Haake F. Quantum Signatures of Chaos. 2nd edition，Springer Series in Synergetics. Berlin：SpringerVerlag，2001

[5] Bunimovich L A. Commun. Math. Phys.，1979，65：295

[6] Rigol M，Dunjko V，Olshanii M. Nature，2008，452：854

[7] Nandkishore R，Huse D A. Annu. Rev.Condens. Matter Phys.，2015，6：15

[8] Basko D M，Aleiner I L，Altshuler B L. Annals of Physics，2006，321：1126

[9] Bardarson J H，Pollmann F，Moore J E. Phys. Rev. Lett.，2012，109：017202

[10] Lande A. Phys. Rev.，1952，87：267

[11] Kosloff R，Levy A. Annu. Rev. Phys. Chem.，2014，65：365

[12] Toyabe S，Sagawa T，Ueda M et al. Nat. Phys.，2010，6：988

[13] Goold J，Huber M，Riera A et al. J. Phys. A：Math. Theor.，2016，49：143001

[14] Janzing D，Wocjan P，Zeier R et al. Int. J. Theor. Phys.，2000，39：2717

[15] Laughlin R B，Pines D. PNAS，2000，97：28

[16] Wen X G. National Science Review，2016，3：68

[17] Ware B，Vasseur R. Nature Physics，2021，17：294

[18] Khemani V，Vishwanath A，Huse D A. Phys. Rev. X，2018，8：031057

本文經授權轉載自微信公眾號“中國物理學會期刊網”，原文標題為《熱力學與量子力學在21世紀重新相遇》。

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。