洛侖茲座標變換的障眼法_風聞
guan_15685916721577-53分钟前
洛侖茲座標變換的障眼法
一、強詞奪理障眼法
其次我們必須注意,洛侖茲變換與伽利略變換的前提是不一樣的。洛侖茲變換隻承認相對性原理和光速不變原理,其他的(如時間是否絕對、兩座標系是否有一致的尺度等等)一概不管,都作為需要求解的部分進行推導,最後是什麼樣就是什麼樣。伽利略變換隻承認絕對空間和絕對時間,其他的(如光速是否一致、速度如何相加等等)一概不管作為要求的量進行推導,最後得出什麼結論就是什麼結論。因此,在洛侖茲變換中,我們沒有任何理由認為兩個座標系的時間與空間尺度必須是一致的,它們完全是和所有未知量平等的量,不能具有任何優越性,就像在伽利略變換中不能認為光速具有任何優越性一樣。因此,永遠不要用洛侖茲變換去證偽伽利略變換的結論,也永遠不要用伽利略變換去證偽洛侖茲變換的結論。這兩種變換在它們各自內部的邏輯都是自洽的,説“哪個是真,哪個是偽”只能看它們哪一個和實驗結果符合得更好。
二、數學推導分步障眼法
第一部分
1、利用光速C和正反向運動建立座標的光速關係式
對於一個從K原點出發朝X軸正方向前進的光信號,我們有X=CT或X-CT=0 (1a)
而若光信號是沿着X軸負方向前進的,則有-X=CT或CT+X=0 (1b)
此時,我們實際上是選取了一些特殊的點,使得它們的座標滿足X-CT=0或CT+X=0,實際上這些點就是從原點出發的光信號末端經過的點。
這些點對應到K’中,因為光信號相對於K’也以光速傳播,所以有
X’ -CT’=0 (2a)
或X’ +CT’=0 (2b)。
特別説明:注意這裏是座標與光速的關係式。
2、利用光速C和正反向運動即待定係數建立關係式(3)和(4)
X**’** -CT**’**=λ(X-CT) (3)
X**’** +CT**’**=μ(X+CT) (4)
特別説明:關係式(3)和(4)左邊的光速C應該有光源運動的光速C。我們暫計作C,+V。
3、1 利用關係式(3)加(4)聯立解消去有光源運動的光速C(我們暫計作(C,+V)。得方程:
X**’**=(λ+μ)X/2-(λ-μ)CT/2
特別説明:從上式分析,如果將待定係數加入等式左邊,則等式變為:
X=(λ+μ)X,/2-(λ-μ)(C,+V)T/2
3、2利用關係式(4)減(3)得方程:
(C,+V)T**’**=-(λ-μ)X/2+(λ+μ)CT/2
3、3利用2、1和2、2所得方程
4、利用換元法得方程
a=(λ+μ)/2
b=(λ-μ)/2
X,=aX-bCT
5、將上面方程聯立得方程組(5):
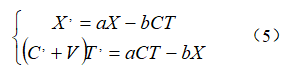
特別説明:從方程組(5)可以看出,第一個方程的左邊已經是不包含有光源運動的光速C。
6、取值障眼法
第二部分
到目前為止,我們只用了已知量X、T和常數c、a、b,而沒有涉及到兩座標軸的相對速率V。而我們知道,將座標變換時不可避免地要使用到V。這一部分的討論便是把V用方程組(5)中的已知量表示出來,從而將V引入變換羣方程。
此處有一點很重要:顯然,K’上所有的點都相對於K以恆速率V運動,所以,在對V進行描述時,K’上所有的點都是平等的!即我們可以描述K’上任意一點相對於K的位置變化情況,從而確定V。因此,我們選取最簡單的點——K’的點O’座標應為(0、T’),即X’=0。我們把這一個值代入(5)的第一個方程中(即在(5)的基礎上,賦予X’、T’、X、T以這樣的意義:X’和T’、是K’原點O’座標,X和T是O’在K中對應的座標),有:
aX-Bct=0
aX=Bct
X=Bct/a (6)
特別説明:利用取值X’=0得(6);式。(因此,我們選取最簡單的點——K’的點O’座標應為(0、T’),即X’=0。)
7、相對速度V代入障眼法
那麼,我們已經賦予X’為K’原點的意義,所以X自然就是O’在K中對應的座標。X、T都是在K上觀察而言,那麼顯然,對於O’的對應點,有
X=VT
所以我們得到
V=bC/a
這樣,我們便把V引入了關係式中。
特別説明:這裏的相對速度V的代入是一個小學數學錯誤。因為這裏的X=VT。而建立關係式的時是X=CT。
我們將X=VT提前代入前面的關係式得:
VT=CT或VT-CT=0 (1a提前代入X=VT)
-VT=CT或CT+VT=0 (1b提前代入X=VT)
從提前代入的結果看,洛侖茲座標變換是完全錯誤的。
將推導的一段抄錄如下:
(對於一個從K原點出發朝X軸正方向前進的光信號,我們有X=CT或X-CT=0 (1a)
而若光信號是沿着X軸負方向前進的,則有-X=CT或CT+X=0 (1b)
將X=VT提前代入(1a)和(1b))
後面還有取值的強詞奪理,在這裏略。