打破內存牆_風聞
半导体行业观察-半导体行业观察官方账号-专注观察全球半导体最新资讯、技术前沿、发展趋势。46分钟前
**摘要:**前所未有的無監督訓練(unsupervised training)數據以及神經縮放規律(neural scaling laws),導致模型規模和服務/訓練 LLM 的計算需求空前激增。然而,主要的性能瓶頸正日益轉向內存帶寬。
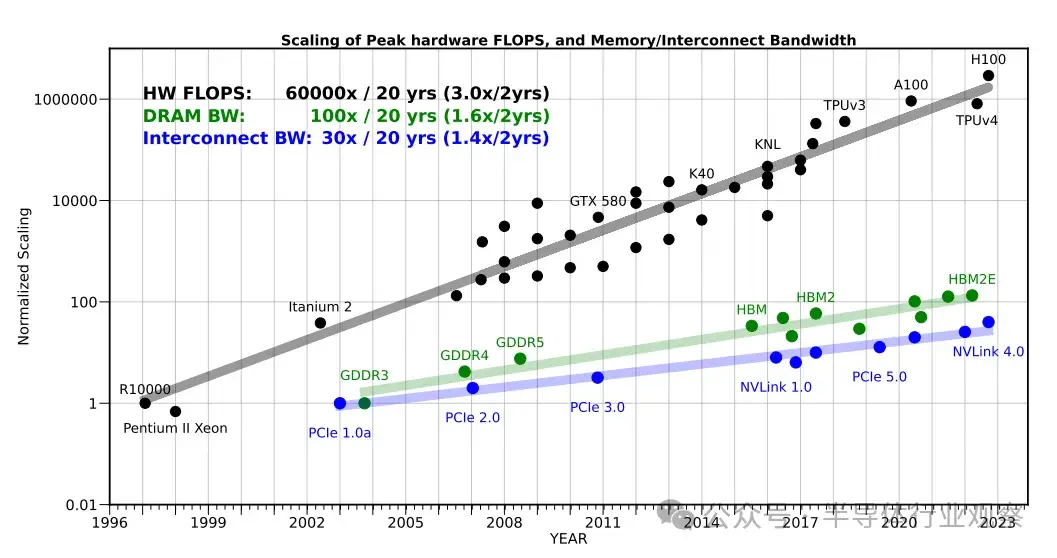
在過去 20 年中,服務器硬件 FLOPS 峯值以 3.0 倍/2 年的速度增長,超過了 DRAM 和互連帶寬的增長速度,而 DRAM 和互連帶寬的增長速度分別僅為 1.6 倍/2 年和 1.4 倍/2 年。這種差距使內存而非計算成為人工智能應用的主要瓶頸,尤其是在服務領域。
在此,我們分析了編碼器和解碼器 Transformer 模型,並展示了內存帶寬如何成為解碼器模型的主要瓶頸。我們主張重新設計模型架構、訓練和部署策略,以克服內存限制。
引言
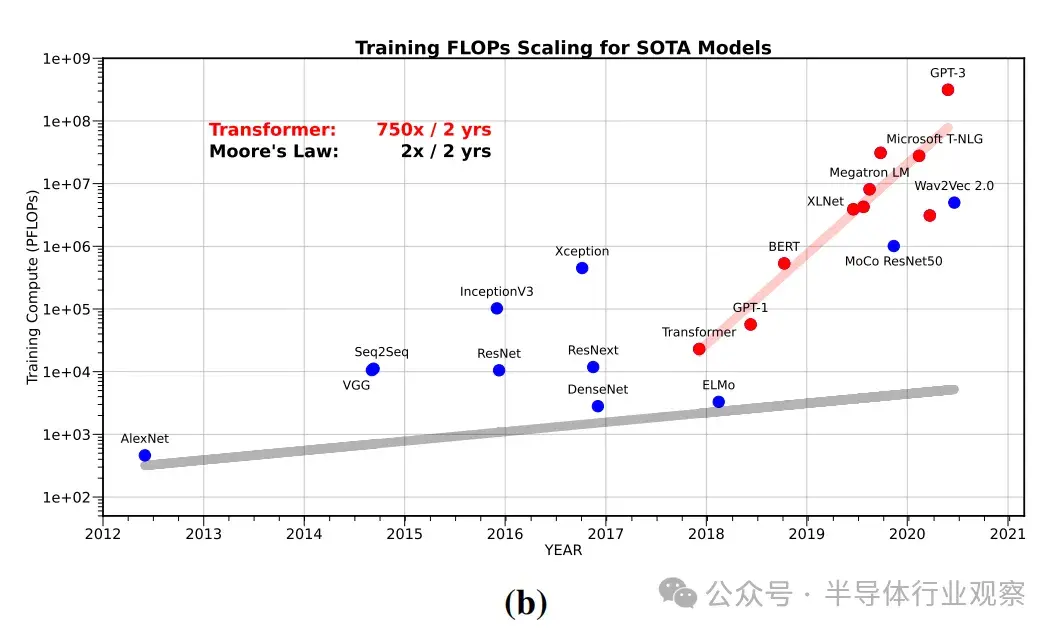
最近,訓練大型語言模型(LLM)所需的計算量以 750×/2 年的速度增長。這種指數級增長趨勢是人工智能加速器的主要驅動力,這些加速器專注於提高硬件的峯值計算能力,往往以簡化內存層次結構等其他部分為代價。
然而,這些趨勢忽略了訓練和服務人工智能模型的一個新挑戰:內存和通信瓶頸。事實上,一些人工智能應用的瓶頸正在於芯片內/芯片間(intra/inter-chip)以及人工智能加速器之間的通信,而不是計算。這並不是什麼新現象,過去就有一些著作觀察到了這一問題並提出了警告。最早的一次觀察可以追溯到 1990 年,當時 Ousterhout 在分析了影響操作系統性能的因素後得出了以下結論:
“第一個與硬件相關的問題是內存帶寬:基準測試表明,內存帶寬跟不上 CPU 的速度……"。如果未來機器的內存帶寬不能顯著提高,某些類別的應用程序可能會受到內存性能的限制”。
後來在 1995 年,威廉-伍爾夫(William Wulf )和薩莉-麥基(Sally Mckee)進一步回應了這一預測,並創造了 “內存牆 “(memory wall)一詞。他們的論證遵循一個簡單而優雅的原理。完成一個操作所需的時間取決於我們執行運算的速度,以及我們向硬件運算單元提供數據的速度。
根據這一假設,即使 80% 的數據在高速緩存中隨時可用,而只需從 DRAM 中獲取 20%,但如果從 DRAM 中獲取 20% 的高速緩存遺漏數據所需的時間超過 5 個週期,則完成運算的時間將完全受限於 DRAM。
這意味着,無論硬件每秒的運算速度有多快,問題都將完全受到 DRAM 帶寬的限制。他們預測,執行計算的速度與獲取數據的速度之間的差異將導致 “內存牆 “問題。據此,他們得出結論
“每種技術都在以指數形式不斷進步,但微處理器的指數遠遠大於 DRAM 的指數。不同指數之間的差異也呈指數增長”。
後來的一些研究也報告了類似的觀察結果。
在這項工作中,我們通過研究更近期的數據重新審視了這一趨勢,尤其關注用於訓練人工智能模型的硬件,以及用於訓練/服務這些模型的計算的特點。30 年後,上述觀察和預測再正確不過了。儘管內存技術出現了許多創新,但趨勢表明,“內存牆 “正日益成為一系列人工智能任務的主要瓶頸。
我們首先分析自 1998 年 Yann Lecun 在 MNIST 數據上訓練著名的 Lenet-5 模型以來,服務器級人工智能硬件的峯值計算量發生了怎樣的變化。我們可以看到,在過去的 20 年中,硬件的峯值計算量增長了 60,000 倍,而 DRAM 的增長為 100 倍,互連帶寬的增長為 30 倍。
內存牆問題既涉及有限的容量、內存傳輸帶寬,也涉及其延遲(比帶寬更難改善)。這需要不同層次的內存數據傳輸。例如,計算邏輯與片上內存之間的數據傳輸,或計算邏輯與 DRAM 內存之間的數據傳輸,或不同sockets上不同處理器之間的數據傳輸。在所有這些情況下,數據傳輸的容量和速度都明顯落後於硬件計算能力。
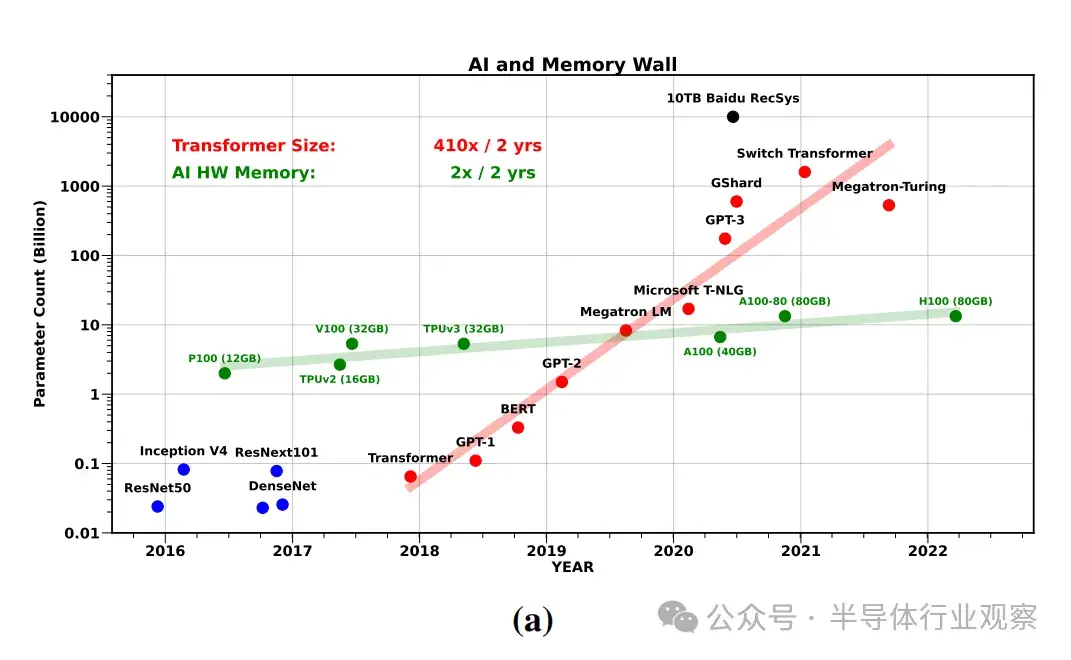
現在,如果我們研究一下最近的人工智能模型,特別是 LLM 的發展趨勢,就會發現從業人員在神經縮放定律的推動下,一直在以前所未有的水平縮放訓練最近模型所需的數據量、模型大小和計算量。儘管在 2018-2022 年的時間框架內,訓練這些最新模型所需的計算/浮點運算(FLOPs)增加了 750 倍/2 年(見圖 2),但計算並不一定是瓶頸,尤其是在模型服務方面。
首先,在這段時間內,LLM 的規模以 410×/2 年的速度增長,超過了單芯片可用的內存。我們可能希望利用分佈式內存並行性,將訓練/服務擴展到多個加速器,以避免單個硬件有限的內存容量和帶寬。然而,將工作分配給多個進程也會面臨內存牆問題:在神經網絡(NN)加速器之間移動數據的通信瓶頸,其速度和效率甚至低於片上數據移動。與單系統內存的情況類似,我們也無法克服擴展網絡帶寬的技術難題。
其次,即使模型適合單芯片,寄存器、二級緩存、全局存儲器等的片內存儲器傳輸仍日益成為瓶頸。得益於張量內核等專用計算單元的最新進展,大量計算的算術運算可以在幾個週期內完成。因此,要讓這些運算單元始終處於可用狀態,就需要快速向它們提供大量數據,而這正是芯片內存帶寬成為瓶頸的原因。
如圖 1 所示,在過去 20 年中,服務器硬件 FLOPS 的峯值以 3.0 倍/2 年的速度增長,超過了 DRAM 和互連帶寬的增長速度,而 DRAM 和互連帶寬的增長速度分別僅為 1.6 倍/2 年和 1.4 倍/2 年。這種差距使得內存而非計算日益成為瓶頸,即使是在模型可以容納在單個芯片內的情況下也是如此。
接下來,我們將對 Transformers 進行詳細的案例研究,通過分析目前常用的模型,更好地展示 FLOP、內存操作(MOP)和端到端運行時間之間的相互作用。
案例研究
在本節中,我們首先概述了與 Transformer 推理相關的運行時特性和性能瓶頸。我們研究了 Transformer 架構的兩種不同變體:編碼器(encoder)架構(如 BERT )和解碼器(decoder)架構(如 GPT ),前者可併發處理所有token,後者則在每次迭代時自動遞歸處理並生成一個token。
A. 算術強度
衡量性能瓶頸的常用方法是計算只計算變換器編碼器模型和只計算變換器解碼器模型所需的 FLOP 總數。然而,單獨使用這一指標可能會產生很大的誤導。相反,我們需要研究相關運算的算術強度。算術強度是指從內存加載的每個字節可執行的 FLOP 次數。計算方法是將 FLOP 總數除以訪問的字節總數(也稱為 MOP 或內存操作):
Arithmetic Intensity =# FLOPs/# MOPs. (1)
為了説明考慮算術深度的重要性,我們研究了 BERT-Base 和 BERT-Large ,以及 GPT-2 。前兩個是編碼器模型,其推理涉及矩陣-矩陣運算,後一個是解碼器/自動迴歸模型,其推理涉及重複矩陣-向量乘法。
B. 剖析
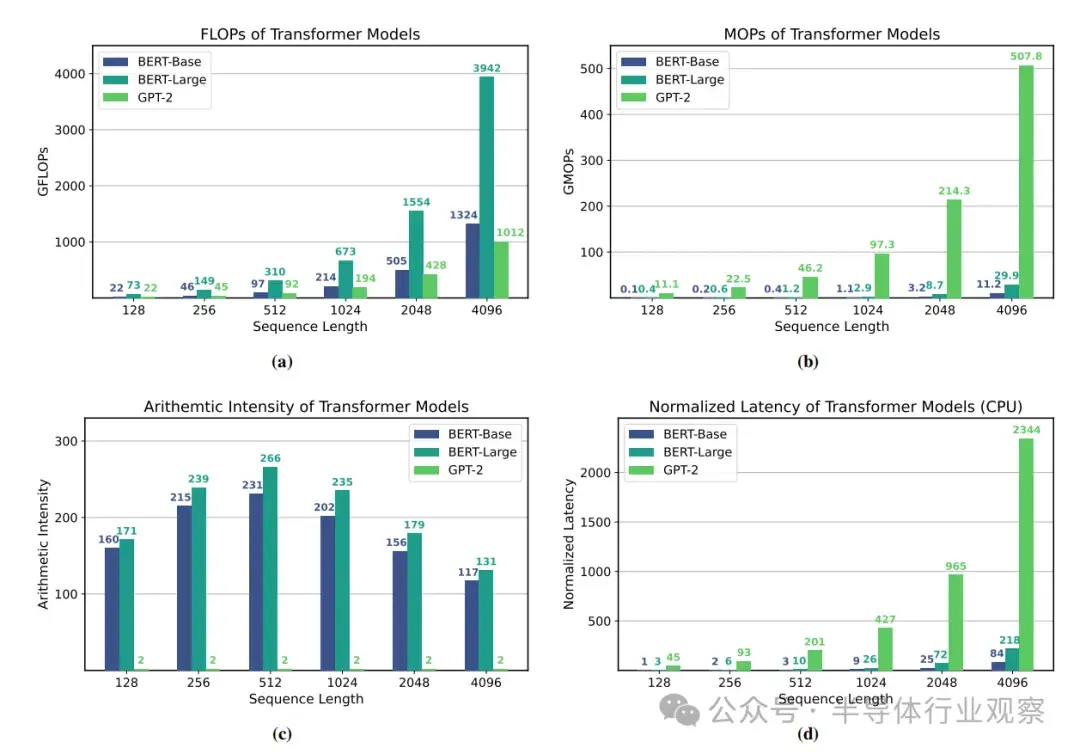
為了分析 Transformer 工作負載在商用硬件上的瓶頸,我們在英特爾 Gold 6242 CPU 上對 Transformer 推理進行了剖析。圖 3 顯示了這些模型在不同序列長度下的總 FLOPs、MOPs、算術強度和最終延遲。
很明顯,在每個序列長度下,GPT-2 的延遲都明顯長於 BERT-Base 或 BERT-Large 的延遲,儘管 BERT-Base 和 GPT-2 的模型配置和端到端 FLOPs 基本相同(如圖 3a 所示)。這是由於 GPT 的自動迴歸推理中固有的較高內存操作和較低算術強度的矩陣-向量操作(見圖 3c)。與算術強度較低的模型相比,算術強度較高的模型能以相同甚至更多的 FLOPs 運行得更快。這清楚地表明瞭內存牆是如何成為解碼器模型(在批量較小時)而不是計算的主要瓶頸的。
有望打破圍牆的解決方案
**“任何指數都不可能永遠持續下去”,**即使對於大型超標量公司來説,以 410×/2 年的速度延遲指數擴展也不會長久可行。再加上計算能力和帶寬能力之間的差距越來越大,很快就會使訓練大型模型變得非常具有挑戰性,因為成本將呈指數級增長。
為了繼續創新並打破內存牆,我們需要重新思考人工智能模型的設計,這裏有幾個問題。
首先,目前設計人工智能模型的方法大多是臨時性的,和/或涉及非常簡單的縮放規則。例如,最近的大型變形模型大多隻是最初的 BERT 模型中提出的幾乎相同的基本架構的縮放版本。
其次,我們需要設計數據效率更高的人工智能模型訓練方法。目前的 NNs 需要大量的訓練數據和數十萬次的迭代來學習,效率非常低。有些人可能會指出,這也與人類大腦的學習方式不同,人類大腦通常只需要為每個概念/類別提供很少的示例。
目前的優化和訓練方法需要進行大量的超參數調整(如學習率、動量等),這往往需要進行數百次的試錯才能找到正確的參數設置,從而成功訓練出一個模型。因此,圖 2 (b) 中報告的訓練成本只是實際開銷的下限,真正的成本通常要高得多。
最先進模型的規模過大,使得部署這些模型進行推理非常具有挑戰性。這不僅限於 GPT-3 等模型。事實上,部署超標量公司使用的大型推薦系統也是一大挑戰。
最後,硬件加速器的設計主要集中在提高峯值計算能力上,對改善內存約束工作負載的關注相對較少。這使得訓練大型模型和探索其他模型(如圖網絡)變得困難,而圖網絡通常受帶寬限制,無法有效利用當前的加速器。
所有這些問題都是機器學習中的基本問題。在此,我們將簡要討論針對上述三個問題的最新研究(包括我們自己的一些研究)。
A. 高效訓練算法
訓練 NN 模型的主要挑戰之一是需要對超參數進行強制調整(brute-force hyperparameter tuning)。這包括尋找學習率(finding the learning rate)、退火時間表(annealing schedule)、收斂所需的迭代次數(iterations needed to converge)等。這為訓練 SOTA 模型增加了開銷。其中許多問題都是由用於訓練的一階 SGD 方法引起的。
雖然 SGD 變體很容易實現,但它們對超參數的調整並不穩健,而且很難調整新模型,因為對於新模型來説,正確的超參數集是未知的。解決這個問題的一個可行方法是使用二階隨機優化方法[43]。這些方法通常對超參數調整更加穩健,而且可以實現 SOTA 。
不過,目前的方法佔用的內存要高出 3-4 倍。在這方面,微軟的 Zero 框架是一個很有前途的研究方向,該框架展示瞭如何通過移除/分隔冗餘優化狀態變量,在相同內存容量下訓練出 8 倍更大的模型。如果能解決這些高階方法的開銷問題,就能大大降低訓練大型模型的總成本。
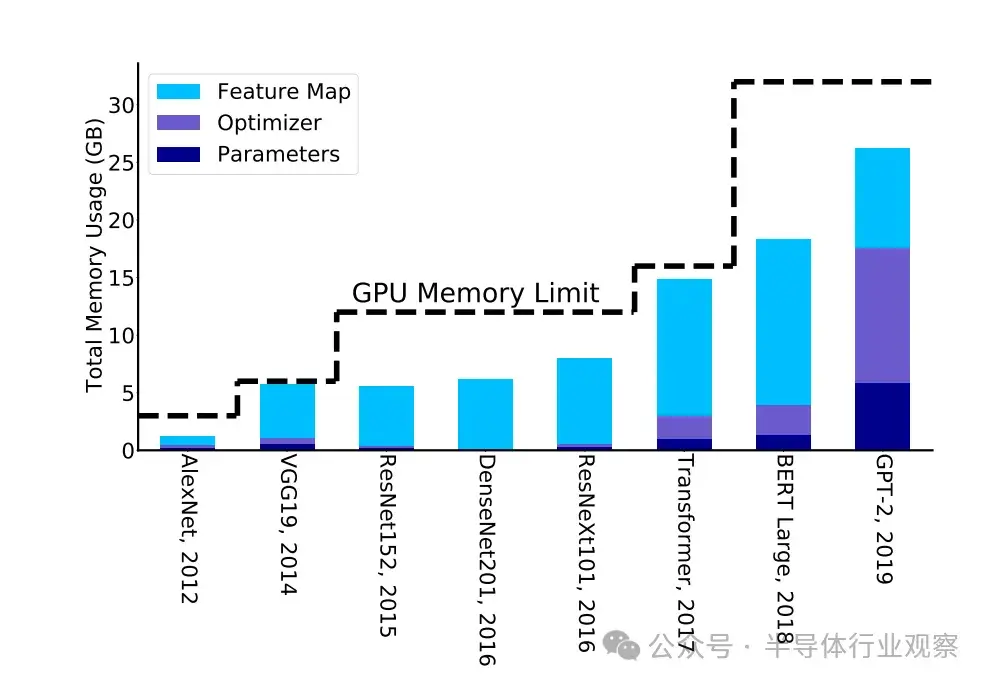
另一種有前途的方法包括減少內存佔用和提高優化算法的數據局部性,但代價是執行更多的計算。數值線性代數中一個顯著的例子是避免通信算法系列。優化 NN 訓練內存的一個例子是再物化,即在前向傳遞過程中,我們只存儲/檢查點激活的一個子集,而不是保存所有激活。這就減少了特徵圖的內存佔用,如圖 4 所示。在需要時,可以重新計算其餘的激活點。儘管這會增加計算量,但只需增加 20% 的計算量,就能將內存佔用大幅減少 5 倍。這還能讓從業人員在單芯片內存上訓練大型模型,而不是利用分佈式訓練,因為分佈式訓練通常難以設置(主要的超級分頻器公司除外),而且難以調試(對於非專業開發人員而言)。
有趣的是,傳統趨勢表明,新的 NN 模型架構是根據研究人員在單芯片內的訪問權限而開發的,而不是使用複雜的分佈式內存方法(見圖 4)。當然,有很多反例來自大型超級計算公司,它們有專門的團隊支持研究人員部署大型模型,但如果我們考慮整個社區,這樣的例子就很有限了。事實上,即使是最近的 LLM,也經常要花費大量精力來壓縮模型,使其適合在系統中使用,以便讓更多的研究人員可以訪問模型。
另一個重要的解決方案是設計對低精度訓練具有魯棒性的優化算法。事實上,人工智能加速器的重大突破之一就是使用半精度(FP16)算術,而不是單精度。這使得硬件計算能力提高了 10 倍以上。然而,利用當前的優化方法,在不降低精度的情況下進一步降低精度(從半精度降低到 INT8)一直是個難題。最近一個很有前途的趨勢是混合使用 FP8 和 FP16(甚至最近的 FP4)。這一領域的算法創新肯定能讓我們更有效地利用硬件,並能讓芯片的更多區域用於改善內存(這通常被稱為內存空隙懲罰)。
B. 高效部署
部署最近的 SOTA 模型如 GPT-3 [3])或大型推薦系統相當具有挑戰性,因為它們需要分佈式內存部署來進行推理。解決這個問題的一個可行辦法是壓縮這些模型,通過降低精度(即量化)、刪除(即剪枝)冗餘參數或設計小語言模型來進行推理。
第一種方法,即量化,可以在訓練和/或推理步驟中應用。雖然將訓練精度降低到 FP16 以下非常具有挑戰性,但在推理中使用超低精度是可能的。利用當前的方法,將推理量化到 INT4 精度相對容易,對精度的影響也很小。這使得模型足跡和延遲減少了 8 倍。然而,亞 INT4 精度的推理更具挑戰性,目前是一個非常活躍的研究領域。
第二種方法是剪枝,即完全刪除/剪除模型中的冗餘參數。利用目前的方法,可以在結構稀疏的情況下剪除多達 30% 的神經元,在非結構稀疏的情況下剪除多達 80% 的神經元,而對精度的影響微乎其微。然而,突破這一限制是非常具有挑戰性的,而且往往會導致致命的精度下降。解決這個問題還是一個未決難題。
第三種方法,即小語言模型,可以開闢全新的領域,使人工智能得到廣泛應用。有趣的是,自 2017 年推出 Transformer 模型以來,用於 LLM 的模型一直沒有改變。迄今為止,行之有效的方法是擴大模型的數據和規模,這導致了這些模型的 “新興能力”。不過,最近關於小型語言模型的工作已在其能力方面取得了可喜的成果。如果模型能完全貼合芯片,那麼就能實現數量級的提速和節能。
C. 反思人工智能加速器的設計
同時提高芯片的內存帶寬和峯值計算能力面臨着根本性的挑戰。不過,犧牲峯值計算能力來實現更好的計算/帶寬權衡是有可能的。事實上,CPU 架構已經包含了優化的高速緩存層次結構。這就是為什麼在處理帶寬受限問題時,CPU 的性能比 GPU 好得多。這類問題包括大型推薦問題。
然而,當今 CPU 面臨的主要挑戰是,其峯值計算能力(即 FLOPS)比 GPU 或 TPU 等人工智能加速器低一個數量級。其中一個原因是,人工智能加速器的設計主要是為了達到最大峯值計算能力。這通常需要移除緩存層次結構等組件,以增加更多的計算邏輯。我們可以設想一種介於這兩個極端之間的替代架構,最好是採用更高效的高速緩存,更重要的是採用容量更大的 DRAM(可能是帶寬不同的 DRAM 層次結構)。後者可以有效緩解分佈式內存通信瓶頸。
結論
在 NLP 中,訓練最新 SOTA Trans former 模型的計算成本以 750×/2yrs 的速度遞增,模型參數大小以 410×/2yrs 的速度遞增。相比之下,硬件 FLOPS 峯值的擴展速度為 3.0×/2yrs,而 DRAM 和互連帶寬的擴展速度分別為 1.6×/2yrs 和 1.4×/2yrs,越來越落後。
從這個角度來看,硬件 FLOPS 的峯值在過去 20 年中增長了 60,000 倍,而 DRAM/互連帶寬在同期僅分別增長了 100 倍/30 倍。
在這種趨勢下,內存(尤其是芯片內/芯片間內存傳輸)將很快成為服務大型人工智能模型的主要限制因素。因此,我們需要重新思考人工智能模型的訓練、部署和設計,以及如何設計人工智能硬件來應對這堵日益嚴峻的內存牆。
致謝本文作者:Amir Gholami,Zhewei Yao, Sehoon Kim,Coleman Hooper, Michael W. Mahoney,Kurt Keutzer,University of California, Berkeley,ICSI,LBNL
參考鏈接
[1] G. Ballard, J. Demmel, O. Holtz, and O. Schwartz, “Minimizing communication in numerical linear alge bra,” SIAM Journal on Matrix Analysis and Applications, vol. 32, no. 3, pp. 866–901, 2011.
[2] L. Bottou, F. E. Curtis, and J. Nocedal, “Optimization methods for large-scale machine learning,” SIAM Review, vol. 60, no. 2, pp. 223–311, 2018.
[3] T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Ka plan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell et al., “Language models are few-shot learn ers,” Advances in neural information processing systems, vol. 33, pp. 1877–1901, 2020.
[4] A. Chowdhery, S. Narang, J. Devlin, M. Bosma, G. Mishra, A. Roberts, P. Barham, H. W. Chung, C. Sutton, S. Gehrmann et al., “Palm: Scaling language modeling with pathways,” Journal of Machine Learning Research, vol. 24, no. 240, pp. 1–113, 2023.
[5] H. W. Chung, L. Hou, S. Longpre, B. Zoph, Y. Tay, W. Fedus, Y. Li, X. Wang, M. Dehghani, S. Brahma et al.,
“Scaling instruction-finetuned language models,” arXiv preprint arXiv:2210.11416, 2022.
[6] T. Dettmers, R. Svirschevski, V. Egiazarian, D. Kuznedelev, E. Frantar, S. Ashkboos, A. Borzunov, T. Hoefler, and D. Alistarh, “Spqr: A sparse-quantized representation for near-lossless llm weight compression,” arXiv preprint arXiv:2306.03078, 2023.
[7] J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova, “BERT: Pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Asso ciation for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), 2019, pp. 4171–4186.
[8] E. Frantar and D. Alistarh, “Sparsegpt: Massive language models can be accurately pruned in one-shot,” 2023.
[9] E. Frantar, S. Ashkboos, T. Hoefler, and D. Alistarh,
“OPTQ: Accurate quantization for generative pre-trained transformers,” in The Eleventh International Conference on Learning Representations, 2023.
[10] A. Gholami, S. Kim, Z. Dong, Z. Yao, M. W. Mahoney, and K. Keutzer, “A survey of quantization methods for efficient neural network inference,” in Low-Power Computer Vision. Chapman and Hall/CRC, 2022, pp. 291–326.
[11] B. Ginsburg, S. Nikolaev, A. Kiswani, H. Wu, A. Gho laminejad, S. Kierat, M. Houston, and A. Fit-Florea, “Tensor processing using low precision format,” Dec. 28 2017, uS Patent App. 15/624,577.
[12] J. L. Hennessy and D. A. Patterson, Computer architec ture: a quantitative approach. Elsevier, 2011.
[13] T. Hoefler, D. Alistarh, T. Ben-Nun, N. Dryden, and A. Peste, “Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks,” The Journal of Machine Learning Research, vol. 22, no. 1, pp. 10 882–11 005, 2021.
[14] J. Hoffmann, S. Borgeaud, A. Mensch, E. Buchatskaya, T. Cai, E. Rutherford, D. de Las Casas, L. A. Hendricks, J. Welbl, A. Clark, T. Hennigan, E. Noland, K. Millican, G. van den Driessche, B. Damoc, A. Guy, S. Osin dero, K. Simonyan, E. Elsen, O. Vinyals, J. Rae, and L. Sifre, “An empirical analysis of compute-optimal large language model training,” in Advances in Neural Infor mation Processing Systems, vol. 35, 2022, pp. 30 016– 30 030.
[15] P. Jain, A. Jain, A. Nrusimha, A. Gholami, P. Abbeel, J. Gonzalez, K. Keutzer, and I. Stoica, “Checkmate: Breaking the memory wall with optimal tensor remate rialization,” Proceedings of Machine Learning and Sys tems, vol. 2, pp. 497–511, 2020.
[16] A. Q. Jiang, A. Sablayrolles, A. Mensch, C. Bamford, D. S. Chaplot, D. d. l. Casas, F. Bressand, G. Lengyel, G. Lample, L. Saulnier et al., “Mistral 7b,” arXiv preprint arXiv:2310.06825, 2023.
[17] S. Kim, C. Hooper, A. Gholami, Z. Dong, X. Li, S. Shen, M. W. Mahoney, and K. Keutzer, “Squeezellm: Dense-and-sparse quantization,” arXiv preprint arXiv:2306.07629, 2023.
[18] S. Kim, C. Hooper, T. Wattanawong, M. Kang, R. Yan, H. Genc, G. Dinh, Q. Huang, K. Keutzer, M. W. Ma honey, Y. S. Shao, and A. Gholami, “Full stack optimiza tion of transformer inference: a survey,” Workshop on Architecture and System Support for Transformer Models (ASSYST) at ISCA, 2023.
[19] V. A. Korthikanti, J. Casper, S. Lym, L. McAfee, M. Andersch, M. Shoeybi, and B. Catanzaro, “Reducing activation recomputation in large transformer models,” Proceedings of Machine Learning and Systems, vol. 5, 2023.
[20] S. Krishna and R. Krishna, “Accelerating recom mender systems via hardware scale-in,” arXiv preprint arXiv:2009.05230, 2020.
[21] W. Kwon, S. Kim, M. W. Mahoney, J. Hassoun, K. Keutzer, and A. Gholami, “A fast post-training prun ing framework for transformers,” in Advances in Neural Information Processing Systems, vol. 35. Curran Asso ciates, Inc., 2022, pp. 24 101–24 116.
[22] Y. LeCun, L. Bottou, Y. Bengio, P. Haffner et al., “Gradient-based learning applied to document recogni tion,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278– 2324, 1998.
[23] J. Lin, J. Tang, H. Tang, S. Yang, X. Dang, C. Gan, and S. Han, “Awq: Activation-aware weight quantization for llm compression and acceleration,” 2023.
[24] J. McCalpin, “Stream: Sustainable memory bandwidth in high performance computers,” http://www. cs. virginia. edu/stream/, 2006.
[25] S. A. McKee, “Reflections on the memory wall,” in Pro ceedings of the 1st Conference on Computing Frontiers, ser. CF ’04. New York, NY, USA: Association for Computing Machinery, 2004, p. 162.
[26] P. Micikevicius, S. Narang, J. Alben, G. Diamos, E. Elsen, D. Garcia, B. Ginsburg, M. Houston, O. Kuchaiev, G. Venkatesh, and H. Wu, “Mixed preci sion training,” in International Conference on Learning Representations, 2018.
[27] P. Micikevicius, D. Stosic, N. Burgess, M. Cornea, P. Dubey, R. Grisenthwaite, S. Ha, A. Heinecke, P. Judd, J. Kamalu et al., “Fp8 formats for deep learning,” arXiv preprint arXiv:2209.05433, 2022.
[28] G. Moore, “No exponential is forever: but ”forever” can be delayed! [semiconductor industry],” in 2003 IEEE In ternational Solid-State Circuits Conference, 2003. Digest of Technical Papers. ISSCC., 2003, pp. 20–23 vol.1.
[29] M. Naumov, D. Mudigere, H.-J. M. Shi, J. Huang, N. Sundaraman, J. Park, X. Wang, U. Gupta, C.-J. Wu, A. G. Azzolini et al., “Deep learning recommendation model for personalization and recommendation systems,” arXiv preprint arXiv:1906.00091, 2019.
[30] J. Ousterhout, “Why aren’t operating systems getting faster as fast as hardware?” in USENIX Summer Con ference, 1990, 1990.
[31] D. Patterson, T. Anderson, N. Cardwell, R. Fromm, K. Keeton, C. Kozyrakis, R. Thomas, and K. Yelick, “A case for intelligent ram,” IEEE micro, vol. 17, no. 2, pp. 34–44, 1997.
[32] D. A. Patterson, “Latency lags bandwith,” Communica tions of the ACM, vol. 47, no. 10, pp. 71–75, 2004.
[33] A. Radford, J. Wu, R. Child, D. Luan, D. Amodei,
and I. Sutskever, “Language models are unsupervised multitask learners,” OpenAI blog, vol. 1, no. 8, p. 9, 2019.
[34] S. Rajbhandari, J. Rasley, O. Ruwase, and Y. He, “Zero: Memory optimizations toward training trillion parameter models,” in SC20: International Conference for High Performance Computing, Networking, Storage and Anal ysis. IEEE, 2020, pp. 1–16.
[35] T. Schick and H. Schutze, “It’s not just size that matters: ¨ Small language models are also few-shot learners,” arXiv preprint arXiv:2009.07118, 2020.
[36] D. Sites, “It’s the memory, stupid!” Microprocessor Re port, pp. 18–24, 1996.
[37] H. Touvron, L. Martin, K. Stone, P. Albert, A. Almahairi, Y. Babaei, N. Bashlykov, S. Batra, P. Bhargava, S. Bhos ale et al., “Llama 2: Open foundation and fine-tuned chat models,” arXiv preprint arXiv:2307.09288, 2023.
[38] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” in Advances in neural infor mation processing systems, 2017, pp. 5998–6008.
[39] J. Wei, Y. Tay, R. Bommasani, C. Raffel, B. Zoph, S. Borgeaud, D. Yogatama, M. Bosma, D. Zhou, D. Met zler et al., “Emergent abilities of large language models,” arXiv preprint arXiv:2206.07682, 2022.
[40] M. V. Wilkes, “The memory wall and the cmos end point,” ACM SIGARCH Computer Architecture News, vol. 23, no. 4, pp. 4–6, 1995.
[41] S. Williams, A. Waterman, and D. Patterson, “Roofline: an insightful visual performance model for multicore architectures,” Communications of the ACM, vol. 52, no. 4, pp. 65–76, 2009.
[42] W. A. Wulf and S. A. McKee, “Hitting the memory wall: Implications of the obvious,” ACM SIGARCH computer architecture news, vol. 23, no. 1, pp. 20–24, 1995.
[43] Z. Yao, A. Gholami, S. Shen, M. Mustafa, K. Keutzer, and M. Mahoney, “Adahessian: An adaptive second order optimizer for machine learning,” in proceedings of the AAAI conference on artificial intelligence, vol. 35, no. 12, 2021, pp. 10 665–10 673.
[44] Z. Yao, R. Yazdani Aminabadi, M. Zhang, X. Wu, C. Li, and Y. He, “Zeroquant: Efficient and affordable post-training quantization for large-scale transformers,” in Advances in Neural Information Processing Systems, S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh, Eds., vol. 35. Curran Associates, Inc., 2022, pp. 27 168–27 183.