寫給程序員的可逆計算理論辨析補遺_風聞
canonical-云计算实现计算的云化,可逆计算实现计算的可逆化33分钟前
可逆計算理論是作者試圖從物理學的基本原理出發來解釋軟件開發實踐的時候所發現的一種面向演化的軟件構造理論,所以它的方法論來源不是計算機科學本身,而是理論物理學,它所描述的是一種程序員不太熟悉的、相對抽象的軟件構造規律。我在可逆計算理論的方法論來源一文中初步介紹了理論物理學和數學所帶來的啓發性思想。最近,我又專門寫了一篇文章寫給程序員的可逆計算理論辨析,從程序員熟悉的概念出發詳細解釋了差量與差量合併在程序實踐中的具體形式和做法。根據讀者的反饋信息,在本文中我將繼續補充一些針對可逆計算理論的概念辨析,澄清對於可逆計算理論的一些常見誤解。
一. 函數(業務處理邏輯)如何實現差量化
差量是定義在支持某種差量合併運算的模型空間中的變化量,不同的模型空間具有不同的差量形式。這意味着對於同一個實體,如果放到不同的模型空間中去觀察,我們實際上會得到不同的結果。
首先,所有的結構都可以在通用的二進制比特空間中得到表示,比如函數A存儲在文件中時對應於二進制數據10111…,而我們希望將它轉換為函數B,它對應的二進制表示為010010…。在抽象的數學層面,尋找將函數A變換為函數B的差量X,相當於是求解如下方程 A⊕X=B。很顯然,如果將⊕定義為二進制比特層面的異或操作,則我們可以自動求解得到 X=A⊕B。
A ⊕ B = A ⊕ (A ⊕ X) = (A ⊕ A) ⊕ X = 0 ⊕ X = X
在證明中我們用到了異或操作的歸零律、結合律和恆等律。
雖然在二進制比特空間中我們總是可以求解得到函數的差量,但是這個差量卻沒有什麼業務價值(對於二進制級別的壓縮軟件等還是有價值的)。我們既不能直觀的理解它,也缺少便利的手段來直觀的操縱它。
第二個常用的表示空間是源代碼所在的行文本空間:所有的源碼文件都可以通過代碼行來描述。我們可以相對直觀的在這個空間中定義代碼的差量並很方便的操縱它。比如説一般的IDE工具都提供了拷貝行、刪除行、複製行的操作快捷鍵。更進一步,所有調試工具和版本管理工具的業務價值都建立在行文本空間之上。例如,源代碼版本管理工具在比較不同版本之間的差異時,會自動計算得到行文本空間中的Diff表示,而經過訓練的程序員在代碼評審時可以直接理解Diff表示。但是,行文本空間是一個與具體業務領域無關的通用表示空間,這導致它在描述業務邏輯代碼的時候缺乏穩定性。一些在業務層面完全等價的結構變換會產生文本行空間中的大量差異。例如,代碼格式化之後可能導致文本行層面出現巨大差異。此外調整函數的定義順序一般並不影響程序語義,但是從行文本空間的角度來看,卻是天翻地覆的巨大變化。
Go語言在編譯的時候總是按照固定的格式化規則對源碼進行格式化。表面上看起來,這一做法使得程序員喪失了對源碼的格式控制,但有趣的是,它並不意味着某種功能缺失,反而成就了更加穩定的文本行差量化表示形式。
為了得到一種穩定的、具有明確業務語義的函數差量化表示形式,我們必須要在領域專用的模型空間中實現對函數的定義。具體來説,我們可以將函數分解為多個步驟,然後為每個步驟分配一個唯一id等等。在Nop平台中,我們定義了兩種可以實現分佈式異步調用函數的差量化邏輯表達形式。
1. 基於堆棧結構的TaskFlow。每一個步驟執行完畢之後缺省會自動執行下一個兄弟節點,而當所有的子節點都執行完畢之後會返回父節點繼續執行。在運行時,可以按照父子節點關係查找到每個節點當前持有的狀態數據,相當於是構成一個堆棧空間。通過引入外部持久化存儲,TaskFlow可以實現類似程序語言中的Continuation機制:即某個步驟執行時可以將整個流程或者流程的一個分支掛起,然後外部程序可以調用TaskFlow的continueWith函數,從掛起的步驟繼續執行。TaskFlow的XDef元模型參見task.xdef
2. 基於圖結構的Workflow。工作流模型可以描述大數據處理領域常見的DAG有向無環圖,也可以描述辦公自動化領域帶回退、循環功能的審批流程圖。工作流完全依賴於to-next步驟遷移規則來指定下一個待執行的步驟。同時,因為工作流的步驟之間完全平級,沒有嵌套關係(子流程除外),所以在流程掛起之後,可以從任意一個步驟重新開始執行,在Workflow中實現Continuation機制要更加簡單。Workflow的XDef元模型參見wf.xdef
<task x:extends=“send-order.task.xml”> <steps> <step id=“save-order” /> <step id=“send-email”> … </step> </steps> </task>
以上定義表示,對send-order.task.xml這個任務定義進行差量化調整,在save-order這一步驟之後增加一個send-email步驟。我們也可以通過差量化形式來調整某個步驟的配置參數或者刪除某個步驟等。
二. 可逆計算能否應用於運行時演化
我在此前的文章中多次強調了可逆計算可以通過編譯期元編程機制來實現,有些同學可能會產生疑問,這是否意味着可逆計算所描述的只是靜態的系統演化實踐(編譯期實施差量),那動態的系統演化(運行期實施差量)是否也能納入可逆計算理論的描述範圍?
這是一個非常有趣的問題。先説一下結論: 可以,可逆計算可以應用於運行期演化。
首先,在運行期我們可以使用延遲編譯和即時編譯技術。在Nop平台中,如果系統上線之後我們修改了DSL模型文件,則所有依賴於這個DSL模型的相關模型都會自動失效,下次再訪問到這些模型的時候會自動重新加載編譯。比如説,修改了NopAuthUser.xmeta文件會導致NopAuthUser.view.xml和用到NopAuthUser.view.xml的所有頁面模型也會自動更新。DSL模型的自動更新過程不需要重新啓動系統,只是更新緩存中的編譯結果。
SAAS多租户系統在抽象的層面上看,也可以理解為一個Delta定製問題。每個租户對應於一個Delta,而且這些Delta在運行時的狀態空間也是相互隔離的。實際上,因為Nop平台系統化的考慮了Delta的構建、分解機制,相比於其他技術方案它能夠更加優雅的處理運行期演化問題。基於Nop平台的設計模式,我們可以在完全不停機的情況下實現持續的軟件演化。
運行期的解釋模型和編譯期的代碼生成模型之間的區別可以通過函數式編程中的Curry化機制來理解。例如,低代碼前端框架AMIS的執行模型對應於 renderAmis(pageJson, pageData)。如果進行Curry化,則它對應於 (renderAmis(pageJson))(pageData)。如果我們可以對renderAmis(pageJson)這一形式中包含的邏輯進行優化,就相當於是執行 Component = CodeGenerator(pageJson),編譯過程等價於通過某種代碼生成器生成優化後的代碼,在編譯期就可以提前執行大量的判斷和循環邏輯,而在運行期就只需要保留必要的Component(pageData)邏輯即可。
更為複雜的一個問題是運行期的狀態空間是否也能納入Delta****的管理範圍,畢竟整個應用系統的完整描述 = 結構 + 狀態。答案同樣是可以,因為可逆計算是一個完全抽象的理論,它可以將結構空間+狀態空間綜合在一起,定義一個完整的高維空間,然後再考慮這個高維空間中的差量化演化。(在物理學中,這個高維空間被稱為相空間)。但是從實踐的角度上説,考慮狀態將導致需要處理的複雜度直線上升,所以一般情況下我們只會考慮結構空間中的Delta,而忽略狀態空間。
具體舉一個例子,比如説我們現在要對一個機器人進行Delta改進。對這個機器人的完整描述肯定是包括它的結構以及這些結構所處的狀態,比如説機器人處於高速的運動狀態中,我們需要描述它的各個部分的相對速度、加速度、角速度,甚至壓力、温度等,但是一般情況下我們並不會在機器人的工作模式下對它進行改裝,而是要把它轉入到靜息模式,也就是某種非激活的模式。工作模式下的各種狀態信息對於改裝而言是不相關的、可忽略的。少數極端的情況下,我們需要在行駛的火車上換車輪,那麼基本的做法大概是: 先使用時間靜止技術,在局部凍結時間線,然後將部分需要保持的狀態序列化到存儲中,然後修改結構,再次加載狀態,一切就緒後再恢復時間演化。在Delta修正所應用的過程中,時間是靜止的,各類狀態是凍結的,狀態本身也是可以進行Delta****修正的數據。(比如説我們使用了某種鎖機制,直接阻止外部操作,從外部使用者來看系統不再執行後續步驟,等價於時間靜止。更復雜的技術則涉及到多重宇宙:在某個時刻通過快照複製分裂為多重宇宙之後,需要在平行宇宙中不斷複製Delta進行追賬,直到對齊到某個時間點,然後在短時間內靜止時間,完成時間線切換)
關於時間靜止的一個有趣應用,可以參見我的文章 Paxos的魔法學研究報告
對狀態進行Delta修正的複雜度在於對象關聯的狀態信息並不是僅僅由對象自身所決定。比如我們的機器人正在和別的機器人進行激烈的對戰,它的狀態本質上是與對手相互作用導致的結果。如果需要復現這個狀態,必須要考慮到能量守恆、動量守恆、角動量守恆等一系列物理約束。我們無法單方面的從機器人個體的角度出發復現它的狀態,而是必須要考慮所有與它交互的客體的情況,需要考慮環境與機器人之間的相互影響,這導致復現狀態或者修改狀態是一件非常複雜的事情。如果我們通過Delta定製修改了對象結構,那麼如何調整運行期的狀態數據,使得它與新的對象結構以及外部運行時環境相協調就成為一件非常棘手的事情。
根據上面的討論,如果我們希望在運行期實現演化,基本的做法有兩種:
1. 分離結構和狀態,比如微服務強調無狀態設計,將業務狀態保留在共享存儲中,所以可以隨時啓停
2. 定義激活和非激活兩種模式,切換到非激活模式下完成結構修訂。
如果發散一下考慮生物界的演化問題。 我們可以把DNA看作是某種承載信息的DSL,生物的成長過程對應於Generator,它根據DSL的信息結合環境信息塑造出生物的本體。同時生物在應對具體問題挑戰的時候,還可以利用外部的各種Delta。比如人可以穿上潛水服這個Delta,獲得在水中活動的能力,可以加上不同厚度的衣服,獲得在極寒和極熱地區活動的能力。而一般的動植物能夠加裝的Delta很少,而特化的物理器官在增加某種適應性的同時也削弱了在其他環境中的適應性。比如北極熊的毛皮很保暖,很適合在寒冷的北極生活,這也導致了它無法適應熱帶的氣候。
三. 現有系統要做到差量化是不是要推倒重建
Nop平台的代碼看起來有點多(現在大概有二十多萬行Java代碼,包括十萬行左右自動生成的代碼),有些程序員看到之後可能感到有點疑慮,引入可逆計算的差量化計算模式,是否意味着必須要使用Nop平台?而使用Nop平台是否意味着要重寫原有的業務代碼?
首先,Nop平台的代碼顯得比較多是因為它沒有直接使用Spring,而是重寫了Java生態中的大量的底層框架,在重寫的過程中納入了很多創新的設計,提升了應用層的易用性,也提升了系統的性能。
為什麼重寫底層框架
目前流行的底層框架其設計時間都比較久遠,歷史積累的實現代碼已經非常臃腫,因此面對新的技術環境挑戰,例如異步化、支持GraalVM原生編譯、支持GraphQL編程模型等,存在着船大難掉頭的難題。以Hibernate為例,它具有至少30****萬行以上的代碼量,卻長期存在着不支持在From子句中使用子查詢,不支持關聯屬性之外的表連接、難以優化延遲屬性加載等問題。NopORM引擎實現了Hibernate+MyBatis的所有核心功能,可以使用大多數SQL關聯語法,支持With子句、Limit子句等,同時增加了邏輯刪除、多租户、分庫分表、字段加解密、字段修改歷史跟蹤等應用層常用的功能,支持異步調用模式,支持類似GraphQL的批量加載優化,支持根據Excel模型直接生成GraphQL服務等。實現所有這些功能,NopORM中手寫的有效代碼量只有1****萬行左右。類似的,在Nop平台中我們通過4000行左右的代碼實現了支持條件裝配的NopIoC容器,通過3000行左右的代碼實現了支持灰度發佈的分佈式RPC框架,通過3000代碼實現了採用Excel作為設計器的中國式報表引擎NopReport等。具體介紹參見以下文章:
• 採用Excel作為設計器的開源中國式報表引擎:NopReport
之所以重寫這些框架只需要很少的代碼量,一個很重要的原因在於它們共用了Nop平台的很多通用機制。任何一個具有一定複雜度的底層框架在某種意義上説都是提供了一種DSL領域特定語言,比如Hibernate的hbm模型文件,Spring的beans.xml對象定義文件,Report的報表模型文件,RPC所使用的接口定義文件等。Nop平台為開發自定義的DSL提供了一系列的技術支撐,避免了每個框架都自行去實現模型的解析、加載、轉換功能。同時,Nop平台提供了高度可定製的表達式語言和模板語言引擎,也避免了每個框架都重新去實現類似的腳本引擎。還有一點是,每個框架都使用IoC容器來實現動態裝配,避免了自行去實現插件擴展機制。
Nop平台統一了所有底層框架所使用的DSL描述方式,因此可以使用統一的XDef元模型定義語言來定義不同的DSL,這使得我們可以提供統一的IDE插件來實現對不同DSL的編程支持,可以實現多個DSL之間的無縫嵌入。在未來,我們還將提供統一的可視化設計器生成器,它根據XDef元模型自動為DSL****生成可視化設計工具。藉助於XDSL內置的Delta差量定製機制,我們可以實現在完全不修改基礎產品源碼的情況下,實現深度的定製化開發。具體介紹參見文章:
如果不重寫底層框架,如何引入差量化機制
Nop平台重寫底層框架只是為了簡化編程、提升性能。如果堅持使用傳統的開源框架,同樣可以引入差量化機制,只是使用起來沒有那麼方便。實際上,在JSON格式基礎上實現差量化虛擬文件系統和Delta差量合併算法大概只需要幾千行代碼。
如果希望以最小的成本向系統中引入可逆計算,可以使用如下兩種方式:
1. 將Nop平台作為增量式代碼生成器
Nop平台的代碼生成器可以集成在Maven打包工具中使用,在執行mvn package指令的時候會自動運行precompile和postcompile目錄下的所有代碼生成腳本。生成的代碼可以脱離Nop平台運行,完全不需要改變原有的運行模式,也不會增加新的運行時依賴。
Nop平台支持程序員定義自己的領域模型,也支持擴展平台內置的數據模型、API模型等,而且這種擴展都是通過Delta定製方式實現,增加模型屬性時不需要修改Nop平台的代碼。目前已經有人使用Nop平台的代碼生成器來生成其他低代碼平台所需的模型文件。
Nop平台的代碼生成器採用了一系列創新的設計,它的實現方式和完成的功能與常見的代碼生成腳手架有着本質性區別,具體介紹參見文章 數據驅動的差量化代碼生成器
除了集成在maven工具中使用之外,我們有可以使用命令行方式來執行持續性的代碼生成。
java -jar nop-cli.jar run tasks/gen-web.xrun -t=1000
<!-- gen-web.xrun --> <c:script><![CDATA[ import io.nop.core.resource.component.ResourceComponentManager; import io.nop.core.resource.VirtualFileSystem; import io.nop.codegen.XCodeGenerator; import io.nop.xlang.xmeta.SchemaLoader; import io.nop.commons.util.FileHelper; assign(“metaDir”,"/meta/test"); let path = FileHelper.getRelativeFileUrl("./target/gen"); let codegen = new XCodeGenerator(’/nop/test/meta-web’,path); codegen = codegen.withDependsCache(); codegen.execute("/",$scope); ]]></c:script>
上面的例子表示每隔1秒鐘執行一次gen-web.xrun任務,而這個任務的具體內容是針對/meta/test虛擬路徑下的所有meta文件,應用/nop/test/meta-web虛擬路徑下的代碼生成模板,生成的代碼保存到target/gen目錄下。代碼生成器設置了withDependsCache,因此每次執行的時候它都會檢查代碼生成器所用到的模型文件是否已經發生變化,只有發生變化的時候才會重新生成,否則會直接跳過。例如,如果my.page.json文件是根據NopAuthUser.xmeta模型以及web.xlib這個控件庫生成的,那麼只有當NopAuthUser.xmeta文件或者web.xlib文件發生變化的時候,才會重新生成my.page.json。
這種依賴追蹤機制有些類似於前端Vite打包工具所內置的修改監聽功能:當發現源碼發生改變的時候自動重新加載源碼,並把修改推送到前端瀏覽器中。
2. 使用Nop平台的統一模型裝載器
Nop平台所提供的Delta定製機制主要是用於動態生成並組裝各類模型文件,並不涉及到任何運行時框架方面的知識,因此它可以很自然的與任何設計良好的運行時框架進行對接。具體的對接策略就是將原先加載模型文件的函數調用替換為對Nop平台中的統一模型加載器的調用。
Model = readModelFromJson(“my.model.json”); 被替換為 Model = (Model)ResourceComponentManager.instance() .loadComponentModel(“my.model.json”);
ResourceComponentManager內部會緩存模型文件的解析結果,並且會自動跟蹤解析過程中發現的所有模型依賴關係,當被依賴的模型發生修改時,會導致所有依賴於它的解析緩存結果自動失效。
可逆計算理論所提出的Y= F(X)+Delta的計算模式可以被封裝到一個抽象的加載器(Loader)接口之中,這一事實極大的降低了在第三方系統中引入可逆計算的成本。詳細介紹參見文章 從張量積看低代碼平台的設計
在Nop平台中,我們對於百度AMIS框架的集成就採用了這種方式。
type: page x:gen-extends: | <web:GenPage view=“MyEntity.view.xml” page=“crud” /> body: - type: form “x:extends”: “add.form.yaml” api: url: “/test/my-action”
通過使用ResourceComponentManager來加載AMIS的頁面文件,我們為它引入了x:extends,x:gen-extends這樣的差量化分解組合機制,可以使用XPL模板語言動態生成JSON頁面內容,可以通過x:extends複用已經定義好的子頁面,並在子頁面的基礎上進行精細化的定製,可以在Delta目錄下增加同名的文件來覆蓋系統中原有的模型文件。
所有JSON、YAML或者XML格式的模型文件都可以直接使用Nop平台的統一模型加載器來實現差量分解、合併。
通過統一模型加載器,我們還可以很容易的將原系統中的模型文件改造為輸出模板文件。例如,我們在Word文件的基礎上約定了一些特殊的表達式定義規則,就可以直接將Word文件轉換為XPL模板語言文件,用於動態生成Word文檔。具體介紹參見如何用800行代碼實現類似poi-tl的可視化Word模板。
四. Delta差量相比於Scala Traits有什麼本質性創新
我在上一篇文章中明確指出Scala語言中的Traits概念可以看作是類空間中的某種Delta差量的定義方式。有些同學讀了這篇文章之後可能會有些疑惑,那麼可逆計算理論中的Delta差量是否本質上也只是某種子類型的定義問題,它並沒有什麼特別的創新之處?
因為很多程序員從學習編程開始就只接觸過面向對象的話語體系,所以在思維中可能會將代碼編寫等價於創建類、屬性、方法。包括在研究ChatGPT如何生成業務代碼的時候,很多人的第一想法也是如何讓GPT****學會將問題分解為多個類,然後再生成每個類對應的代碼。
我們需要明確的是Traits****概念依附於類的概念,但是類並不是對所有邏輯結構的最適合的描述方式。在本文的第一節中,我已經明確指出同一個結構可以放到不同的模型空間中去表達,而在每個模型空間中都存在着對應的、專屬於這個模型空間的差量定義方式。比如一個函數總可以在二進制比特空間、源碼文本行空間這兩個通用的模型空間中得到表達。而類空間本質上也是一個通用的模型空間: 所有使用面向對象技術實現的邏輯結構,都具有類空間中的表達形式,因此也都可以通過類空間的差量來對它們進行Delta修正。
可逆計算理論並不受限於使用某個特定的模型空間,它作為一個理論首先是對眾多分散的實踐提供了統一的理論解釋,並且指出了完整的技術路線應該是Y=F(X)+Delta,將產生式編程(Generative Programming)、面向差量編程和多階段編程有機的結合在一起。在可逆計算的視角下,虛擬化領域的Docker技術、前端領域的React技術、雲計算領域的Kustomize技術等近幾年出現的創新實踐都可以被看作是可逆計算理論的具體應用實例,在這種情況下,我們才可能識別出這些技術之間的共性,並抽象出一種統一的技術架構來將它推廣到更多的應用領域。
可逆計算理論指出我們可以建立更加靈活的領域模型空間,在更加穩定的領域座標系中表達邏輯結構的差量(這一點類似於在物理學中選擇使用內稟座標系(****intrinsic coordinates))。引入領域座標系的概念之後,我們會發現類型系統所提供的是一種並不完善的座標系,有些差量化問題在類型系統中無法得到精確的定義。因為類型概念的出發點就是多個實例可以具有同樣的類型,所以使用它來作為定位座標本身就很可能引入含混性。
可逆計算理論指出類的概念在結構層面可以看作是Map結構:類具有屬性在結構層面對應於根據key可以從Map中獲取到相應的值。類的繼承可以被看作是Map之間的一種覆蓋關係。可逆計算相當於是把這種覆蓋關係推廣到Tree結構之間,並且補充了逆元的概念。Tree是比Map複雜度更高的結構,Tree = Map + Nested。
可以應用於Tree結構的運算必然可以應用到Map結構上,所以Tree可以被看作是對Map的一種推廣。
補充了逆元的概念,相當於是擴大了問題的解空間,一些原先不好解決的問題,在這個新的解空間中都存在通用的解決方案。比如説,Scala Traits不支持取消操作,一旦對象A混入了某個Trait B之後,就無法通過Scala語法實現取消,只能是手工修改源碼,這直接導致很難實現系統級的粗粒度軟件複用。在不修改X的情況下通過補充Delta來實現定製與將X拆解為多個組件重新再組裝的方式有着本質性的區別: 拆解和組裝是具有成本的,而且人工操作可能會引入偶然性的錯誤。這就好像是一支精密的手錶,將它的各個組件拆解後再裝配到一起很有可能會發現某個螺絲擰錯了。
建立領域座標系之後,Delta差量可以跨越傳統的代碼結構障礙,直接作用於指定的領域座標處,這相當於是建立了無所不在的傳送門,我們可以將邏輯差量直接傳送到指定位置處。
在魔法的世界中,走出房間不一定要經過房門,我們可以直接穿牆而過!
為什麼強調樹結構而不是圖結構
Tree結構具有很多優點。首先,它實現了相對座標與絕對座標的統一:從根節點開始到達任意節點只存在唯一的一條路徑,它可以作為節點的絕對座標,而另一方面,在某一個子樹範圍內,每一個節點都具有一個子樹內的唯一路徑,可以作為節點在子樹內的相對座標。根據節點的相對座標和子樹根節點的絕對座標,我們可以很容易的計算得到節點的絕對座標(直接拼接在一起就可以了)。
Tree結構的另一個優點是便於管控,每一個父節點都可以作為一個管控節點,可以將一些共享屬性和操作自動向下傳播到每個子節點。
另一方面,對於圖結構,如果我們選定了一個主要的觀察方向,選擇某個固定的節點作為根節點,那麼我們就可以很自然的將一個圖結構轉換為樹結構。比如Linux操作系統中,一切都是文件,很多邏輯關係都被納入到文件樹的表達結構中,但藉助於文件系統中的文件鏈接機制,本質上可以表達圖結構。所謂的樹僅僅是因為我們在圖上選擇了一個觀察方向而產生的。
五. 系統差量化之後,版本機制還有意義嗎
git的版本相當於是一個比較粗粒度的非結構化差量,可以給一次大的更新起一個名字,可以處理一般的程序源碼。而Delta我們希望它是高度結構化、語義化的,如果所有的語言包括Java都實現合適的Delta差量化,則可以起到類似git的作用。
但另一方面,很多時候我們就想直接修改Delta的實現本身,不需要保留語義邊界,此時用git這種非結構化的方式去管理Delta差量代碼就很合適。
六. XML格式太複雜, 能不能考慮JSON?甚至YAML?
很多程序員並沒有親自設計過XML格式的DSL語言,只是聽業界的前輩講過上古時代的XML是如何被後起之秀淘汰的傳説,就由此形成了一種刻板印象,認為XML過於冗長,只能用於機器之間傳遞信息,並不適合於人機交互。但是,這是一種錯誤的偏見,源於XML原教旨主義對於XML錯誤的使用方式,以及一系列XML國際規範對錯誤使用方式的推波助瀾。
在此前的文章中我已經進行了詳細的解釋,參見GPT用於複雜代碼生產所需要滿足的必要條件.
在Nop平台中我們提供了XML和JSON、YAML之間的自動雙向轉換機制,同樣的DSL同時存在着XML表示和JSON表示。
七. 不完全等價的格式之間如何實現可逆轉換?
有些程序員實踐過DSL描述之間的轉換機制,比如從高層的DSL自動轉換到低層的DSL,此時我們經常會發現要實現可逆轉換是非常困難的,甚至是不可能的。因為跨越複雜性層次或者系統邊界的時候,經常會丟失細節信息,導致轉換前和轉換後僅僅是約等於關係,並不嚴格等價。
有些人寄希望於AI強大的猜測能力,可以根據殘留的信息自動補全得到原始的信息,但這樣做天生就是不精確的,容易出現錯誤的。
A ~ F(B), G(A) ~ B
為了使得上面的兩個方程從約等於轉變為等於,可逆計算理論建議的解決方案是在兩側都補充Delta差量。
A + dA = F(B + dB), G(A + dA) = B + dB
也就是説為了滿足可逆轉換的要求,每一個抽象層都應該提供一個內置的擴展信息保存機制,容納一些當前使用不到的擴展信息。
正所謂有一種用處叫做無用之用,一些可有可無的功能會撐起一個灰色的設計空間,允許意料之外的一些演化在其中發生。
八. 從範疇論的角度如何理解可逆計算
範疇論在抽象數學領域中也能算得上是最抽象的數學分支之一,而一般的程序員其實並沒有接受過很強的抽象數學訓練,所以他們對於範疇論的理解往往侷限在類型系統中,甚至可能和某些函數式語言的語法特性綁定在一起。但是範疇論的本質其實很簡單,也不涉及到類型系統。可逆計算以及Nop平台中的很多做法都可以放到範疇論的理論框架中去理解。
所謂的範疇指的是:
1. 一些點和點與點之間的連接箭頭
2. 箭頭和箭頭可以複合產生新的箭頭,而且箭頭的複合關係滿足結合律
3. 每個點上存在一個單位箭頭
也就是説只要我們能夠把一些概念映射為點和箭頭,那麼就可以很自然的組成一個範疇。
比如説,製作檸檬派的過程可以構成一個範疇。
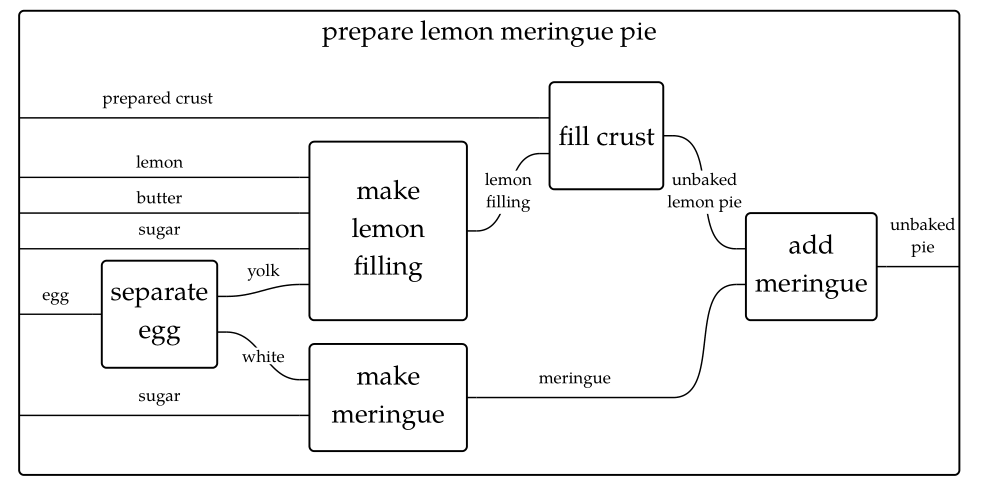
再比如,數據庫的schema定義也構成一個範疇
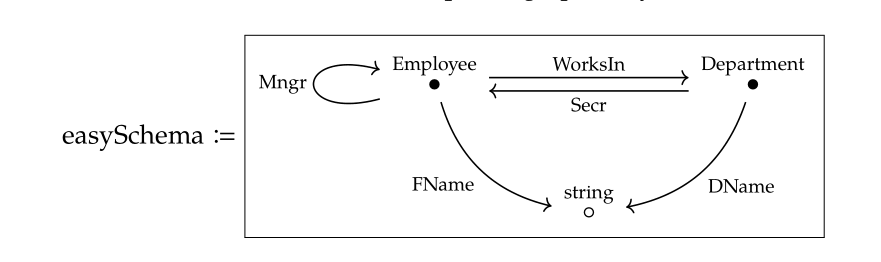
這裏需要注意的是,不是所有的有向圖(Graph)都是範疇,因為範疇要求每個點上都存在單位箭頭,而且箭頭之間需要能夠複合,複合關係還要滿足結合律。數學上更加嚴謹的説法是,從任意一個有向圖出發,我們可以通過Free Construction構造出一個範疇來。所以從下面這種只有兩個箭頭的圖構造得到的範疇實際上包含6個箭頭。
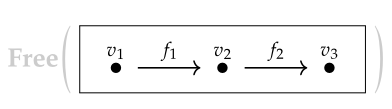
v1,v2,v3上需要增加3個單位箭頭,而f1和f2的複合需要被定義為一個新的箭頭,所以總共有6個箭頭。
這裏的所謂Free指的是我們沒有添加任何新的約束條件,僅僅是從補足範疇論定義的需要出發向圖中補充了最少量的元素。而一個不Free的構造方式是向圖中引入約束條件:規定兩條連接同樣起點和鐘點的路徑是等價的。
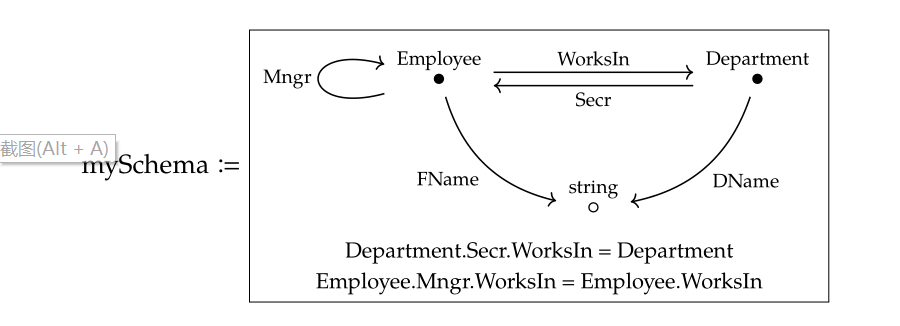
一個比較容易理解的例子是向數據庫的schema關係圖中增加業務約束條件:
• 每個部門的秘書必須在這個部門中工作
• 每個僱員的經理必須和僱員在同一個部門
在easySchema這個範疇上增加equation約束條件之後就可以得到新的範疇 mySchema
以上關於範疇論的示意圖全部出自 Seven Sketches in Compositionality : An Invitation to Applied Category Theory一書。
在範疇論的視角下,我們當前的系統可以被看作是領域結構所構成的範疇,而Delta定製的作用是作用到每一個領域座標處,把領域結構中的每個點映射為一個新的點,由此在整體上把當前的領域結構變換為一個新的領域結構。因此,Delta****定製可以被看作是領域結構範疇之間的映射函子(Functor)。
所謂的函子,就是將範疇C中的每個點映射到另一個範疇D中的一個點,將範疇C中的每個箭頭也映射到範疇D中的一個箭頭,同時保持之間箭頭的複合關係滿足結合律。
注意函子的特殊性在於它作用在範疇C的每個點上,而且映射過程保持範疇C中的某種結構關係。
在Nop平台中,我們很注重以通用的方式來解決問題,這種所謂的通用性可以從範疇論的角度來解釋。比如Excel模型文件解析,一般的做法是針對某個特殊約定好的Excel文件格式,特殊編寫一個Excel文件解析函數,將它解析為某個特定結構的Java對象。而在Nop平台中,我們實現了一個通用的Excel解析器,它並不假定Excel具有特定格式,而是允許相對任意的Excel輸入(字段順序可以隨意調整,允許任意複雜的字段嵌套關係),無需編程就可以將一個Excel文件解析得到對應的領域結構對象。從範疇論的角度觀察,Nop平台所提供的是從Excel範疇到領域對象範疇的一個映射函子,而不僅僅是一個針對特定結構的解析函數。在另一個方向上,對於任意的領域對象,無需編程,就可以使用通用的報表導出機制將它導出為一個Excel文件。這個報表函子與Excel解析函子可以看作是構成了一對伴隨函子(Adjoint Functor)。
九. 這些抽象的理論有什麼用?搞GPT代碼生成能用得上嗎
首先,可逆計算理論本身非常有用,它解決了系統級粗粒度軟件複用的問題。比如説,如果一開始系統底層就遵循可逆計算原理,那麼我們就沒有必要再發明Kustomize技術,Spring容器的實現方式也可以得到大幅簡化。一個銀行核心應用產品如果遵循可逆計算原理,那麼它在不同客户處進行定製化開發的時候,就不需要修改基礎產品的源代碼,大幅降低同時維護多個不同版本的基礎產品代碼的壓力。而革命性的Docker技術在抽象結構層面可以被看作是可逆計算理論的一個標準應用實例,類似Docker的結構構造方式理應可以被推廣到更多的技術應用領域。
第二,從可逆計算理論出發我們可以對GPT代碼生成提出以下幾點建議。
1. 代碼生成並不意味着一定要把代碼拆分為類和方法來生成,類空間不過是通用的模型空間的一種,我們可以採用其他的領域模型空間來表達邏輯。
2. 如果GPT能夠準確的生成代碼,那麼它一定能夠理解元模型和差量模型。元模型可以幫助AI在儘量少的信息輸入情況下精確掌握模型約束條件。而差量模型使得增量式開發成為可能。
3. 在訓練的時候我們可以有意識的使用元模型和差量模型來訓練,這樣可以從少量的樣本迅速衍生得到大量具有內在一致性的訓練樣本。差量化訓練類似於數值空間的梯度下降學習。
基於可逆計算理論設計的低代碼平台NopPlatform已開源:
• gitee: canonical-entropy/nop-entropy
• github: entropy-cloud/nop-entropy
• 開發示例:docs/tutorial/tutorial.md
• 可逆計算原理和Nop平台介紹及答疑_嗶哩嗶哩_bilibili