吳寶珠:伽羅瓦的不朽遺產_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!56分钟前
伽羅瓦的思想仍將持續影響未來幾代數學家。
撰文 | Benjamin Skuse
翻譯 | zzllrr小樂
對於2010年菲爾茲獎得主吳寶珠(Ngô Bảo Châu,1972-)來説,伽羅瓦羣構成了他2009年對數學的開創性貢獻的基礎,他證明了朗蘭茲綱領的“基本引理”,該綱領是2018年阿貝爾獎獲得者羅伯特·朗蘭茲(Robert Langlands,1936-)提出的一系列數學猜想,將許多數學領域聯繫起來。但在第11屆海德堡桂冠論壇(Heidelberg Laureate Forum)的半小時演講中,吳寶珠明智地選擇不去費時間介紹伽羅瓦理論,也沒有嘗試概述朗蘭茲綱領及其相關的基本引理。這些主題過於廣泛、抽象和複雜,難以在如此短的時間內解釋清楚。

取而代之的是,吳寶珠向與會者介紹了伽羅瓦羣,旨在展示為什麼伽羅瓦理論在其誕生之初對數學發展很重要,以及為什麼它在今天仍然是數學進步的核心:這是一種思維方式,允許數學家研究數學的基本結構和形式。
敏鋭的智慧和獨創性
天才數學家、堅定的法蘭西共和主義者和不幸的決鬥者埃瓦里斯特·伽羅瓦(Évariste Galois,1811 - 1832)在世僅短短20年,但他在數學許多分支中留下的遺產已經延續近200年,並且很可能還會持續很長時間。

伽羅瓦最重要的工作是創立了後來被稱為羣論的理論。他提出了關於“羣”的三個基本原則,並利用這些原則發現了羣的更多性質。這些性質可用於將羣與其他看似不相關的羣進行比較。
這種方法可以用來比較不同類型的代數方程以及這些方程的解。更具體地説,伽羅瓦羣包含了多項式方程解之間的所有對稱性;換句話説,根的置換(即重新排列)保留了方程解之間的所有關係。
對於非數學領域的人來説,這似乎都是微不足道的——只是以稍微不同的方式呈現已存在和已知的東西,就像是“洗牌”。但事實上,它過去是、現在依然是一個深刻的啓示。
從巴比倫人到文藝復興時期的意大利
吳寶珠以歷史課開始他的演講:“我們在學校學到的二次方程的解法,你可以在公元前2000年的巴比倫石板中找到等價形式。”即二次方程一般形式ax2+bx+c=0的解:
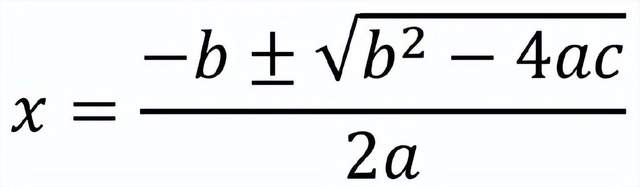
文藝復興時期,意大利數學家喬瓦尼·卡丹 (Gerolamo Cardano,1501-1576;又譯作傑羅拉莫·卡爾達諾)和尼科洛·塔爾塔利亞(Niccolò Tartaglia,1499-1557)寫下了三次方程解的非常複雜的一般形式。“我們當中很少有人能夠自己發現這個公式。”吳寶珠繼續説道,“這是很基礎的,但它有一系列非常巧妙和複雜的變量代換。”這一突破之後,另一位意大利數學家洛多維科·費拉里(Lodovico Ferrari,1522-1565)很快提出了更為複雜的四次方程解法。
在這裏,吳寶珠稍作停頓,他反思並向聽眾問道:“但是我們所説的解是什麼意思呢?我們正在尋找某種(涉及)多項式係數的公式,然後我們可以使用四種運算(加、減、乘、除)得出新的根,但我們會對求根有分歧,因為有多種選擇。”

抽象導致理解

吳寶珠舉了一個例子。“阿貝爾-魯菲尼(Abel-Ruffini)定理表明,不可能找到五次及以上方程的一般形式的解——這是一個驚人的結果,”他説。“但如果給你一個方程,這個定理並不能告訴你是否可以用根式解它。”換句話説,對於一個特定的方程,該定理沒有解釋是否存在僅對方程中的有理係數使用有理數以及加、減、乘、除和求n次根的運算得到方程的解。
“通過伽羅瓦羣,你可以再次證明阿貝爾-魯菲尼定理,並且可以使用伽羅瓦羣的計算來複原塔爾塔利亞和費拉里等人的棘手計算,”吳寶珠説。而且,可解的五次多項式方程正是其對應伽羅瓦羣是可解的。換句話説,伽羅瓦理論可以用來説明一個特定的方程是否可以用根式求解。
當代發展
“伽羅瓦理論的核心意義在於從研究代數方程轉向一個完全不同的對象——某些抽象羣,方程的解可以用這些非常簡單的形式來表達,”吳寶珠解釋道。很久以後,當數學家開始領悟伽羅瓦的洞察時,這種抽象便使伽羅瓦理論成為重要的數學學科,甚至是其他學科之間的基本橋樑。
例如,伽羅瓦理論引入了有限域這一抽象代數概念。事實證明,有限域是從定義算法到公共密碼學、斷層掃描和構建良好計算機網絡等諸多領域的核心。伽羅瓦理論的這些基本、普遍和持久的性質就是它被1994年菲爾茲獎得主埃菲·傑曼諾夫(Efim Zelmanov,1955-)描述為“數學美的黃金標準”的原因(在2024年林道諾貝爾獎得主大會上的海德堡演講期間)。

向不同背景的受眾展示伽羅瓦理論如何滲透到現代純數學絕非易事。吳寶珠從20世紀拓撲學的進展開始講解。“環面是拓撲學中第一個重要的對象,與之相關的是‘基本羣’(fundamental group),”他解釋道,其中基本羣是指與記錄其基本形狀或孔洞信息的拓撲空間相關的羣。
以環面為例,如果你在環面表面縱向畫一個環(下圖藍色),並在環面內部的子午線(經線)上畫另一個環(下圖紅色),則兩者之間無法通過連續變形相互轉換,因此它們是不同的。因此,僅使用這兩種類型的環就可以構建形成環面的空間。這可以表示為環面的基本羣。
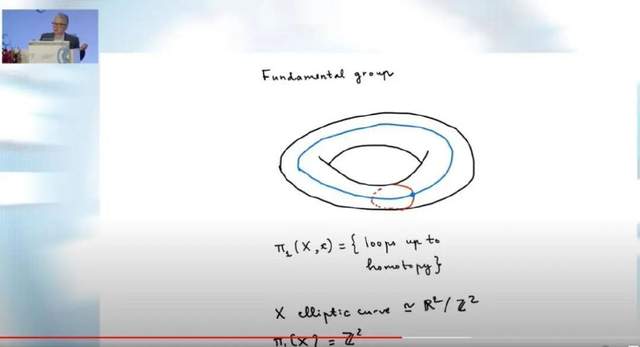
“這似乎與伽羅瓦理論沒有太大關係,但其實有,那就是‘覆蓋理論’(covering theory)。”吳寶珠解釋道。1960年代,亞歷山大·格羅騰迪克(Alexander Grothendieck,1928-2014;1966年菲爾茲獎得主)將所有這些結合在一起,搭建起數論中的伽羅瓦羣與拓撲學中的基本羣之間的橋樑。
我們把細節留給感興趣的讀者,但這裏要説的是,覆蓋本質上是拓撲空間之間的映射,其作用就像底空間(base space)的多個副本到其自身的投影。因此,環面的平凡覆蓋空間可以被描繪成一個以螺旋樓梯形式最終回到圓環的圖景,即底空間。在一定的限制和條件下,給定底空間的基本羣類似於伽羅瓦羣。由此,拓撲空間和域之間的聯繫和相似性就變得顯而易見,這為這兩個學科提供了新的見解。

吳寶珠隨後將話題快進到今天。他説算術幾何中一些最大的問題與伽羅瓦理論有關。例如:“如何表徵上同調(cohomology,通常與拓撲空間相關的阿貝爾羣序列)代數簇中出現的伽羅瓦表示,”他問道。“我們通過這些伽羅瓦表示來研究代數簇,但我們需要知道這些伽羅瓦表示的性質。”
他提到在過去20年裏,儘管包括他本人在內的許多人在這個問題上取得了顯著進展,但它仍然可能要讓數學家研究50到100年的時間。實際上,吳寶珠的結論是,伽羅瓦的思想在他和所有受眾去世後依然具有重要意義。
實現預言
在1832年5月30日那場結束他生命的決鬥的前一天晚上,伽羅瓦瘋狂地寫下了60頁的數學筆記。這些筆記經常被浪漫地認為是羣論誕生的原因,儘管事實證明他前期完成的工作才是起決定性作用的。然而,它們確實包含了一個預言性的後記:“我希望,以後會有一些人充分利用它來破譯這一切混亂。”
如果伽羅瓦能夠聽到吳寶珠解釋他的原創思想,以及數學進步如何繼續影響和塑造21世紀的數學,毫無疑問,他會感到很滿意,因為已經遠遠超出了他的期望。
你可以在下面的視頻中觀看吳寶珠在第11屆海德堡桂冠論壇上的完整演講:
本文經授權轉自“zzllrr小樂”公眾號,原標題《小樂數學科普:菲爾茲獎得主吳寶珠談論伽羅瓦的不朽遺產——譯自HLF海德堡桂冠論壇》。《返樸》對譯文進行了校訂,本文譯自Benjamin Skuse, Galois’ Enduring Legacy,原文鏈接:https://scilogs.spektrum.de/hlf/galois-enduring-legacy/

1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。