希爾伯特第6問題:他們能為牛頓力學找回時間的方向嗎?_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!52分钟前

撰文 | 嘉偉
曾經看到過一種非常有詩意的説法:牛頓力學消除了時間的方向。如若回憶一下經典力學基礎的牛頓三大定律,就可以發現,定律的描述之中是沒有時間方向這一參數的。這也意味着,在一個時間倒流的宇宙裏,經典力學的表述形式將和我們所熟知的並無任何差異。這種理論性質一般被稱為時間反演對稱性。
2006年的IMO(國際數學奧林匹克競賽,International Mathematical Olympiad)金牌得主鄧煜,當年被保送至北大數學系,2年之後又轉去了麻省理工學院(MIT)繼續研讀數學專業。如今他已經是頗有建樹的青年數學家,現為芝加哥大學副教授。他和密歇根大學數學系教授Zaher Hani,以及密歇根大學助理教授馬驍(本科畢業於中科大少年班)組成的團隊(簡稱為DHM團隊)在2025年3月3日於arXiv上貼出文章,宣稱解決了希爾伯特第6問題。


雖然125年前提出的希爾伯特第6問題,主旨是物理學的公理化,但如果追溯其歷史淵源,可以發現希爾伯特在闡述該問題的時候,未嘗沒有將熱力學第二定律所刻畫的宏觀現象歸結於微觀機械行為的動機。所以從一個浪漫且稍顯誇張的角度來説,如果經驗證無誤的話,鄧煜等人的論文在某種意義上相當於為牛頓力學找回了時間的箭頭。
當然,實際上牛頓力學是一個很寬泛的概念,它包含了三體問題、KAM定理,等等。本身就可以説牛頓力學藴含了時間的單向性,這些則遠非當代數學家的功勞。
時間之矢:經典力學與熱力學的緊張關係
早在17世紀,艾薩克·牛頓(Isaac Newton)就開始對運動擴散的不可逆性現象產生了濃厚的興趣,特別是它似乎還關乎機械宇宙是否還需要神學介入的問題。牛頓認為,一般地説,“運動多是失去容易得到難,總是趨於退化。”
等到18世紀和19世紀早期,人們開始注意到,有很多自然現象似乎並無時間反演對稱性。比如説氣體的擴散、摩擦力的耗散、熱量總是從温度高的物體流向温度低的問題……名為熱力學的物理學分支開始發展出一個統一的理論框架,德國數學家和物理學家魯道夫·克勞修斯(Rudolf Clausius)在1865年第一次提出了熱力學第二定律的現代表述:宇宙的熵總是趨於最大。
但這和時間的方向性又有何關係呢?請細想一下我們是怎麼知道時間是有方向的?
如果播放一段視頻,畫面裏有個杯子落到地上,摔成了碎片。沒有人會覺得這一過程有什麼不自然的問題。但是,如果看到地上四散的玻璃碎片躍起,拼成了一個完整的玻璃杯,我們都會意識到,這段視頻是倒放的!
上面簡單的思想實驗其實揭示了我們認知時間的方式,而這一方式本質上是人類對熱力學第二定律的樸素經驗——就算完全不瞭解熱力學第二定律的人,因為世界上的萬事萬物都受其制約,所以通過身邊的現象,自然會對這一基本物理學定律有所感知。
19世紀中葉,新生的熱力學理論享有一段與牛頓力學沒有明顯衝突的短暫安寧時期。詹姆斯·克拉克·麥克斯韋(James Clerk Maxwell)和路德維希·玻爾茲曼(Ludwig Eduard Boltzmann)把氣體分子的運動理論和統計學上的概念聯繫了起來。玻爾茲曼更是首次把統計力學與熱力學第二定律之間的聯繫,闡釋得明明白白。
麥克斯韋引入了著名的分子混沌假設。它假設兩個發生碰撞的粒子的速度是彼此不相關的,並且與具體位置無關。這意味着可以通過分別考慮每個粒子的概率來計算一對具有給定速度的粒子碰撞的概率,而忽略找到一個具有速度v的粒子和找到另一個具有速度v′的粒子的概率之間的相關性。這個假設是玻爾茲曼方程的關鍵成分,它允許從 BBGKY 層次結構(描述多粒子系統中各個粒子的分佈函數)過渡到玻爾茲曼方程,玻爾茲曼用它推導出了氣體分子的熱力學第二定律——H定理(H-theorem)。
他們的方法是把氣體分子看作是剛性的小球,根據小球速度的統計分佈,可以得到氣體宏觀行為的特徵——如根據分子運動來描述的熱現象,畢竟温度就是物體內部分子或原子的平均動能的量度。
但有個更加基本的問題:考察單個分子小球,沒有什麼神秘的力量迫使它遵循熱力學第二定律,它僅僅是遵照一般的動力學定律,運動、碰撞、改變路徑……全部過程都是可逆的,每個分子也都是如此,但是在整體上,最終實現了熱力學第二定律所指向的單一結果。而這種確定的方向性——如温度不同的氣體混合在一起,最終温度會變得均勻——我們通常就認為,這是時間的方向!
或許有讀者會猜測,熱力學定律與經典力學存在“矛盾”,是否是因為它其實是量子現象?遺憾的是,量子力學裏的薛定諤方程也是時間反演對稱的。實際上幾乎所有的物理學定律都滿足時間反演對稱性,像熱力學第二定律這樣有時間方向性的定律反而是少數派。
質疑:從物理過渡到數學
不出所料,這個深奧的物理問題自然而然地引出了深奧的數學問題……以及爭端。
約翰·洛施密特(Johann Josef Loschmidt)是奧地利的科學家,在熱力學、光學、電動力學和化學領域做出了開創性的工作。他雖是玻爾茲曼的好友,但無法接受從時間對稱的動力學和形式中推導出不可逆的過程!在科學史上,從時間對稱的動力學和形式中推導出不可逆的過程被稱為洛施密特悖論。
洛施密特並不孤單,實際上大名鼎鼎的數學家和邏輯學家恩斯特·策梅洛(Ernst Zermelo)也反對統計力學。策梅洛是如今數學界使用最廣泛的公理系統——策梅洛-弗蘭克爾公理系統(ZF,如果加上選擇公理則是ZFC)——的創建者之一。他意識到,玻爾茲曼的H-定理與亨利·龐加萊(Jules Henri Poincaré)的迴歸定理相互衝突。龐加萊是那個時代的數學界領袖,拓撲學上著名的龐加萊猜想正是他提出的。
龐加萊迴歸定理(Poincaré Recurrence Theorem)斷言對於某類孤立的力學系統,只要經過足夠長的時間,系統一定會回到一個與初始狀態任意接近的狀態,或者返回到初始狀態本身。這個定理適用於守恆系統,即系統的總能量和體積保持不變。龐加萊迴歸定理的核心思想是,在一個有限體積的相空間中,系統的軌跡會在時間演化中不斷遍歷這個空間,最終會回到初始狀態或其附近。換句話説,模擬稀薄氣體分子的大量小球,可以演化到無限接近初始時的狀態。這就違背了熱力學第二定律。
玻爾茲曼對此做出的解釋,也是現代教科書普遍採用的解釋是:統計力學是基於統計的,而龐加萊迴歸所需時間的期望值,遠遠超過宇宙的現有壽命,所以系統在幾乎所有時間裏都是滿足熱力學第二定律的,這體現了熱力學定律在宏觀上的統計意義。
統計力學奠基人路德維希·玻爾茲曼於 1905 年訪問了美國加州新成立的斯坦福大學,在日記裏寫道:“在歐洲,如果一個富婆發瘋了,她會給自己買一打貓或一隻鸚鵡;而在這裏,她會聘請一流的建築師,建造一所大學。”

經過幾次質疑和反駁,玻爾茲曼的統計力學開始被人們接受。但最開始的問題仍困擾着那個時代的數學家:能否摒棄未經證明的假説,單純藉助經典力學推導出玻爾茲曼方程(相當於説從時間可逆的機械力學系統演化出時間不可逆的熱力學系統)?如果不能的話,是不是説明用於構建玻爾茲曼方程的那些假説,本身是一個需要客觀承認的新物理事實(定律)?
回應:希爾伯特第6問題
在1900年的巴黎國際數學家大會,歷史地位至少與龐加萊相當的數學巨人大衞·希爾伯特(David Hilbert)在演講中提出了著名的23個“面向未來”的問題。
其中第6個問題:
“對幾何基礎的研究提出了這樣一個問題:以公理化的方法同樣處理那些當今數學已發揮重要作用的物理科學;其中首要的是概率論和力學。……玻爾茲曼關於力學基本原理的工作提出了這樣一個問題:如何在數學上發展那些僅被初步闡明的極限過程,進而從原子論的觀點推導出連續介質的運動定律。”
這裏大家也能看到,希爾伯特第6問題是非常寬泛的,最終目標是把整個物理學公理化,但是在問題的進一步闡述中,他特意提及了玻爾茲曼方程和(經典)力學的關係。結合前文介紹的背景,也能反推出當時學界對玻爾茲曼的統計力學的不信任程度,以及希爾伯特迫切期望澄清“可逆的動力學過程如何演化出不可逆結果”的數學本質。
後者(而非為物理學進行公理化)也是DHM團隊意圖攻克的難題。
歷史上對該問題後半部分的常規理解是,從稀薄氣體的動力學玻爾茲曼方程到可壓縮氣體動力學的連續歐拉方程和不可壓縮的納維-斯托克斯-傅里葉方程的過渡。但是少有數學家嘗試去從牛頓力學推出玻爾茲曼方程。
直到1975年,美國數學家Oscar Erasmus Lanford證明了Lanford定理。他基於粒子均為球對稱粒子彈性碰撞的假設,證明了在足夠短的時間內玻爾茲曼方程的正確性。近年來歐洲的數學家們(如Laure Saint-Raymond,Isabelle Gallagher等人)對此問題進行了深入的研究,但希爾伯特第6問題需要對任意長的時間證明玻爾茲曼方程的正確性,在這點上並無突破進展。
主要困難來自於證明不同粒子的(漸近)獨立性的假設是合理的,也就是前文提及的分子混沌假設。這被證明更具挑戰性。事實上,最新論文的三位作者甚至花了一些時間才把它作為一個具體的數學問題來正確地闡釋。
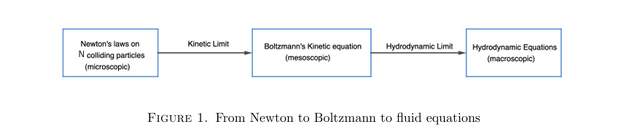
DHM團隊嘗試解決這一歷史遺留問題,進而完全打通“從牛頓到玻爾茲曼到流體方程”的過程。
他們以及歷史上對“狹義”希爾伯特第6問題的解答,比起為物理學(某個分支)構建一套公理系統(並證明其相容性),更像是證明純粹的數學問題(雖然這個問題的背後有豐富的內涵和歷史,乃至深刻的哲學),大意如下:
根據控制微觀粒子相互作用的牛頓定律,對流體的宏觀方程(如歐拉方程和納維-斯托克斯方程)給出數學上嚴格的推導,其中,玻爾茲曼動力學方程的推導是一個關鍵的中間步驟。換句話説,這個問題需要證明兩個極限的合理性:(i)動力學極限,即在適當的極限N → ∞中,從N粒子系統的(微觀)牛頓力學傳遞到單粒子密度函數的玻爾茲曼動力學方程,以及(ii)流體力學極限,即在碰撞頻率趨於無窮大的極限中,從玻爾茲曼動力學方程傳遞到流體運動的(宏觀)方程。
單個水分子就像是一個小球,足夠多的水分子則可以構成水蒸氣。當分子小球彼此始終處於碰撞中,我們可以説它們“黏”在了一起,變成了連續的液體。
把上面樸素的思路進行理論化,就得到了數學物理中的kinetic limit的概念。它通常用於描述從微觀動力學到宏觀行為的過渡。它涉及研究當系統中粒子數量趨於無窮大且粒子間的相互作用範圍趨於零時,系統的行為如何演化。在玻爾茲曼動力學理論中,kinetic limit是推導玻爾茲曼方程的關鍵步驟。通過這種極限過程,可以從粒子系統的微觀動力學(如牛頓定律)推導出描述宏觀行為的動力學方程(如流體力學方程)。這一過程通常被稱為 Boltzmann-Grad 極限,它是稀薄氣體分子運動理論的基礎。
DHM團隊的論文有48頁,但是要想吃透裏面的內容,則需要對這一領域有全面且深入地理解。至少還需要閲讀歷史上數十篇相關的論文,像他們之前在2024年11月發表的164頁論文,就是為最後一篇所做的準備工作。
另外值得一提的是,數學界有所謂的四大頂刊:Annals of Mathematics(《數學年刊》)、Inventiones Mathematicae(《數學新進展》)、Acta Mathematica(《數學學報》)和Journal of the American Mathematical Society (JAMS)(《美國數學會雜誌》)。在這些期刊上發表論文的難度極高,能夠在其中發表文章是數學家學術生涯中的重要成就。剛剛進入研究領域並不算久的鄧煜,已在其中三家刊物上發表過論文。最近兩年更是連續有論文被頂刊所採用。

他們最新的論文,就算是偏微分方程領域裏的專家學者,也需要漫長的時間來研讀審閲,才能做出評價。筆者限於自身的水平,更無可能對文章進行深入的分析和講解,乃至做出評判。但還是可以糾正一些媒體的報道。比如,有一篇報道提到,他們主要通過4個步驟實現突破,其中第四步是“熵產生機制,通過碰撞序列的馬爾可夫性解釋時間箭頭起源”云云,這部分疑似由AI生成……按照他們團隊的思路,完全不需要解釋熵產生機制——他們只需要從牛頓力學推出玻爾茲曼方程,後者原本就藴含H-定理。從前文可知,H-定理相當於針對氣體的熱力學第二定律。此外在論文中也沒有看到關於馬爾可夫性的應用。
雖然他們的成果還需要等待漫長的同行評議過程,但學術界普遍比較樂觀。現在北大國際數學中心正在組織研討會,已經邀請鄧煜和馬驍於3月17日至22日作5天報告。
鄧煜現就職於芝加哥大學的數學系,在他的個人主頁上有如下個人介紹:
喜愛詩歌、故事、小説、拼圖、漫畫、圍棋、足球以及任何美麗迷人的事物。
誠哉斯言。
參考資料
[1]Yu Deng, Zaher Hani, Xiao Ma, Hilbert’s sixth problem: derivation of fluid equations via Boltzmann’s kinetic theory, arXiv:2503.01800
[2]Yu Deng, Zaher Hani, Xiao Ma, Long time derivation of the Boltzmann equation from hard sphere dynamics, arXiv:2408.07818
[3]鄧煜芝加哥大學的個人主頁https://mathematics.uchicago.edu/people/profile/yu-deng/
[4]Yu Deng,https://www.zhihu.com/question/34782710/answer/354811354

1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權説明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。