為什麼在圓周率中會出現26390和你的生日? | 袁嵐峯_風聞
风云之声-风云之声官方账号-31分钟前
如果你知道圓周率約等於3.14,那麼你的數學至少達到了小學水平。這就是為什麼,聯合國科教文組織2019年把每年的3月14日設置為“國際數學日”。
如果你知道圓周率是個無理數,即它是無限不循環小數,那麼你的數學至少達到了中學水平。由此決定,再強的計算機也不可能把π算盡。有時看到一羣民科大談如何把π算盡,大談這如何意味着揭開宇宙秘密,實在令人啼笑皆非。

如果你知道圓周率是個超越數,即它不是任何整係數多項式的根,那麼你的知識水平超過了99.9%的人。由此決定,化圓為方不可能用尺規作圖完成。任何還在研究這個問題或者三等分角、立方倍積等經典的不可能問題的人,都純粹是在浪費時間。
如果你還知道圓周率下面的性質,那麼你的知識水平至少超過了99.99%的人。
最近,中國科學技術大學上海研究院墨子沙龍邀請中國科學院數學與系統科學研究院袁亞湘院士做了一場報告《數學漫談》(袁亞湘院士:刷題能學好數學嗎? | 墨子沙龍)。袁亞湘院士是中國數學會前理事長,他這場報告一開頭就講了不少π的有趣性質。

有很多意想不到的公式得到π。例如:
1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + …
你猜,這樣無窮下去等於多少?答案是π/4。
作為一種數值方法,這樣可以計算π,但缺點是收斂得太慢。你可以用下面這種快得多的方法:
1 + 1/2^2 + 1/3^2 + 1/4^2 + …
你猜,這個無窮級數又等於多少?答案是π^2/6。
這兩個公式都還比較簡單,至少我在上大學的時候都學過。如果你能證出它們,那麼你的數學至少是大學水平。但下面這個公式,就有點天外飛仙了:
π = Sigma(k = 0, infinity) (1/16^k) * [4/(8k+1) - 2/(8k + 4) - 1/(8k +5) - 1/(8k +6)]
我不知道這個公式是怎麼來的,但至少它的形式還比較簡單。如果我努力鑽研一番,也許是能搞明白的。而且很容易就能看出,這個公式收斂得很快,因為每一項前面都有個除以16的k次方,隨着k的增加它會迅速減小。
令人震驚的是,還有下面這種完全神來之筆的公式:
1/π = sqrt(8) / 9801 Sigma(n = 0, infinity) [(4n)!/(n!)^4] * [(26390n + 1103) / 396^(4n)]
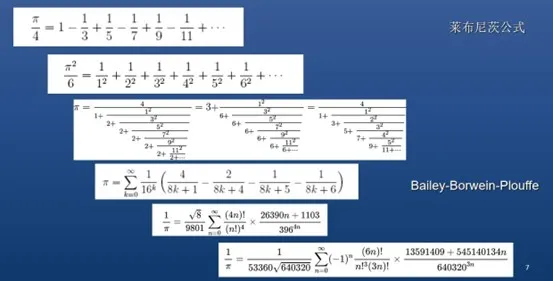
這個公式來自印度傳奇數學家斯里尼瓦瑟·拉馬努金(Srinivasa Ramanujan,1887 — 1920)。他的特點是經常提出令人目瞪口呆的恆等式,這就是他的代表作之一。為什麼計算圓周率會出現26390這麼大的數,我完全看不出原因!希望有專家能給我和公眾指點一番。

這個公式收斂得更快,每計算一項可以得到8位的十進制數字。1985年,有人用它把π計算到了1750萬位。
可是這還沒完。袁亞湘舉的最後一個公式是:
1/π =1/ [53360 sqrt(640320)] Sigma(n = 0, infinity) (-1)^n * {(6n)!/[(n!)^3 (3n)!] } * [(545140134n + 13591409) / 640320^(3n)]
有了前面的鋪墊,我雖然還是會對這公式的複雜程度感到震驚,但很快就可以明白,它跟拉馬努金公式是基於相同的原理,因為它們的結構如出一轍。只要能理解拉馬努金公式,肯定也能理解這個更復雜的,只是下多少功夫的問題。仔細看,雖然這裏最大的數是545140134這個九位數,但最特別的是640320,它出現了兩次,分別在連加前面的根號下和連加中的3n次方那一項。由此可見,這裏肯定有某種訣竅。
事實上,搜索一下就可以知道,這是大衞·丘德諾夫斯基和格雷高裏·丘德諾夫斯基兄弟在1989年提出的,正是對拉馬努金公式的改進。用這個公式,計算一項就可以得到15位的十進制數字。1994年,丘德諾夫斯基兄弟用這個公式把π計算到了40億4400萬位。袁亞湘告訴大家,最近π算到了105萬億位。

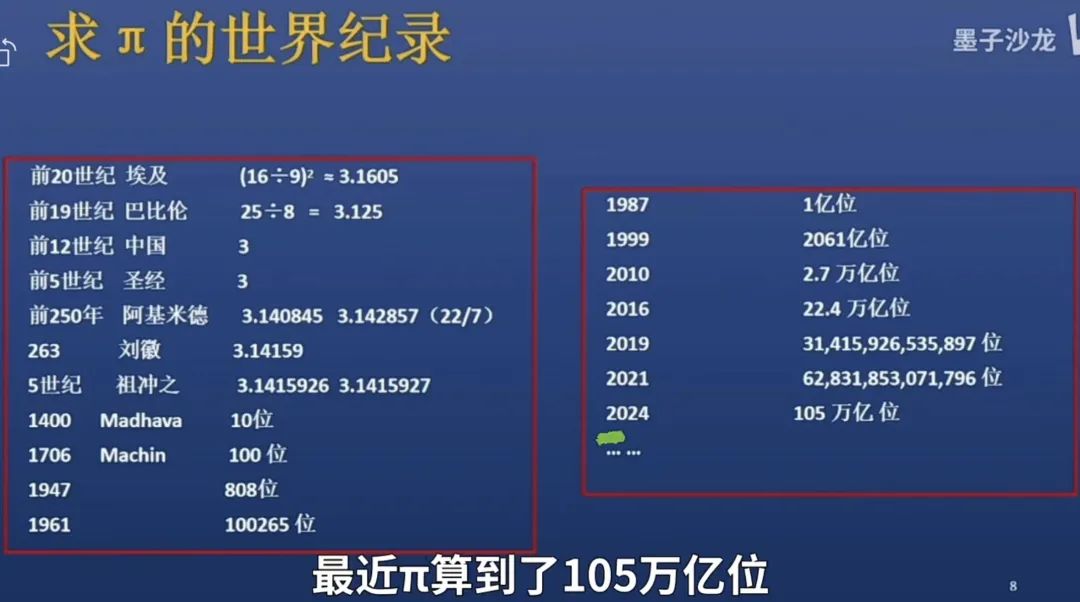
緊接着,袁亞湘又説了圓周率的一個性質。你如果明白他説的是啥,你的知識水平就超過了99.999%的人。他的原文是:
π有一個有待證明的有趣性質:把身份證號碼輸進去,在π裏能找到,比如19210701是黨的生日,精確在4400多萬位就能找到這個數串。同樣道理,輸入共和國的生日19491001也能找到,但稍微難一點,在8200多萬位。所以我經常開玩笑:π告訴我們,先有共產黨後有新中國。當然一般來説,數串越長越難找。如果輸入1314,很快就能在小數點後3902位找到,但如果在1314前面加520,就難多了,在200多萬位才能找到。彷彿告訴我們:一生一世很容易,但要愛一個人一生一世還是挺難的。
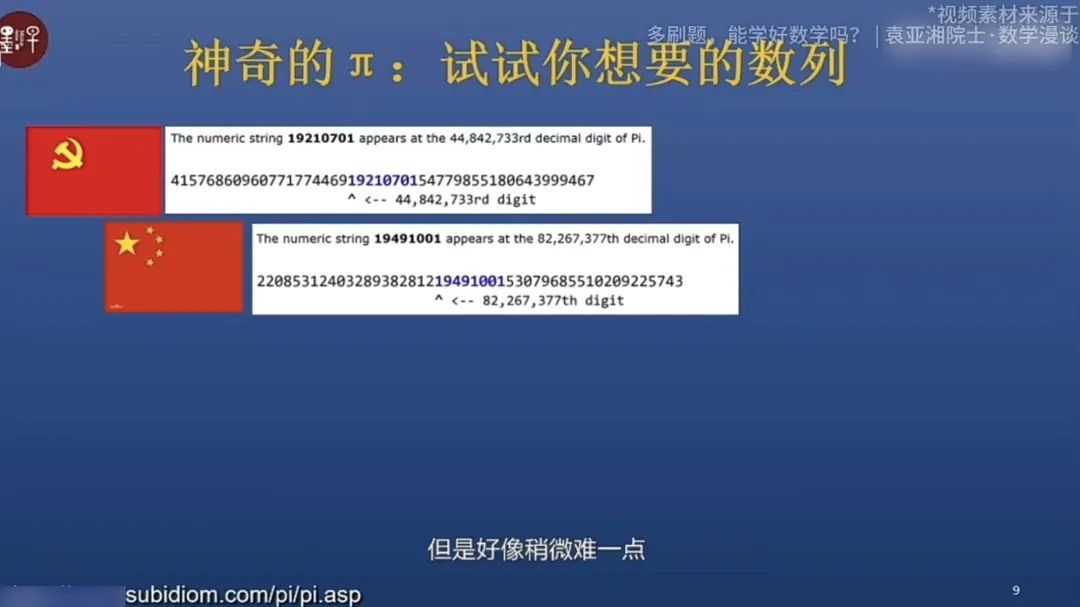
你看明白了嗎?其實袁亞湘説的是這樣一個性質:在圓周率的小數表示中,包含所有可能的自然數序列。請注意,這個性質還沒有證明,也就是説π是不是真的包含所有的自然數序列,我們是不知道的。現在能説的,只是我們嘗試了很多序列都找到了,而且到目前為止沒找到反例。
再搜索一下,可以發現滿足這樣性質的數字叫做正規數(normal number)。實際上,正規數的定義比這個更嚴格一些,它還要求所有等長序列出現的概率相等,都等於它們在完全隨機序列中出現的概率。不過對我們這些數學門外漢來説,暫時不用在意這些細節。
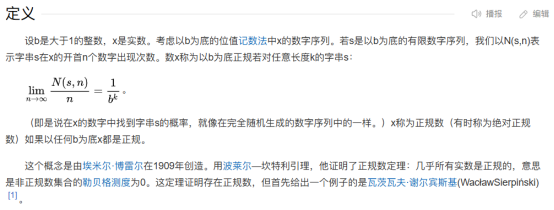
正規數的意義可以這樣理解:假如把自然數序列作為一種編碼,那麼在正規數中可以找到任何信息,包括你的生日、你的電話號碼、你的所有信息,包括古往今來所有的書籍、所有的圖片、所有的影視,包括外星人的所有信息,包括以後可能產生的任何信息。這真是令人神往,唯一的問題只是我們沒有那麼多時間去瀏覽那麼多信息。
有朋友問,是不是所有的無理數都有這樣的性質?回答是,顯然不是。因為我們可以構造一個只由0和1組成的無理數:
0.101001000100001...
這個數的特點是,兩個1之間的間隔越來越長,分別是一個0、兩個0、三個0、四個0等等。顯然它不是循環小數,因此它是無理數。但有很多序列,在它當中就找不到,例如包含0和1之外數字的,以及包含相連的兩個1的。因此,它不是個正規數。
朋友又問了:那根號2呢?它是不是正規數?
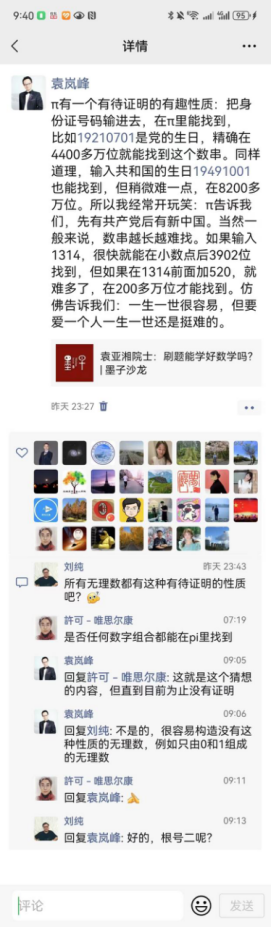
答案又一次讓人震驚。人類目前對正規數的瞭解處於一個很神奇的狀況:一方面我們知道它特別多,簡直遍地都是,但另一方面我們又很難舉出一個具體的例子。
先來看前一面。正規數特別多的意思是,我們可以證明幾乎所有的實數都是正規數。“幾乎所有”的意思是,非正規數的測度是0,也就是説它們在實數中所佔的比例是0。
當然,測度為0不意味着不存在。顯然非正規數是大量存在的,所有的有理數都是非正規數,因為它們的小數表示會循環。但你如果學過實數的性質,你就會知道有理數在實數中所佔的比例是0。當然,如果能瞭解這些,你的知識水平本來就超過99.99%的人了!現在我們知道的是,所有的有理數加上所有的非正規的無理數,在實數中所佔的比例還是0。
再來看後一面。雖然隨便拎出一個實數來,它就有極大的概率是正規數,——實際上這個概率是100%,因為它不是正規數的概率是0%,——但100%的概率並不等於必然發生。最神奇的是,對於任何一個你容易想到的無理數,例如π或者根號2或者ln2或者e等等,我們目前都不知道它是不是正規數!
事實上,正規數這個概念是法國數學家埃米爾·博雷爾(Félix-Édouard-Justin-Émile Borel,1871 — 1956)在1909年提出來的。他立刻就證明了幾乎所有的實數都是正規數,但第一個已知的正規數,卻要等到1917年才由波蘭數學家瓦茨瓦夫·謝爾賓斯基(Wacław Franciszek Sierpiński,1882 — 1969)構造出來。對於那些不是專門構造出來的數,也就是常見的π或者根號2等等數,要判斷它是否正規非常困難。


類似的窘境在數學裏經常出現。例如我們知道π和e都是無理數,但它們倆加起來是不是無理數?居然還沒人知道!雖然從直覺來看,π + e幾乎不可能是有理數,但目前沒人能證明這一點。
現在,你對數學的博大精深,是不是有了更多的感悟呢?