為什麼需要復變信息論_風聞

為什麼需要復變信息論

    2024年12月16日著名的《自然》雜誌網站上發表了一篇叫《Why probability probably doesn’t exist (but it is useful to act like it does) 的文章，探討一直讓普通人迷惑的概率本質。文章的標題十分抓人眼球，文章也追溯了對概率概念不同觀點的歷史資料。但是文章最後並沒有給出明確的判斷。文章作者在最後的結論是“在我們的日常生活中，概率可能並不存在——但假裝它存在往往很有用。”

    本文將從全新的視角來嘗試解釋概率和信息論，以及為什麼我要將複數引入概率和信息論，以及複數概率以及復變信息論的基本特點和應用場景。

一．概率論和信息論

1.1）古典概率定義

古典概型也叫傳統概率、其定義是由法國數學家拉普拉斯 (Laplace ) 提出的。如果一個隨機試驗所包含的單位事件是有限的，且每個單位事件發生的可能性均相等，則這個隨機試驗叫做拉普拉斯試驗，這種條件下的概率模型就叫古典概型。

（1） 試驗中所有可能出現的基本事件只有有限個；

（2） 試驗中每個基本事件出現的可能性相等。

具有以上兩個特點的概率模型是大量存在的，這種概率模型稱為古典概率模型，簡稱古典概型，也叫等可能概型。

1.2）現代概率定義

柯爾莫哥洛夫於1933年給出了概率的公理化定義，如下：

設E是隨機試驗，S是它的樣本空間。對於E的每一事件A賦於一個實數，記為P(A)，稱為事件A的概率。這裏P(A)是一個集合函數，P(A)要滿足下列條件：

（1）非負性：對於每一個事件A，有P(A)≥0;

（2）規範性：對於必然事件，有P(Ω)=1;

（3）可列可加性：設A1，A2……是兩兩互不相容的事件，即對於i≠j，Ai∩Aj=φ，（i，j=1，2……），則有P(A1∪A2∪……)=P(A1)+P(A2)+……

1.3）經典信息論定義

第一階段：經典信息論（1940s-1960s）

以克勞德·香農1948年發表的《通信的數學理論》為標誌，首次建立信息傳輸的數學模型。提出信息熵量化信息不確定性，信道容量定理揭示通信速率極限，信源信道分離定理確立編碼分層理論。這一階段聚焦點對點通信系統，解決’如何可靠傳輸’的核心問題，奠定信息論學科基礎。

第二階段：近代信息論（1970s-1990s）

研究範圍從單節點擴展至網絡環境，突破香農單用户模型侷限。網絡信息論研究多用户信道容量域，信源編碼發展出矢量量化、分佈式編碼等技術。糾錯碼領域取得重大進展，如卷積碼的維特比譯碼算法、Turbo碼逼近香農極限。該階段理論成果支撐了移動通信（如GSM）和互聯網協議的發展。

1.4）現代信息論定義

第三階段：現代信息論（2000s-至今）

量子信息論突破經典物理限制，量子糾纏通信、量子密鑰分發成為研究熱點。生物信息學應用信息熵分析基因序列，壓縮感知理論重構稀疏信號。新型編碼技術如LDPC碼支撐5G通信，人工智能與信息論深度融合推動深度學習中的信息瓶頸理論發展。研究範疇已拓展至物理、生物、計算等多個學科交叉領域。

二．量子概率論和量子信息論

2.1）量子概率定義

概率幅（Probability amplitude）和概率（Probability）

概率幅（Probability amplitude）和概率（Probability）是量子力學中密切相關的兩個概念，但它們有着不同的物理意義和數學定義。

性質：

概率幅是一個複數，通常寫成 ψ(x)=a+bi（其中 a 和 b 是實數，i 是虛數單位）。

概率幅的大小與一個事件發生的可能性相關，但本身並不能直接表示概率。

在數學上，概率幅的平方的模值（絕對值的平方）給出概率。

數學表達： 如果粒子處於狀態 ∣ψ⟩，那麼該粒子在位置 x 處被發現的概率幅是： ψ(x)=⟨x∣ψ⟩

其中，⟨x∣ψ⟩ 是量子態 ∣ψ⟩ 在位置態 ∣x⟩ 下的投影。

2. 概率（Probability）

概率是一個實數，表示某個事件發生的可能性，數值範圍為 0 到 1。在量子力學中，粒子在某個位置被發現的概率與概率幅的絕對值平方相關聯。

數學定義： 如果某個量子態的概率幅為 ψ(x)，那麼粒子在位置 x 被找到的概率 P(x) 是： P(x)=∣ψ(x)∣^2 其中，∣ψ(x)∣^2 是概率幅的複數模平方，即： ∣ψ(x)∣^2=ψ(x)ψ∗(x)

這裏 ψ∗(x) 是概率幅的共軛複數。

概率幅與概率的關係

概率幅是一個複數，包含了事件發生的幅度和相位信息。

概率是概率幅的模平方，即 ∣ψ(x)∣^2，是一個實數，表示某事件發生的可能性。

1. 概率幅（Probability Amplitude）

在量子力學中，系統的狀態由一個波函數（wave function）或態矢量來描述，通常表示為 ψ（或 ∣ψ⟩ ）。這個波函數的每個位置 x 或動量 p 對應的複數值稱為概率幅，記為ψ(x)或⟨x∣ψ⟩。

2.2）量子信息定義

馮·諾依曼熵在量子信息理論中扮演重要角色。當系統信息完備，其狀態由態矢量描述，稱為純態，用密度矩陣算符亦可表示。在量子信息論中，香農熵被推廣為馮諾依曼熵(Von Neumann Entropy)：S(ρ)≡−Tr(ρlog2⁡ρ)=H({λi})

其中 {λi} 是密度矩陣 ρ 的本徵值。

三．可觀察性與概率論

對於概率 的解釋，大體分為 頻率説和主觀説。

該學派認為，概率是客觀現象的內在屬性，可通過大量重複實驗來估計其數值。

主觀説任務，概率是信念強度(Degree of belief)，本質上源於人固有的知識和直覺。

四．不可觀察性與量子概率論

量子力學最聞名的特點就是測量的結果即使從原理上也無法完美預測。我們最多隻能算出各種可能情況的概率。其中的數學關係以波恩定則確定：波函數會給每種測量結果分配一個“概率幅”，該結果出現的概率等於其對應幅值的平方。

量子力學的基本原理

非定域性有時也稱為不確定性，是指某個或某組量不確定在其定義範圍內更小的確定範圍內的性質。在量子力學中，某個物理量不確定在其定義範圍內更小的確定範圍的性質，稱為量子非定域性。不確定性原理（Uncertainty principle），又稱“測不準原理”、“不確定關係”，是量子力學的一個基本原理，由德國物理學家海森堡（Werner Heisenberg）於1927年提出。

該原理表明：一個微觀粒子的某些物理量（如位置和動量，或方位角與動量矩，還有時間和能量等），不可能同時具有確定的數值，其中一個量越確定，另一個量的不確定程度就越大。測量一對共軛量的誤差（標準差）的乘積必然大於常數h/2π（h是普朗克常數）是海森堡在1927年首先提出的，它反映了微觀粒子運動的基本規律——以共軛量為自變量的概率幅函數（波函數）構成傅立葉變換對；以及量子力學的基本關係（E=h/2π*ω，p=h/2π*k），是物理學中又一條重要原理。

五．客觀性與主觀性

要定義概率有幾種方法，大致分為兩派。“客觀”或者“物理性”的觀點將概率視為系統的一個基本性質。頻率學派是對概率的一種客觀解讀，將概率視為多次實驗的結果，如上述的投擲硬幣例子。

此外，還存在“主觀”或是“證據性”的觀點。這一派認為概率因人而異，反映了每個人對於什麼為真，或是什麼會發生的置信程度差異。貝葉斯學派就是這樣的例子。該學派的核心為貝葉斯定理。在獲得新信息時，這一數學定理闡述瞭如何調整我們對不同可能性的置信程度。在貝葉斯學派的構想中，處於信息不全面處境下的理性生物會對所有可能結果的置信程度進行評估，並根據新數據逐漸調整它們。和頻率學派形成鮮明對比的是，貝葉斯學派可以給無法重複的事件（如下次大選誰會獲勝）分配概率，甚至能估計我們不確定的過去事件概率。

三種當下最廣為接受的量子理論。首先是吉安卡洛·吉安爾迪（Giancarlo Ghirardi）、阿爾博託·裏米尼（Alberto Rimini）和圖利奧·韋伯（Tullio Weber）在1985年提出的“動力坍縮”理論。然後是各種“導航波”或“隱變量”理論，其中最有名的即戴維·波姆（David Bohm)在1952年根據路易·德布羅意（Louis de Broglie）早先想法創造出來的德布羅意-波姆定理。最後還有休·艾弗雷特（Hugh Everett）在1957年提出的“多世界”詮釋。

這三種理論各自代表了一種解決量子力學測量問題的方法。在傳統量子理論中，系統的狀態以波函數表示。只要沒有觀測者，波函數將根據薛定諤方程平滑地確定性演化。一旦發生觀測事件，物理課本中經常將其描述為波函數突然“坍縮”成某一觀測結果。坍縮本身的結果是隨機的，波函數會給每種可能發生的結果分配數值，觀測到該結果的概率等於相應波函數幅值的平方。因此，所謂的量子測量問題即：什麼事件能被稱為“測量”？它發生的精確時刻是怎麼確定的？為什麼測量事件會和系統的正常演化不同？

六．復變概率和復變信息論的探索

6.1）概率與信息論的關係

概率是信息論中信息度量的基礎。根據香農的信息定義，信息是對事物運動狀態或存在方式的不確定性的描述。而不確定性可以通過概率來表示，因此概率為信息的量化提供了依據。例如，對於一個離散的隨機變量，其每個取值的概率分佈決定了該隨機變量所包含的信息量。如果一個隨機變量的取值非常確定，即某個取值的概率接近 1，那麼它所包含的信息量就很小；反之，如果隨機變量的取值非常不確定，每個取值的概率都比較接近，那麼它所包含的信息量就很大。

以上這些內容都摘抄網絡上相關比較正式資料的內容，避免相關專業詞彙定義的偏差。

6.2）概率可以是複數嗎？

前面的所有引用資料都説明一個事實，人們把概率定義成一個0-1之間的實數 。從純粹數學角度來看，任何一個實數都可以表示成為一個複數，只是這個特別複數的虛部永遠是零，為了便於書寫變量就不寫成複數形式。同樣我們也可以將 概率定義成模在0-1之間的複數，從數學上沒有任何障礙。

當概率定義為一個複數時，就比定義為實數的概率多個一個虛部值或者相位值。當這虛部值或者相位值不等於零時，我們可以嘗試探索更多的性質。

同樣，基於實數概率的香濃信息熵的定義也可以用複數概率來重新定義，獲得複數信息熵，同樣比實數信息熵多出了一個相位熵。

我們的研究初步完成了複數香濃熵的推導和相關幾個基本復變香濃熵的屬性的推導。

我認為，實數概率和實數香濃熵是在物理學牛頓力學座標系中的主觀性效果。其物理基礎來自不科學觀察方式的人眼觀察效果，自然帶有主觀性。量子力學的量子概率是基於科學儀器的科學測試效果，才是真實世界的客觀概率效果。複數概率是將量子概率的理念推廣到我們日常的牛頓力學物理世界座標系環境，還原了真實牛頓力學環境中的概率定義和公式的本質。

同樣道理，複數香濃熵是將量子信息熵概念推廣到人類日常的牛頓力學座標系空間，體現了真實的信息熵的本質。從而統一了量子概率和實數概率，量子信息熵與香濃熵的數學公式表達。

6.3）複數香濃熵應用場景推測

我們推導複數香濃熵公式如下：

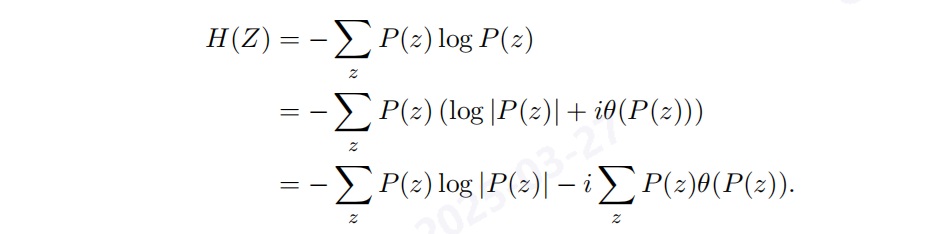
複數概率和複數香濃熵的相位值可以帶給我們很多應用場景。

例如，在當前最熱門的Transformer 注意力機制中，除了單詞嵌入值還有位置嵌入值，而位置嵌入值是一個固定或者動態的三角函數值 ，從複數信息熵的角度來看，兩個概率分佈的交叉熵，除了對比實數概率，還需要對比相位概率，自然會引入位置嵌入參數。

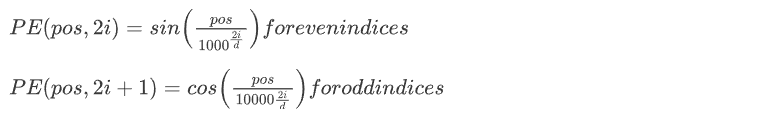
同樣在量子力學中，除了矩陣力學形式和波動力學形式外，路徑積分形式就是基於量子概率，路徑積分的形式中自帶相位值，我認為這也是複數概率的本質決定的。複數概率和複數信息熵可以給路徑積分一個新的理解思路。

由於複數概率本身的幾何特徵，對複數概率和複數信息論可以採用現代復幾何的數學工具來更加全面的研究和擴展。

關於復變香濃熵的內容歡迎查看我們論文：

鏈接[[2503.03759] Information entropy of complex probability](https://arxiv.org/abs/2503.03759)