另類三體：如果月球軌道換個方向，就會撞上地球 | 袁嵐峯_風聞

牛頓因為疫情的原因，躲在鄉下思考天地日月星辰，終於領悟了萬有引力的原理。他把這個天地大道藏在心裏，直到有一天，哈雷來看望他。

牛頓看見哈雷，就上了山，既已坐下，哈雷到他跟前來。他就開口教訓他，説：

枝頭的蘋果落地了，因為地球是吸引它的。

扔出去的石子會落地，也是因為地球吸引它。

站在山上扔出去的石子，落地的位置更遠，因為地球吸引它下落的距離變大了。

站在山上扔出去的石子，出手時的速度越快，落地的位置就越遠，因為地球吸引它落地的這段時間裏，石子飛躍的距離變大了。

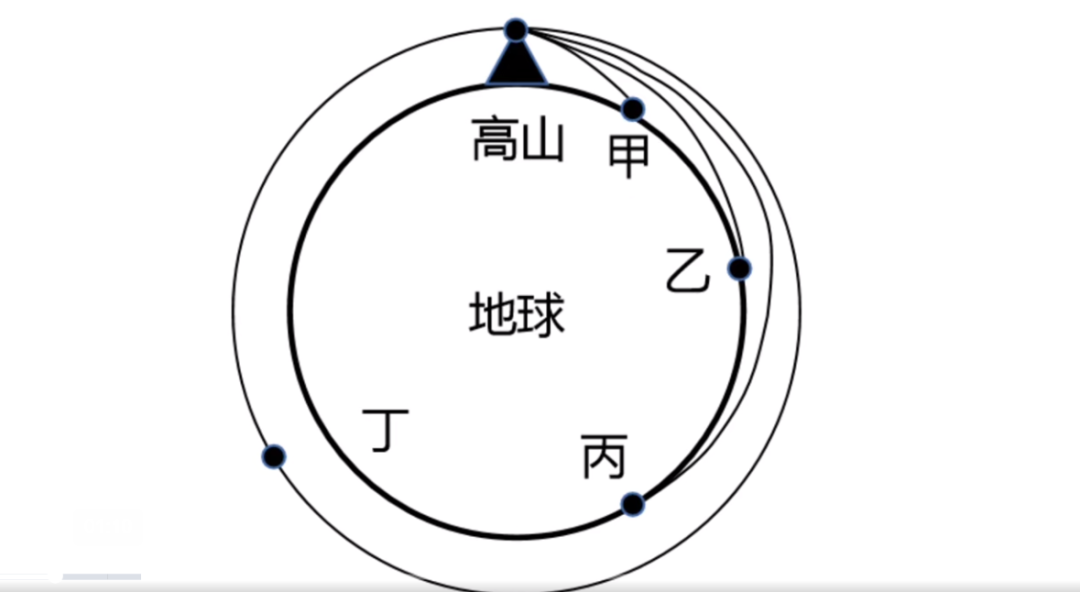
只要石子出手的速度足夠快，就不會落到地面上，因為地球是圓的，石子在地球的吸引下不停地下落，而地面也在不停地向下彎曲。所以，石子永遠不會落到地面上，這就是人造衞星。

地球對石子的引力符合平方反比定律，球體的引力就像所有質量集中在地心一樣。只要石子的速度不是特別快，它就會回到我這裏，因為石子的運行軌道是橢圓。

月亮繞着地球轉，地球繞着太陽轉，都是這個原因。世間的萬物相互之間都有引力作用，都符合平方反比定律。由此可以揭示宇宙的奧秘。

牛頓講完了這些話，哈雷很稀奇他的教訓。因為他教訓他，正像有權威的真科，不像偽科學的網紅。

以上這段牛頓的“登山寶訓”，是誰寫的？是我的科大師兄、曾任中國科學院半導體研究所研究員、現任浙江大學物理學院教授的姬揚老師。姬揚老師一向充滿幽默感，十分熱愛科普和翻譯。他2022年在我的科普平台“風雲之聲”發了一篇文章《另類三體：如果月球軌道換個方向，就會撞上地球 | 姬揚》，開頭就是這個牛頓的登山寶訓。

咦，這個標題是什麼意思？如果月球軌道換個方向，就會撞上地球？是的，這才是姬揚老師這篇文章的主旨。他從1987年在中國科學技術大學物理系讀書以來，學了30多年物理，還教了好幾年物理，但直到2021年讀了一本書，才知道竟然還有這麼一件事。這本書就是俄國著名數學家阿諾德的回憶錄《昨日和往昔》（Vladimir I. Arnold, Yesterday and long ago, Translated by Leonora P. Kotova and Owen L. deLange, Springer, 2007）。

下面借用阿諾德的描述。蘇聯科學家利多夫（Michail L’vovich Lidov, 1926 - 1993）在1960年提出並回答了這樣的問題：我們知道，太陽、地球和月球基本是在一個平面上，地球繞太陽公轉的軌道平面（即黃道面）和月球繞地球公轉的軌道平面（即白道面）的夾角只有大約5度，這是一個相當穩定的三體系統。然而，如果我們把月球豎起來，也就是説，讓白道面和黃道面垂直，日地月這個三體系統還會這麼穩定嗎？

我們可以看圖來仔細理解一下這個問題。地球繞太陽公轉的軌道平面叫黃道面（即圖中藍色的大圓），月球繞地球公轉的軌道平面叫白道面（即圖中桔色的小圓），二者的夾角只有大約5度，也就是説，它們基本都位於屏幕所在的平面上。

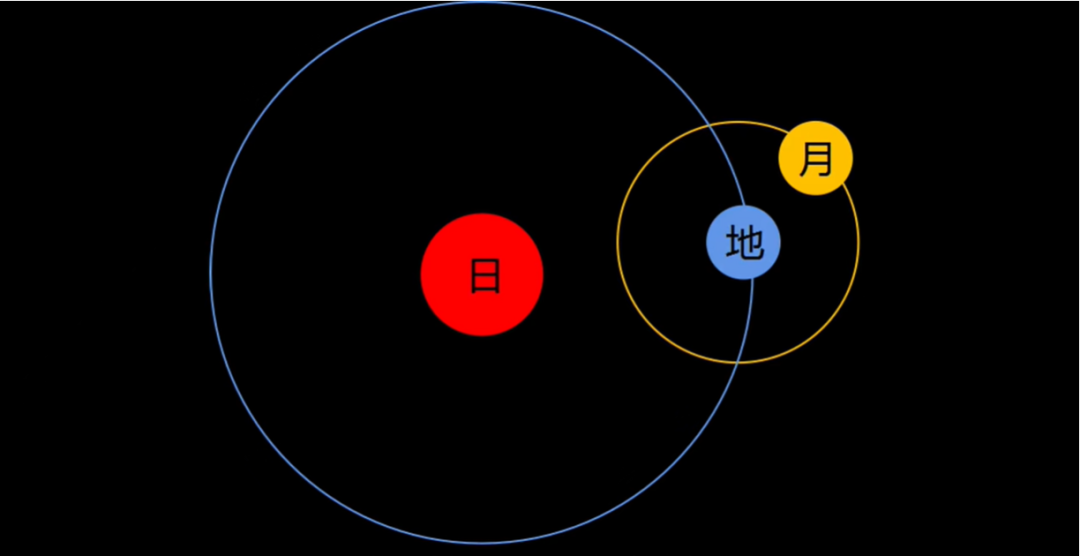
利多夫的問題是：如果我們把桔色的這個小圓豎起來，讓它跟屏幕垂直，三體系統還會穩定嗎？

實際上，利多夫的問題比這個簡單描述要普遍得多，被稱為圓形限制性三體問題（Circular Restricted Three Body Problem，簡稱CR3BP）。他用了很多數學技術（久期近似的雙週期平均）以及當時剛出現不久的計算機，得到了相當普適的結果，後來被稱為Kozai-Lidov 機制。Kozai是日本科學家古在由秀（Yoshihide Kozai，1928–2018），他當時在美國史密斯天文台工作，知道Lidov的工作，隨後也發表了自己的工作。

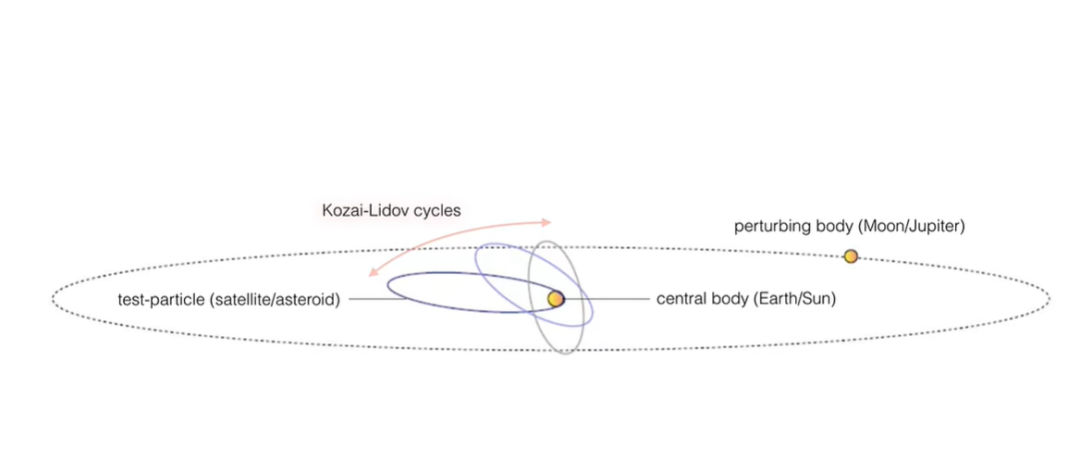
這個問題如果用解微分方程的辦法來處理是很困難的，列出適當的微分方程就不容易，而且最終也要求助於數值解法。但幸運的是，現在隨便一個台式機都比當年的超級計算機強大得多，還有很多科學計算軟件幫助我們做數值運算。下面我們用一個簡單的模型以及Scilab給出的計算結果，來説明問題。

在日地月系統中，因為太陽質量 >> 地球質量 >> 月球質量，可以簡單認為，太陽不受地球和月球的影響，地球不受月球的影響。所以只需要考慮月球繞地球的轉動，包括地月引力的作用以及日月引力（扣除月球繞太陽公轉所需的向心力部分以後）的殘餘影響。地球的公轉決定了一個平面也就是黃道面，選擇月球的初始速度（大小和方向），可以確定其初始的軌道面以及相對於黃道面的夾角。下面只考慮這個夾角為0度和90度的情況。選擇月球的初始軌道為一個偏心率百分之幾的橢圓，類似於真實世界的月球。

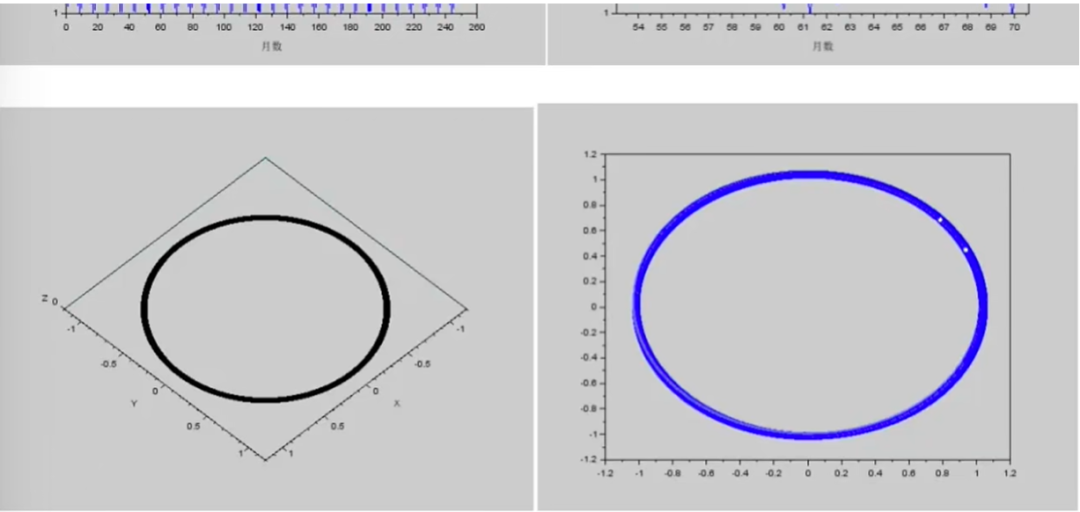
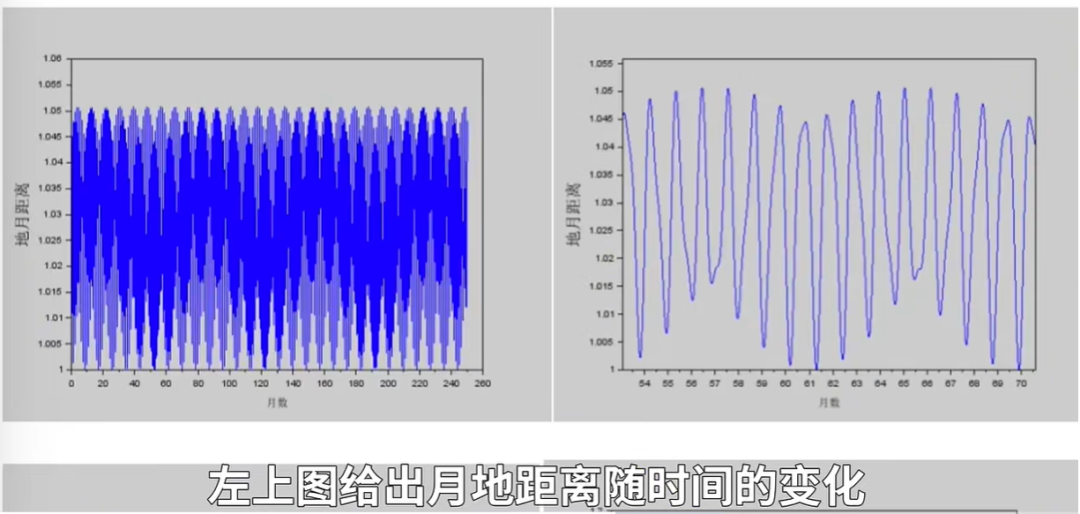
首先來看0度的情況：人生代代無窮已，江月年年只相似。月球軌道保持在黃道面內，是進動的橢圓，因為所有的力都在這個平面內，太陽的擾動引起了進動。左上圖給出月地距離隨時間的變化（右上圖是局部的放大圖），顯然它的變化不大。這裏的1指的是真實的地月距離38萬公里，從圖中可以看出，對它的偏差從來沒有超過5%。相鄰兩個近地點的時間，就是一個月。200多個月的軌道疊在一起，看着就像一個圓（左下）。在50 - 60個月之間選了幾個月的軌道，疊在一起仍然像一個圓（右下）。

再來看90度的情況：月亮撞地球，天地大劫難。左上圖給出地月距離隨時間的變化（右上圖是局部的放大圖），可以看到它的變化幅度非常大。在50多個月的時間裏，就從正常距離變到這個值的1 - 2%左右，即3800公里至7600公里。請注意，地球半徑是6400公里，月球半徑是1700公里，兩者加起來是8100公里，所以7600公里的地月距離意味着月球已經撞上了地球！

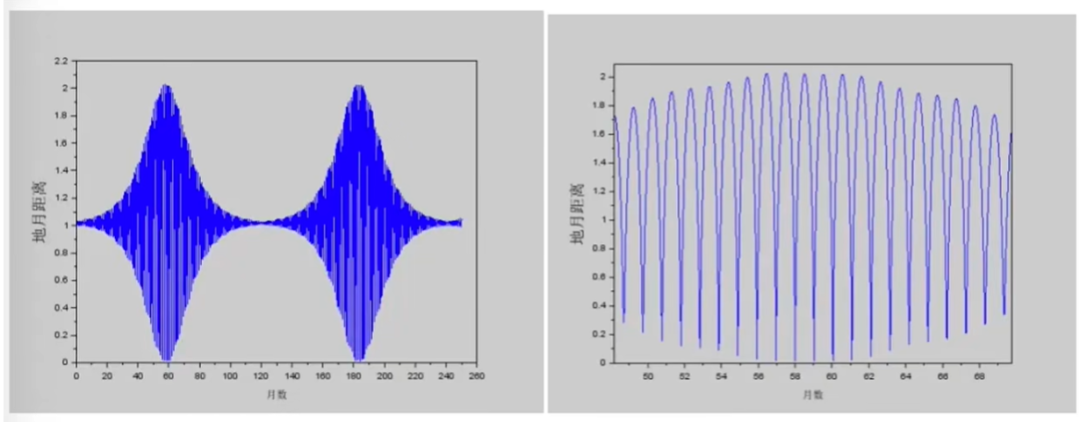
為什麼計算在地月相撞之後還沒停止呢？因為它用的是質點模型，即認為月球和地球都只是一個點。所以在距離達到極小之後，居然又回去了，最大接近正常值的兩倍。但這都不現實了，在第一次相撞之後，地月系統就會毀滅。

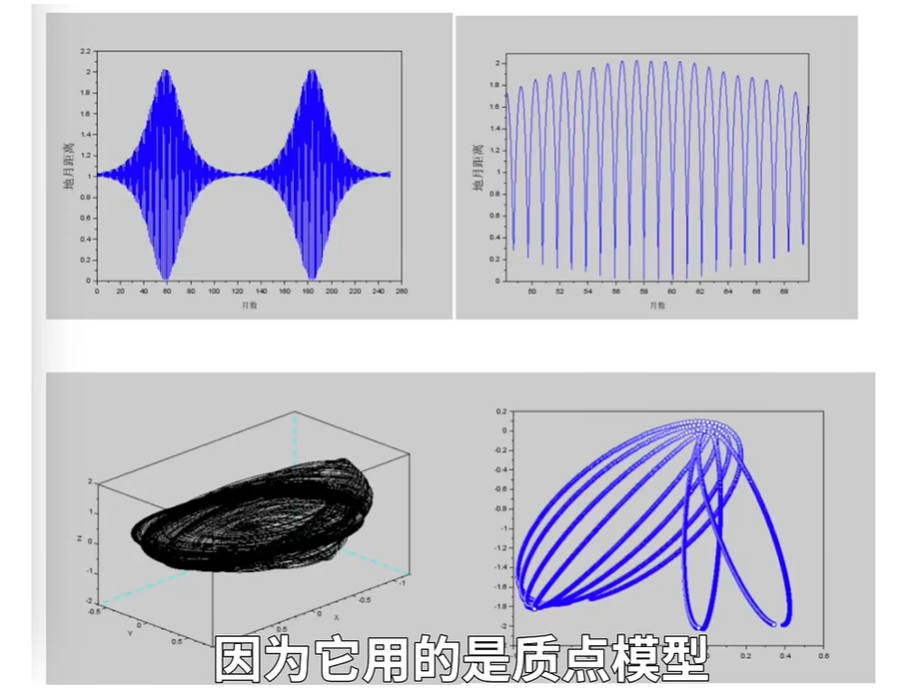
所以結論是，把黃道面與白道面的夾角從0度變成90度，就會在5年內導致世界毀滅，我們有幸觀測到比恐龍在6500萬年前看到的更大的焰火。不過這只是數值計算的結果，更深入的問題是，為什麼會有這樣的結果呢？

我們可以畫一個比例有點誇張的三體系統示意圖來説明。

地球（黑點）繞着太陽（紅點）的公轉軌道是圓形的細黑線，月球繞地球公轉的軌道是橢圓的粗黑線，太陽對月球的微擾力（即扣除了萬有引力中讓月球繞太陽公轉的那部分貢獻）的方向在地球公轉軌道即細黑線以內是朝向太陽的，在細黑線以外是遠離太陽的。這個微擾讓月球軌道變形，併發生進動。

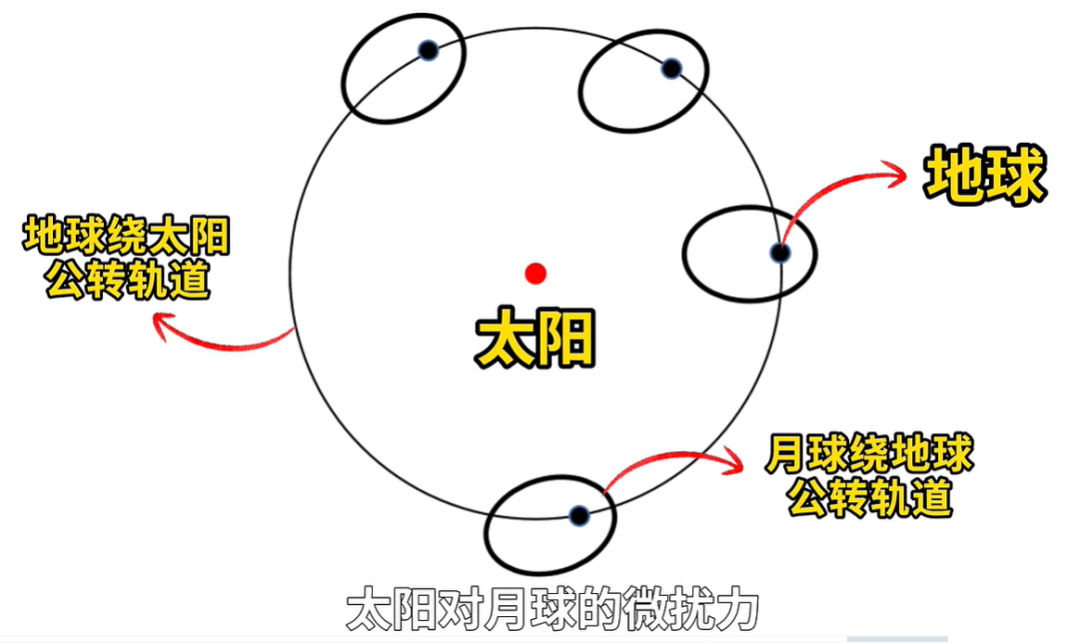
在0度的情況，月球軌道與地球軌道在同一個平面內，地球繞太陽的轉動和月球軌道的進動使得這個橢圓的變形不會越來越大。太陽微擾導致的變形是隨時間變化地揉搓這個橢圓，整體效果是讓月球軌道大致保持初始的形狀。

在90度的情況，月球軌道垂直於地球軌道，地球繞太陽的轉動只能改變太陽微擾在月球軌道上的投影大小，但是方向不變。變形的效果就可以累加起來，讓這個軌道越來越扁，最終撞到地球上。

當然，這個解釋還很粗糙。比如説，沒有考慮我們剛才的計算模型裏地球座標系是非慣性系（因為它繞着太陽轉動）。這個三體系統還有很複雜的行為，但這就超出本文的範圍了。

再讓我們回到牛頓的登山寶訓。如果地球是完美的球體，周圍沒有大氣的阻礙，只考慮月球的影響，那麼，牛頓在山頂高速扔出去的那個石子，真的會變成一顆人造衞星，永遠繞着地球轉動嗎？ 

現在你明白思路了吧？現在的石子、月球、地球就好比剛才的月球、地球、太陽。

所以答案是：這取決於牛頓朝哪個方向扔石子！如果朝東西方向扔，它就會一直轉下去。而如果朝南北方向扔，它就會在不長的時間內，撞到大地母親的懷抱裏！

最後，你也許想問，這個效應有多普遍？答案是相當普遍，這種圓形限制性三體問題（CR3BP）在許多場合都會出現。

牛頓沒有提出這樣的問題，是因為當時的天文觀測只能看到很有限的星空。而利多夫提出這個問題，是因為蘇聯發射了人造衞星，精確確定衞星軌道隨時間的變化是非常重要的科學問題，計算機的發展提供瞭解決這個問題的機會。這就是為什麼，這個問題以及它的解答出現在僅僅60多年前，在蘇聯發射第一顆人造衞星“斯普特尼克”之後，在牛頓逃到鄉下悟道300年之後。