龐加萊的數學交響:自守函數動機在20世紀的變奏與展開_風聞
返朴-返朴官方账号-关注返朴(ID:fanpu2019),阅读更多!8分钟前

龐加萊對自守函數的研究促使分析、幾何、代數等領域進一步統一,奏響了19世紀末數學的華彩樂章(參見《19世紀末的數學高峯:龐加萊的自守函數研究》)。這一理論作為核心“動機”,更是在20世紀數學的宏大交響中展開了波瀾壯闊的“變奏”:從世紀初的單值化定理到費馬大定理和朗蘭茲綱領,再到多複變函數與低維拓撲學的研究,自守函數孕育的思想超越了古典形式,持續迸發活力。龐加萊的智慧光芒,始終在人類宏大的知識圖景中閃耀。
撰文 | 金威
經由前文《19世紀末的數學高峯:龐加萊的自守函數研究》,我們重温了龐加萊(Henri Poincaré,1854-1912)在自守函數領域的創造性突破。龐加萊和克萊因(Felix Klein,1849-1925)的自守函數研究,在19世紀末一統分析、代數和幾何等數學幾大領域,展現了數學在多樣性背後的統一性(參考文獻見[1]-[15])。而在此基礎上,又湧現出諸多豐富多彩的問題和理論。
在此文中,筆者將不揣淺陋,初步地梳理和介紹其中的幾個有代表性的方向。由此管中窺豹,我們可以欣賞到如下的圖景。首先,在龐加萊的數學交響曲中,自守函數這一核心“動機”在20世紀初的單值化定理中完成初步的展開。此後,它並未止步於古典形式,而是通過現代數學的復調演繹——從數論中神秘的千古之謎(費馬大定理)和大統一(朗蘭茲)綱領,到多複變函數論和數學物理中的迷人應用,再到三維流形理論中拓撲與幾何的對位共鳴——不斷獲得新的演進維度。
正如音樂動機在不同樂章中的變奏與再生,自守函數“動機”在20世紀數學的各個領域中持續演繹發展並多重奏鳴,呈現出理論數學優美而宏偉的時空結構。
1
自守函數理論“大統一”的尾聲:單值化定理

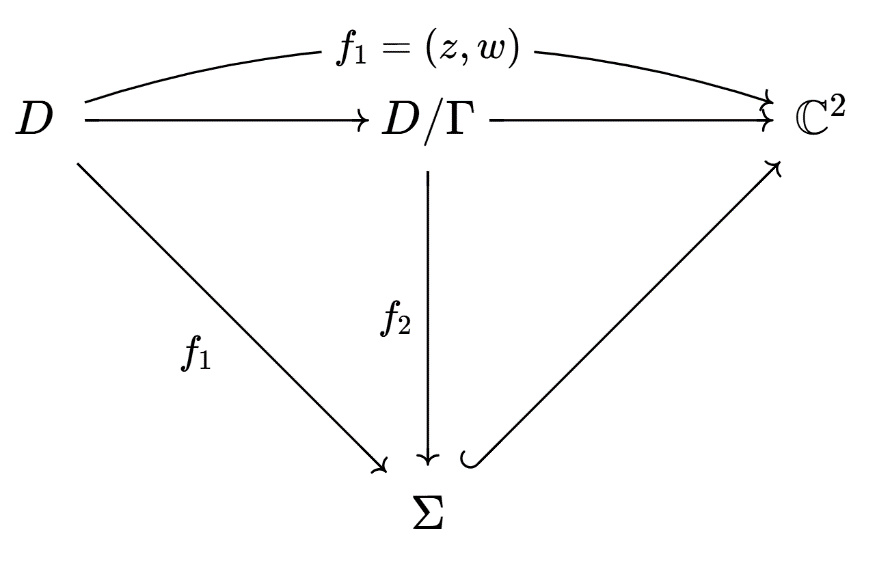
圖1
在這種參數化的意義下,根據當時熟知的結論和龐加萊、克萊因等人的工作,對代數函數的黎曼面Σ,如果其虧格為0,則可以用有理函數單值化;如果虧格為1,則可以用橢圓函數單值化;如果虧格大於等於2,則可以用自守函數單值化。

龐加萊和寇貝(Paul Koebe,1882-1945)在1907年證明了單連通情形下的單值化定理:

這解決了單變量下的希爾伯特第二十二問題:“用自守函數將解析函數單值化”。
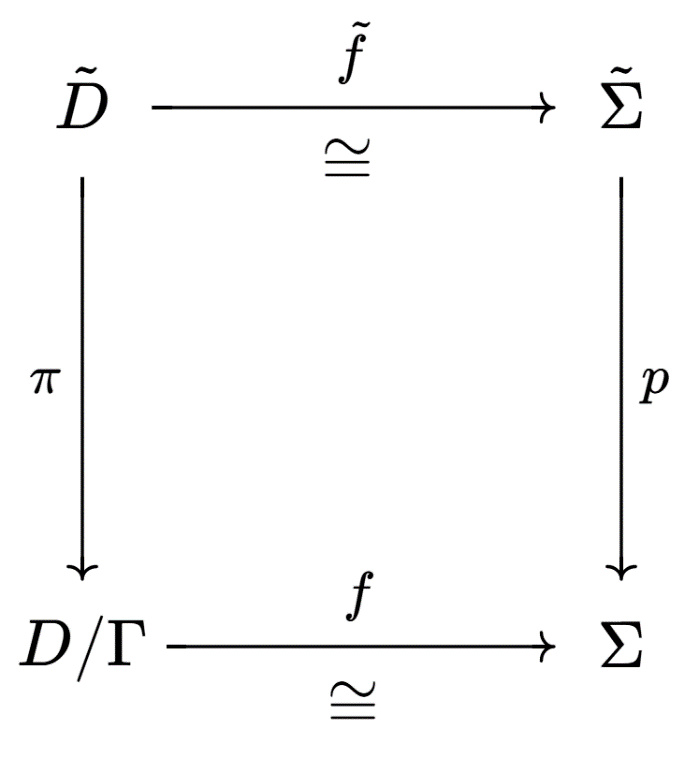
圖2


建立單值化定理,是單複分析理論的一個高峯,它進一步統一了數學中的分析、代數、幾何、拓撲幾大領域(並可兼涉數論),見圖3。然而,在歷史上,以上陳述中所涉及的抽象黎曼曲面的定義,其實比單值化定理本身出現得更晚:它是由外爾(Hermann Weyl,1885-1955)在寇貝工作的基礎上,在《黎曼曲面的概念》(1913)一書中給出的。
根據拓撲學中的曲面分類定理,任何緊可定向曲面都同胚於有限虧格、有限個邊界的閉曲面。而單值化定理實際上指出:如果考慮復結構,則任意(有限類型的)復曲線不僅是同

在幾何觀點下,這三類“標準復空間”分別可以賦予球面幾何、歐氏(平面)幾何和雙曲幾何,這三種幾何都是“全局對稱的”,被稱為齊性幾何,它們分別具有常曲率+1、0、-1。這就把所有的閉可定向曲面賦予了幾何結構,並從幾何上將它們分成了三大類:球面,具有球幾何;環面,具有歐氏幾何;虧格大於等於2的曲面,具有雙曲幾何。如果去掉“閉”條件,而改為具有有限個邊界並挖掉有限個點的曲面,結論依然成立。並且,在這三種齊性幾何結構中,雙曲結構是最普遍(如果等概率地隨機選取虧格、邊界和所挖掉的點的數目,則所選出的曲面有雙曲結構的概率為1)而又最複雜的。
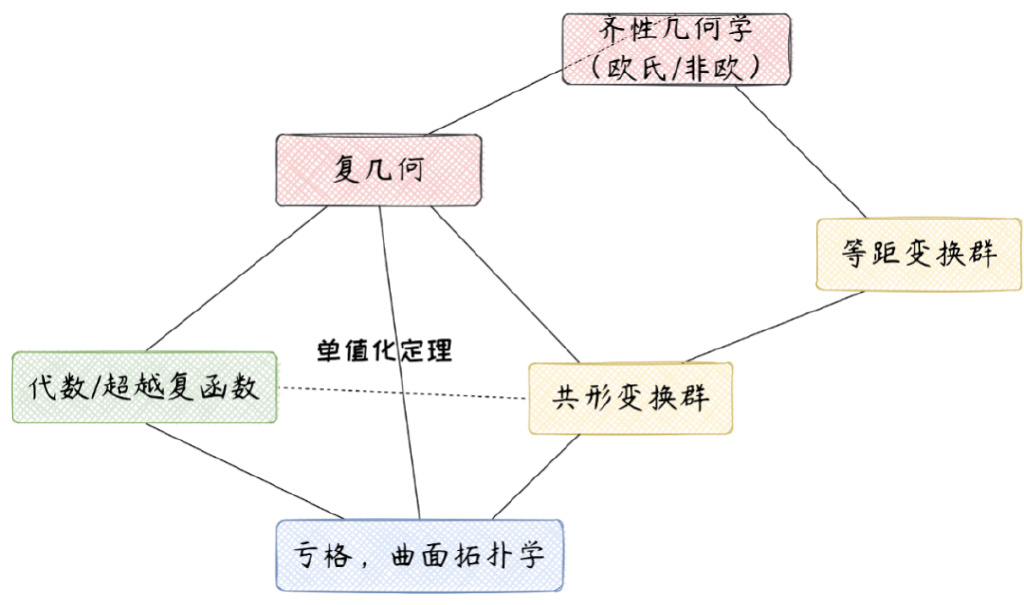
圖3 不同顏色表示不同領域:紅色—幾何;黃色—代數;藍色—拓撲;綠色—分析,下同。
數學家們自然地提出瞭如下問題:
在更高維數下,還有與之類似的情況嗎?
在第三部分我們將會看到,在三維世界中,仍然可以有類似的聯繫,而且在相當長的時間內,雙曲幾何和克萊因羣的理論是三維流形拓撲學的主要工具之一。
證明單值化定理,除對代數函數情形可以使用自守函數理論證明之外,對一般情形大都需要用到分析學中的工具,如(嚴格化之後的)狄裏克萊原理等,後來又陸續發展出Perron方法和熱核方法等。相關證明可參考黎曼曲面方面的著作。
2
數論中的自守函數——費馬大定理與朗蘭茲綱領
在數論方面,經過之後百餘年的發展,自守函數和自守形式已成為數論學家必備的常用工具。此處先以費馬大定理為例做一展示。
在1637年前後,法國職業律師、業餘數學家費馬(Pierre de Fermat,1601-1665)在丟番圖的《算術》一書頁邊上陳述了定理:當𝑛 ≥ 2時,方程𝑥^𝑛 + 𝑦^𝑛 = 𝑧^𝑛沒有正整數解,而其證明則因“空白太窄,寫不下”,此後兩百年間數學家對其進行了很多嘗試,在19世紀上半葉之前,費馬本人、歐拉(Leonhard Euler,1707-1783)、熱爾曼(Sophie Germain,1776-1831)、狄裏克萊(Lejeune Dirichlet,1805-1859)、拉梅(Gabriel Lamé,1795-1870)、庫默爾(Ernst Kummer,1810-1893)等人證明了許多特殊情況。1983年法爾廷斯(Gerd Faltings,1954-)證明了莫德爾猜想,其一個推論就是給定次數下此方程的(本原)整數解只能有有限多組,該工作也使得數學家對證明費馬大定理抱有更大希望,而且將目光更多聚焦在幾何方法上。
隨着數論的發展,谷山豐(Taniyama Taniyama,1927-1958)—志村五郎(Goro Shimura,1930-2019)在20世紀五十年代從具體計算出發,和之後的韋伊(André Weil,1906-1998)先後提出了谷山-志村-韋伊猜想,指出有理數域上的任何橢圓曲線都是模曲線,或者説是“被模形式參數化”。

的無窮遠點處全純),其中的整數𝑘稱為模形式的“權”。我們曾在上文見到過這個條件,其中權為0的亞純模形式就是經典的模函數。而所謂一條(有理數域上的)橢圓曲線𝐸: 𝑦^2 = 𝑎𝑥^3 + 𝑏𝑥^2 + 𝑐𝑥 + 𝑑被模曲線參數化,其陳述形式之一是存在權相同的模曲線𝑓(𝑧)和𝑔(𝑧),使得:𝑔(𝑧)^2 = 𝑎𝑓(𝑧)^3 + 𝑏𝑓(𝑧)^2 + 𝑐𝑓(𝑧) + 𝑑,這等價於橢圓曲線𝐸與該模函數具有相同的狄裏克萊𝐿級數展開。讀者可以看到,此處的“參數化“實質上又是上文中的”單值化”。
之後,弗雷(Gerhard Frey,1944-)首先將任意次數的費馬方程關聯到橢圓曲線,指出:如果𝑥^𝑛 + 𝑦^𝑛 = 𝑧^𝑛有正整數解(𝑎, 𝑏, 𝑐),那麼考慮橢圓曲線𝐸: 𝑦^2 = 𝑥(𝑥 − 𝑎^𝑝)(𝑥 + 𝑏^𝑝),它不能被模曲線參數化。在1984年弗雷宣佈此消息時,聽者無不歡欣鼓舞,不過當時在證明中存在一些邏輯漏洞,後在1986年由裏貝特(Ken Ribet,1948-)和塞爾(Jean-Pierre Serre,1926-)彌補。當時羣情激奮的原因是,弗雷的陳述實際是在説——谷山—志村—韋伊猜想藴含費馬大定理!
最後,自小懷揣天真夢想,在青年時期就已在數論領域名聲大噪的劍橋的懷爾斯(Andrew Wiles,1953-),經過“面壁”七年並屢遭挫折後,藉助代數數論中更加深刻的工具,終於在1995年證明了(半穩定情形下的)谷山-志村-韋伊猜想,並由此宣告證明了費馬大定理。在這七年之中,他每半年左右發表一篇小論文以“掩人耳目”,並直至證明完成前夕的1994年,仍因錯誤尚未完全排除而面臨着巨大壓力。
以上歷史過程的大致路線圖如下。
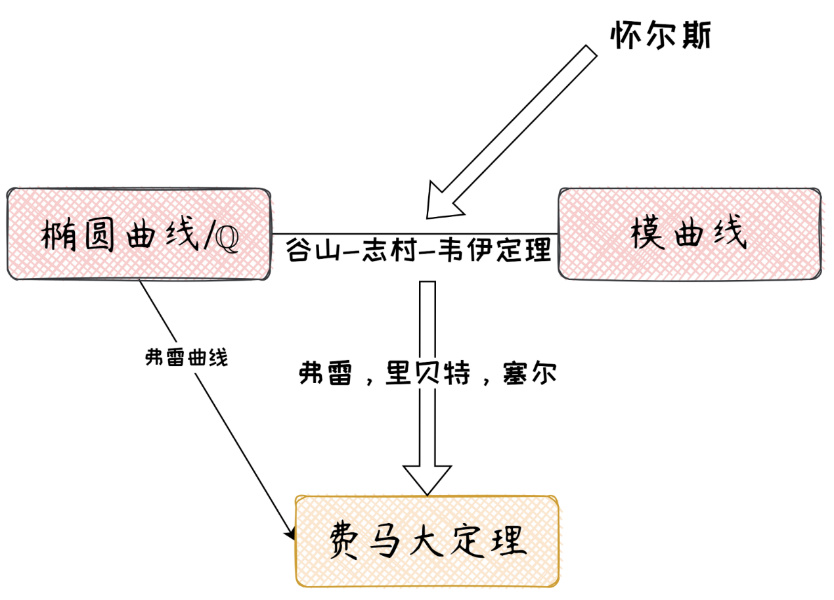
圖4
值得注意的是,費馬大定理與自守函數理論的關聯是雙重的。一方面,橢圓曲線實際上就是橢圓函數的黎曼面,而複數域上的橢圓曲線/橢圓函數也是自守函數的經典實例之一(參見《19世紀末的數學高峯:龐加萊的自守函數研究》序曲1.1節),當然在這個問題中考慮的是有理數域(而不是複數域)上的橢圓曲線;另一方面,模曲線則是自守函數的推廣,而它所符合的代數性質正是龐加萊在構造富克斯函數時所考慮過的“模性”。
費馬大定理是著名的“朗蘭茲綱領”所揭示的更廣闊圖景的一部分。首先,根據軌道-穩定子

分析學(如調和分析)所研究的對象。由此可見,自守表示是自守函數的推廣。而朗蘭茲綱領指出,來源於數論、分析、(代數)幾何的三種對象:伽羅瓦表示、自守表示和代數簇的上同調理論,在本質上是統一的[體現為阿廷𝐿函數、自守𝐿函數和哈塞(Hasse)—韋伊𝐿函數的統一性]。它被稱為數學的“大統一理論”。
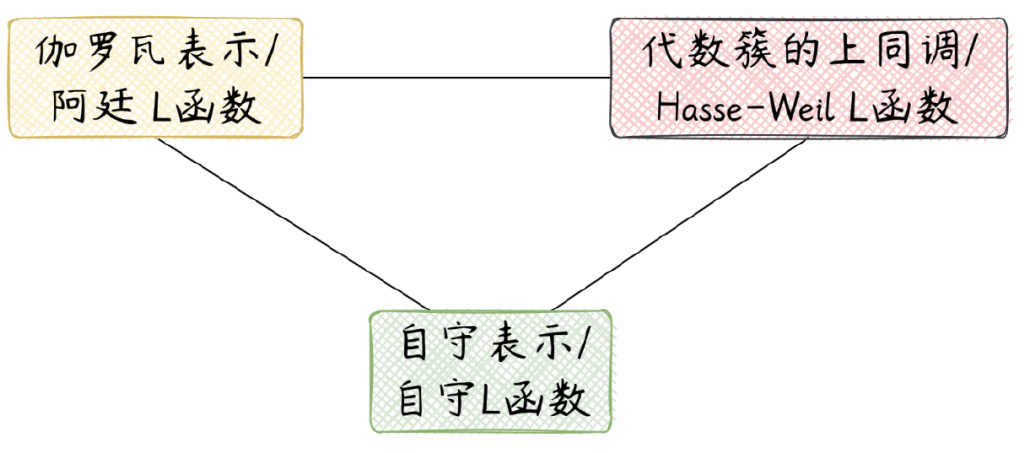
圖5
3
自守函數在多複變函數理論中的推廣與應用略談
龐加萊經過一系列的數學發現,事實上和之後的庫辛(Pierre Cousin,1867-1933)、哈託格斯(Friedrich Hartogs,1874-1943)等人開創了多複變函數這個數學領域。尤其是

間不成立,這也説明在多複變函數領域中沒有與單復變中單位圓完全相當的區域;與之最相近的區域稱為“典型域”,是不可分解對稱有界域在全純等價下分類的標準域。
此後,我國數學家華羅庚(1910-1985)嘗試將單複變函數中的自守函數推廣到多複變函數論領域。他的代表作之一為《多複變函數論中典型域上的調和分析》,並由此在1956年獲得我國國家自然科學獎一等獎(當時稱為“中國科學院科學獎金”)。他的研究始於上世紀40年代西南聯大的艱苦時期。同時,德國數學家西格爾(Carl Siegel,1896-1981)也在研究有界對稱域及其幾何,他們的研究對馮康(1920-1993)等在辛算法的工作也有重要影響。華羅庚後於1946年在《數學年刊》上發表《多複變函數的自守函數》,成為該領域經典文獻。華羅庚於1950年放棄美國的優厚待遇毅然回到新中國,在回國初期,他的研究轉入多複變函數典型域上的調和分析,用羣表示理論具體構造了典型域上的平方可積全純函數的完備正交基,並做了很多具體計算,這也使得調和分析領域在60年代變得更加熱門。丘成桐(1949-)教授對此的評價是:“(華羅庚教授)在多複變函數方面的貢獻比西方至少早了十年。” 華羅庚教授研究的特色是從特殊到一般、從具體到抽象、從簡單到複雜,並重視例子和具體計算(包括對矩陣的大量計算)。
華羅庚在典型域上的自守函數和調和分析的研究,還應用到微分方程、數學物理等領域,形成了“華羅庚學派”。我國的陸啓鏗(1927-2015)、龔昇(1930-2011)、郭漢英(1939-2010)、周向宇(1965-)等學者的研究都受到其很大影響,或與之聯繫緊密。華羅庚還曾用矩陣方法處理狄拉克算子及其熱核自守形式等,它們是後來的指標定理、Seiberg-Witten方程等理論的基礎,由此可見華老不凡的學術洞察力。
此外,我國數學家李國平(1910-1996)在20世紀50年代訪問蘇聯科學院後,大大發展了法國數學家當茹瓦(Arnaud Denjoy,1884-1974)的工作,與合作者在黎曼—龐加萊的幾何觀點的基礎上系統地發展了常微分方程的解析理論,並將閔可夫斯基函數和自守函數推廣到巴納赫空間上(即“泛函化”,其核心思想是利用龐加萊之前的級數展開進行推廣),而且將其用於研究廣義積分論、連續介質力學和量子場論等領域,從而推廣了蘇聯穆斯赫利什維利(Никола́й Ива́нович Мусхелишви́ли,1891-1976)學派的相關工作。這是在分析領域,龐加萊自守函數工作的另一變奏與迴響。(可參見[16][22])
4
自守函數“大一統”的三維版本與低維拓撲學的發展
在二維世界中,由於單值化定理和高斯-博內定理等,曲面為代數-球幾何/歐氏幾何/雙曲幾何—復幾何—拓撲這幾種觀點提供了共同的舞台,它們在此處交相輝映,五光十色。拓撲學家嘗試將這種二維的美妙情景推廣到高維。同時,龐加萊本人也是三維流形拓撲學和代數拓撲學的早期開創者。由此,現在數學家要解決的問題是:
(1)以上的二維結果如何推廣到三維?
(2)在三維情況下,羣與流形——具有某種幾何的萬有覆蓋空間的商流形的關係?
(3)二維情況與三維情況的聯繫?
在此方面,瑟斯頓(William Thurston,1946-2012)可以看作將龐加萊的思想從多個角度全面進行了推廣。我們簡述其貢獻中的幾個方面。
第一個方面與泰希米勒(Oswald Teichmüller,1913-1943)空間相關。所謂泰希米勒空間,是指在給定虧格的曲面上,所有“帶標記的”復結構或雙曲結構(的同痕類)構成的空

瑟斯頓考察了泰希米勒空間的球面邊界,證明其邊界上的點可以視為原雙曲曲面上的一種有時十分複雜的曲線 [即所謂“賦測度片層” (measured lamination)],由此可以將泰希米勒空間緊化。之後他將此觀點用於研究映射類羣(mapping class group),並以此證明了曲面自映射的尼爾森(Jakob Nielsen, 1890-1959)—瑟斯頓分類定理。該定理指出曲面自映射分為三類,分別為週期的、可約的和偽阿諾索夫 (pseudo Anosov) 的,其中偽阿諾索夫映射在三維流形理論中扮演了重要角色。他還用雙曲幾何觀點定義了泰希米勒空間上的度量,後來沃爾珀特(Scott A. Wolpert)證明與韋伊-彼得森(Weil-Petersson)度量一致(1986)。
第二個方面是所謂幾何化定理,它可以被直接地看成單值化定理的直接三維推廣。首先,安德烈耶夫(E. M. Andreev)在1970年給出了用鋭角四面體剖分給出有限體積雙曲流形的方式。此後萊利(Robert Riley,1935-2000)和約根森(Troels Jørgonsen)在1975

在這些工作的基礎上,瑟斯頓用四面體剖分具體構造了八字結補空間上的完備雙曲結構
(1979年),並由此猜測雙曲結構在三維流形中是普遍存在的,並在20世紀70-80年代分別證明在大部分紐結(即非環面、非衞星紐結)的補空間和由偽阿諾索夫映射誘導的圓周的曲面叢上,都有完備且有限體積的雙曲結構。進一步地,他提出了一系列猜想,其中最重要的是所謂的幾何化猜想,即每個閉的素三維流形都可以沿環面(唯一地)切開成一些塊,使得每塊上有(有限體積的)八種齊性幾何之一。這八種幾何是二維情形下三種齊性幾何的類似物,包括球幾何、歐氏幾何、雙曲幾何的三維版本、或其低維版本的乘積,此外還有三種來自於李羣。
我們注意到,幾何化定理不僅可以看作是單值化定理的三維版本,而且包含三維龐加萊猜想作為其推論。對所謂哈肯(Wolfgang Haken,1928-2022)流形,瑟斯頓在1980年代證明了幾何化猜想。而對一般的三維流形,證明則由佩雷爾曼(Григо́рий Я́ковлевич Перельма́н,1966-)利用裏奇流(Ricci flow)技術在2003年完成,並因此獲得菲爾茲獎(但拒領)。此外,正如龐加萊用富克斯羣研究二維曲面上的數學,瑟斯頓則用克萊因羣研究三維雙曲流形。在20世紀60-70年代阿爾福斯(Lars Ahlfors,1907-1996)、貝爾斯(Lipman Bers,1914-1993)、克拉(Irwin Kra,1937-)、馬斯基特(Bernard Maskit,1935-2024)和馬爾登(Albert Marden,1934-)等數學家工作的基礎上,他證明了雙極限定理、雙曲空間形變的緊性等,它們成為了證明瑟斯頓本人證明哈肯流形幾何化猜想和之後克萊因羣理論的重要工具。
正如龐加萊把微分方程、複分析、羣論、非歐幾何和曲面拓撲學貫通融合,瑟斯頓則將雙曲幾何、泰希米勒空間、克萊因羣和映射類羣、葉狀結構及其推廣、紐結論和三維流形理論等熔於一爐。見下圖:
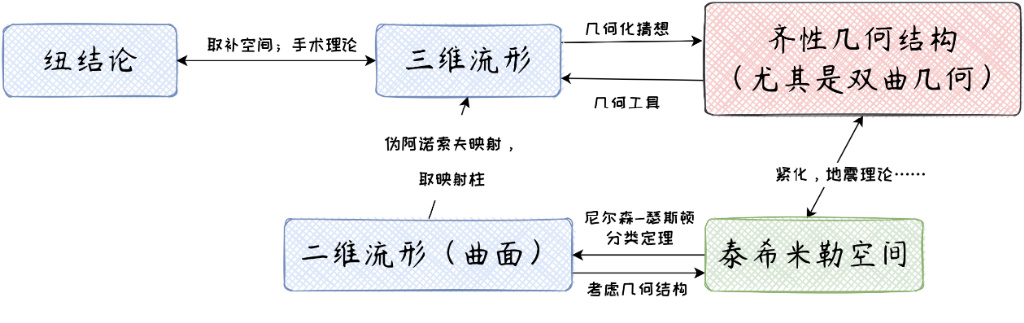
圖6
瑟斯頓的一系列經典文章和講義成為該領域研究者長期以來的必讀材料(如[24]),而他在研究過程中提出的問題也長期推動了低維拓撲學的發展。很有趣的是,與龐加萊類似,瑟斯頓並不太注重表述的形式化,所以他所發現的定理的很多完整證明都是後來由其他數學家所寫出的,而其中一些更復雜的證明很多也都使用了更高深的分析工具。
在幾何化猜想被證明後,低維拓撲領域的發展更加趨向豐富,與三維流形的雙曲幾何相關的重要猜想有馴順(tameness)猜想、庶幾纖維化猜想、庶幾哈肯猜想等等。其中,第一個猜想分別由Agol和Calegari-Gabai在2004年獨立證明;後兩個猜想則均由Agol在2012年證明。
由此可見,與科學與社會歷史領域的一切偉大變革一樣,龐加萊等數學家的獨創性工作的巨大意義和深遠影響,只有在更晚的時間才能更充分地看到,這正如魯迅所引用的叔本華的話:“要估定人的偉大,則精神上的大和體格上的大,那法則完全相反。後者距離愈遠即愈小,前者卻見得愈大。”
致謝:
本文感謝劉辛味編輯的支持鼓勵。在撰寫過程中,作者得到了北京大學北京國際數學研究中心劉毅教授、清華大學丘成桐數學科學中心林劍鋒副教授的大力幫助,特此致謝。
參考文獻
數學史:
[1] 克萊因, 19世紀數學發展史(第一卷)
[2] 莫里斯·克萊因, 古今數學思想(第三卷)
[3] 張生春,鄧明立, 十九世紀法國高等教育改革的啓示——兼談法國數學百年興衰
[4] 李文林, 數學的進化:東西方數學史比較研究, 科學出版社
單複變函數理論:
[5] 李培廉譯,黎曼文集,高等教育出版社
[6] F. Klein, Lectures on the Icosahedron and the Solution of Equations of the Fifth Degree
[7] Elias M. Stein, Rami Shakarchi, Complex Analysis(有中文譯本)
[8] Lars V. Ahlfors, Complex Analysis (有中文譯本)
龐加萊的原著及相關綜述:
[9] 龐加萊作品集, Oeuvres de Henri Poincaré
[10] J. Stillwell, Henri Poincare, Papers on Fuchsian functions
[11] Jeremy Gray, Henri Poincare: A Scientific Biography
[12] G. D. Birkhoff, The Work of Poincaré on Automorphic Functions
[13] Henri Poincare, Science and Method(中譯本:科學與方法,李醒民譯,商務印書館)
自守函數類:
[14] Joseph Lehner, Discontinuous groups and automorphic functions
[15] Lester R. Ford, Automorphic Functions
[16] 李國平, 自守函數與閔可夫斯基函數,科學出版社
模函數、數論與自守形式:
[17] Ranjan Roy, Elliptic and Modular Functions from Gauss to Dedekind to Hecke
[18] 馮克勤, 代數數論簡史, 湖南教育出版社
[19] 黑川信重, 栗原將人, 齋藤毅, 數論II: 巖澤理論和自守形式, 高等教育出版社
非歐幾何的起源與意義:
[20] 齊民友, 數學與文化, 大連理工大學出版社
多複變函數:
[21] 丘成桐、楊樂、季理真、馮克勤等編, 傳奇數學家華羅庚:紀念華羅庚誕辰100週年, 高等教育出版社
[22] 郭友中, 李國平院士對數學和數理科學的貢獻,數學理論與應用, 2011.1
富克斯羣,克萊因羣與三維流形:
[23] Alan F. Beardon, The Geometry of Discrete Groups
[24] William P. Thurston, The Geometry and Topology of Three-manifolds

特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權説明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。