什麼是最小二乘？_風聞

在統計分析和建模處理中，經常用到最小二乘的相關方法進行誤差分析處理。該方法的核心是所有估計值與被估計值之差的平方和達到最小。兩百年來，最小二乘思想的應用例子浩如繁星；到了最近十年，在新興的大數據科學以及人工智能疆場，到處都響着最小二乘的戰鼓。但會用相關的方法流程和計算工具，不一定就清楚背後的數學原理。釐清讀者朋友們“知其然而不知其所以然”的困惑，正是筆者寫作本文的一個初衷。

撰文 | 朱慧堅（玉林師範學院數學與統計學院副教授）、丁玖（美國南密西西比大學數學系教授）

我們發現，無論怎樣作一條直線，都不可能同時經過所有這五個點。見下圖：

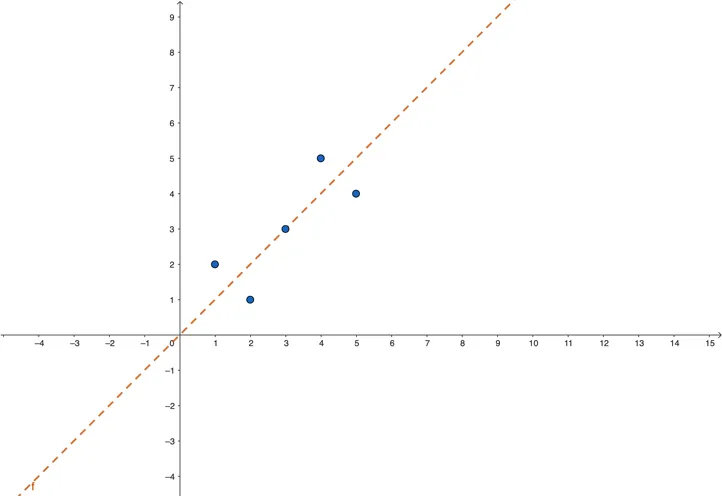讀者或許會説，兩個點決定一條直線，即給定平面上兩個不同的點，有且僅有一條直線經過它們。現在給了五個點，哪能有一根直線通過所有這些點？除非它們恰好位於一條直線上。你説對了，事實勝於雄辯。然而在現實世界裏，我們常常遇到這樣的問題：這些點是科學家或工程師為了尋求某種現象之客觀規律而獲得的實驗數據，數據依賴於測量，而測量就逃脱不了誤差。如果這個設想或期待的規律可表達為最簡單的線性函數（當然一般是複雜得多的函數，如攜帶了眾多參變量的有理函數、無理函數、三角函數、指數函數等，但本文旨在解釋思想，而非追逐細節），那麼這五組自變量和因變量的試驗值一般不可能都能精確滿足這個線性函數，從而產生了另一種誤差。

既然任何直線都不能由這些點精確表達，能否找到一根直線，使得它儘可能地“擬合”這些數據？自然，最佳的擬合就是插值，但這裏行不通，因為直線插值通常只能“插進”兩點，另三點只好落在線外。這樣，我們需要尋找另一種“最佳擬合方案”。這個最佳逼近所遵循的途徑就是本文主題“最小二乘”。

頭疼。對這類在某些點缺乏偏導數的多元函數，要得到其值為最小的最優點，不僅無一般解析公式可用，而且計算起來也很麻煩，因為基於微分概念的數值最優化方法（如最有名的牛頓法），這時沒有多少用武之地。

導數方法

上述二元函數的非光滑性來源於高中生都知道的事實：絕對值函數y=|x|在x=0時導數不存在。這個函數的圖像是直角座標平面第一和第二象限的對角射線之並，形狀像“身寬體胖”的大寫英文字母“V”，座標原點是它的一個尖點，在那裏曲線（折線）沒有切線。

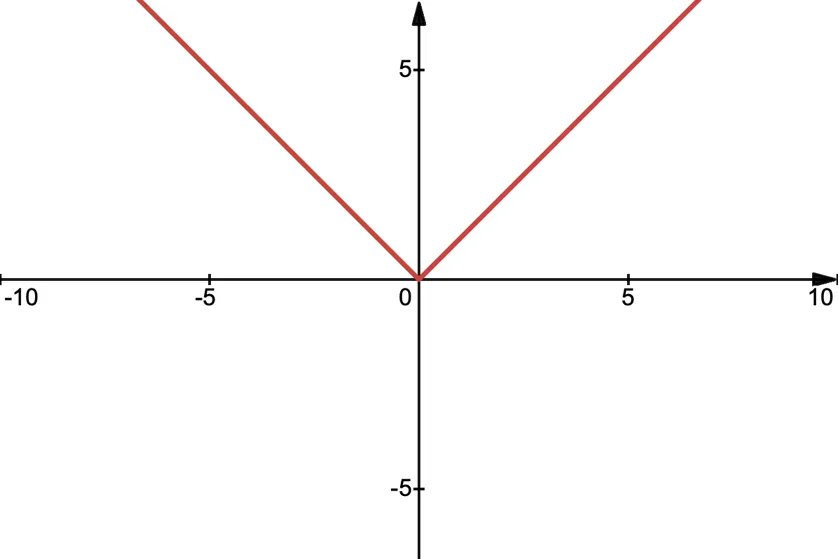y=|x|的圖像

那麼，怎麼解決上述不可微誤差函數最小值難以計算的困難呢？解決方案其實相當簡單，

範數在線性代數中極為有用，享有與長度一模一樣的幾個基本性質：

(i)範數總是非負數；

(ii)範數為0當且僅當向量為0；

(iii)標量與向量之積的範數等於標量絕對值乘以向量的範數；

(iv)兩向量之和的範數不大於各向量範數之和，稱為三角形不等式。

在泛函分析中，這四個性質成了在抽象線性空間上定義範數使其成為賦範線性空間的範數公理。

“內積”是歐幾里得空間裏十分重要的二元向量運算，結果為數，與幾何術語“正交投影”關係

矩陣方法

剛才求出最佳逼近用的是“導數法”，學過初等微積分的人都能理解，然而引進最小二乘的最常見手段卻是藉助於矩陣，和線性方程組有不解之緣，學過矩陣初等理論的讀者應該不會

但如果不像之前對五點線性擬合那樣耍弄微積分大刀，怎樣用線性代數的戰斧劈開它呢？現在我們搬出這把戰斧，它的木柄上刻着“正交投影”四個大字。

筆者在課上講解正交投影時，常用自己的身體做道具：微微向前傾斜身體，和地面成約80度的角（當然不能過度傾斜，否則會有倒地的危險），然後眼光垂直射向地面，從腳到眼光射到地面處的向量就是身體向量對着地面的正交投影。正交投影的一個基本性質是眾所周知的，即向量被正交投影后長度不能變大，用平面幾何的語言説就是：直角三角形的直角邊總不會比斜邊更長。斜投影沒有正交投影用途廣，就是因為它缺乏這個好特色。這也説明為啥人們都用直角座標系而幾乎不用斜角座標系，因為後者的兩點距離公式只能靠複雜的餘弦定律，而簡單漂亮的勾股定理愛莫能助！

在可見的二維和三維空間，正交投影與兩條直線段垂直幾乎就是同義詞。在解析幾何中，兩個非零向量相互垂直當且僅當它們的點積為零。到了線性代數里的高維歐幾里得空間，

基於對日常距離概念的直觀理解，我們可以把min{||x-v||: v∈V}稱為x到V的歐幾里得距離，簡稱距離。人人熟知，在連接直線外一點與直線上各點的線段中，垂線段最短。而上述引理將這個平面幾何的基本事實推廣到了高維歐幾里得空間，這將直接用於求解我們的最小二乘問題(3)。

歷史上，先是美國數學家穆爾（Eliakim Hastings Moore，1862-1932）於1920年定義了它，1955年，英國小夥子、2020年的諾貝爾物理學獎得主彭羅斯（Roger Penrose，1931-）又獨立地發明了它。

其次，這裏使用多項式函數進行最小二乘的問題，引出的A是個特殊矩陣。由於假設了這m

這實在是個簡潔漂亮的解公式！之前在《從線性算子的角度看廣義逆矩陣》中引進的穆爾-彭羅斯廣義逆在最小二乘誤差分析中大放異彩！自然，本文對五點問題用到的求導法，對此更一般情形也能得到同樣的結果，我們就暫時離開代數學，再次品嚐一下分析學的滋味。

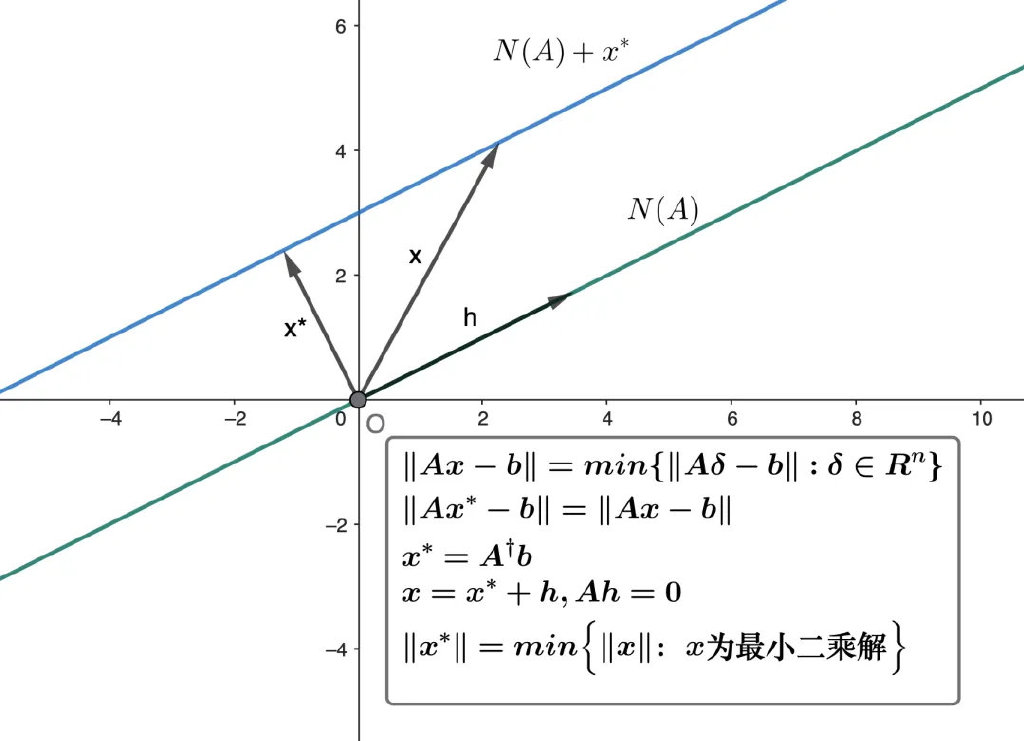
最小二乘問題和極小範數解

下面的圖示展現了極小範數最小二乘解的幾何意義：