熱力學平衡態對應的是最概然分佈還是所有分佈？_風聞

返朴-返朴官方账号-关注返朴（ID：fanpu2019）,阅读更多！1小时前

2025-05-27

熱力學平衡態中所有的微觀狀態都要出現，而非最概然分佈中的那些微觀狀態。如果試圖確定多能級系統中某單個能級上的粒子數，可以發現這個數會出現漲落，因此首先需要研究每個能級上粒子數的平均數。這個平均分佈具有基礎性意義，在一定條件下它和最概然分佈給出的分佈函數相等。統計物理證明通過這個平均分佈可以獲得熱力學量。

撰文 | 劉全慧（湖南大學）

一

王竹谿先生關於熱力學平衡態定義兩個似乎自相矛盾的評述

把一個盒子分成體積相等的兩半，盒子中充滿了大量的粒子且假設粒子可以分辨。平衡態時粒子只可能均勻分佈在空間內，或者説任意體積中的粒子的密度相等，兩個相等體積中的粒子的個數當然也相等。通過計算很容易驗證，均勻分佈是最概然分佈，包含的微觀狀態數最多。因此，王竹谿先生寫道：“最概然分佈相當於平衡態”。[1] 但是，王竹谿先生又告誡説，“最概然分佈相當於平衡態”很容易引起誤解，“即認為在平衡態時，只有對應於最概然分佈的微觀運動狀態才是可能實現的，這是錯誤的。在平衡態時，各種分佈都是可能的……”[1]

如果最概然分佈是一個分佈，肯定不可能包含所有的微觀狀態；如果平衡態包含了所有微觀狀態，則最概然分佈就不能對應平衡態。因此，王竹谿先生關於熱力學平衡態定義的兩個評述似乎自相矛盾。問題的答案不難，以至於任何一本統計物理的教科書中都沒有認真辨析這個問題；問題的答案並不顯然，我們最近佈置給學生一道思考題就是這個問題的具體體現，學生普遍覺得較難，説明這個問題遺留至今。

首先給出問題的答案。從數學的角度，最概然分佈特指一個或者極少數幾個分佈，就是上面的均勻分佈；但是在統計物理中，最概然分佈非指一個分佈，是全部分佈的平均，這個平均分佈包含了所有的微觀狀態數，不僅僅如此，這個平均分佈還必須是分佈函數。平均分佈的分佈函數才是統計物理等概率原理所規定的基本分佈。

二

一道《熱力學統計物理》思考題

玻色系統的微觀狀態數Ω，當簡併度=1的時候，每種分佈的微觀狀態數都是1，即Ω=1，參考圖1中的玻色系統的微觀狀態的個數的公式(6.7.2)，和圖2中一維諧振腔中的玻色氣體的分佈。這個時候，每種分佈的微觀狀態數都是1。因此這種情況下似乎不存在某一特定的分佈包含大量微觀狀態的情況，也就是沒有最概然分佈這種情況。問：如何理解通

圖2：一維諧振腔中玻色系統，粒子數和總能量的約束條件分別n=3， mℏω =3ℏω，圖中的0、1、2、3分別指第0、1、2、3能級。一共只有三種分佈，每種分佈的微觀狀態數都是1。為簡單起見，能量的零點為零，能量單位默認為ℏω。這個系統可以記為(m,n)=(3,3)。取自文獻[3]。

細心的學生都會自問這個問題或者對這個問題感興趣，參見附錄1。問題的答案就在高等統計物理教科書中，稍微超出了本科生課程的教學大綱。這是統計物理中的一個基礎性問題，通過簡單推理不難找到正確答案。但是，如果提給一位統計物理的教師或者研究者，他大概率也會有點懵。對於我們的學生來説，他覺得有些難度之後，自然會去尋找幫助，而現在他第一時間是求助於AI。聲稱是“綜合能力最強的AI——Gemini2.5pro”給出了答案。答案很長，説了很多正確的廢話，離正確答案相距甚遠，參見附錄2。

三

熱力學平衡態出現的是平均分佈而非最概然分佈

等概率原理是平衡態統計物理的基本原理。這一原理認為，對於孤立系統，平衡態中約束容許的所有微觀狀態都要出現且出現的概率是相同的，而不僅僅是最概然分佈中包含的微觀狀態。但存在微觀狀態特別多的最概然分佈時，有數學定理保證，當粒子數很大的時候，單一最概然分佈所包含的微觀狀態的個數的對數和系統全部微觀狀態的個數的對數近似相等。這個相等不是平衡態的核心，而是誤解的一個重要來源。如果不存在這一最概然分佈，如何定義平衡態呢？例如，一維諧振腔中玻色系統（參考圖2），每一種分佈都包含有相同或者近似相同的微觀狀態數的時候，必須考慮全部的分佈！這是等概率原理的直接表述，是獲得問題正確答案的出發點。

全部的分佈都出現就是每一個微觀狀態都出現，也就是各態歷經。

通過全部分佈中的微觀狀態，我們才能獲得統計物理中的分佈函數。分佈函數指的是，每個能級上粒子的平均個數和約束條件的關係。先不看統計物理中的分佈函數函數，只看數學上的平均分佈。以圖2中的系統為例，一共有三種分佈，也就是隻有三種微觀狀態。等概率原理認為，這三種微觀狀態出現的概率是相等的。全部微觀狀態中各能級上粒子的個數，即基態、第1、2、3個能級上的粒子的總數分別為3,4,1,1。由於系統中一共有3個粒子，四個能級上分佈粒子的平均粒子數分別是：

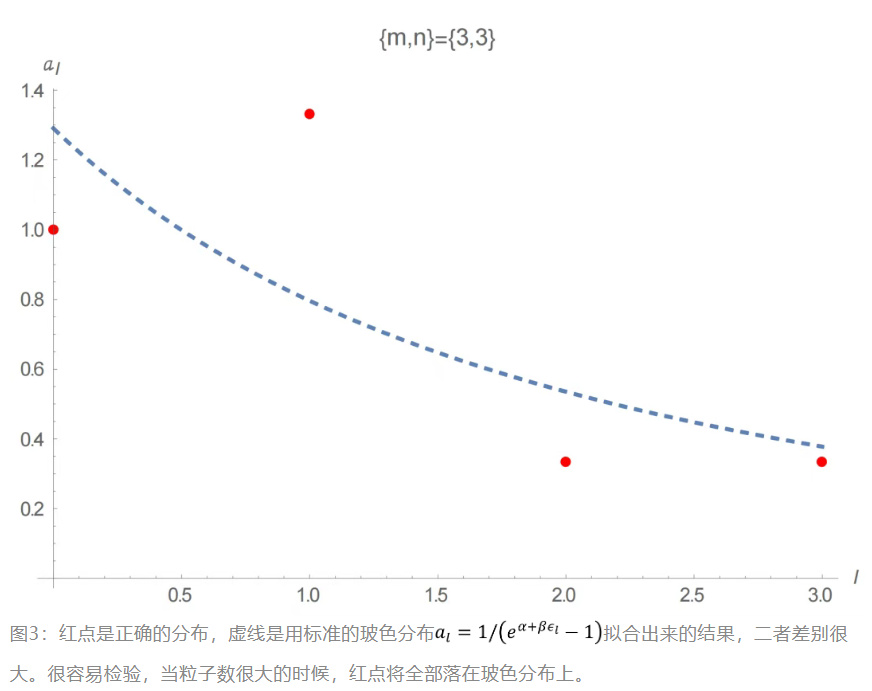四

平均分佈是統計物理基本分佈

下面考慮一般情況。對於任意一個系統，設分佈的個數是ℕ，基態上的粒子的總和是

可以把這個結果稱為Darwin-Fowler第二定理。(3)(4)兩式才是物理的分佈函數。

對於近獨立粒子系統，例如玻爾茲曼系統、玻色系統和費米系統，(3)直接給出標準的分佈結果。由於這個結果和通過最概然分佈給出的結果一樣，教科書常常把最概然分佈給出的結果認為是基本和普適的結果，這是一種誤解。從本文的分析可以看出，平均分佈是統計物理的基本分佈，最概然分佈給出的結果之所以有效，僅僅因為在一定條件下它碰巧和平均分佈相同而已。

上面分析中的ℕ即系綜中系統的個數，即圖2中的三種情況。一個熱力學系統將遍歷所有ℕ，即各態歷經。圖2中的系統清晰地解釋了為什麼最概然分佈會出現小數或者分數的情況。

五

結語

從等概率原理或者各態歷經假設可以看出，熱力學平衡態出現的是平均分佈而非最概然分佈，最概然分佈之所以正確是一種巧合，一種偶然。完全可以從平均分佈出發推導出玻色分佈的標準結果。

最概然分佈對應於平衡態，當且僅當最概然分佈是所有分佈的平均，即平均分佈。這是一種常見的情況，但不是全部，例外並不罕見，例如一維諧振腔中的玻色氣體。如果系統中所有的分佈包含的微觀狀態一樣多，我們必須直接處理所有的分佈；如果系統中有一部分分佈包含的幾乎全部的微觀狀態，則必須把這一部分的分佈全部考慮進來。

把Darwin-Fowler定理分離出來第一、二定理是合適的。第一定理説明平均分佈的原理性，第二定理説明最概然分佈等於平均分佈的巧合性。有專家輕視Darwin-Fowler理論，例如偉大的Mandelbrot就説過: “I have no love for Darwin-Fowler, …”[4][我不喜歡Darwin-Fowler（的理論）]。但是，這遮掩不了Darwin-Fowler理論的光輝。

最後，説明一下我們有一個普適的推導近獨立粒子系統分佈函數的新方法，即2022年關於少粒子系統的分佈函數的結果[6]。利用我發明的異步有限差分方法，不需要簡併度≫ 1的假設，可以證明標準的近獨立粒子的分佈函數適用於任意粒子數的系統。當系統粒子數很多的時候，當然也不需要 ≫ 1 的假設。不過我處理的系統，必須和庫相接觸，也就是和的數值必須由庫來決定，而不適用於處理孤立的少粒子系統。當粒子數很大，系綜的等價性開始發揮作用，我的結果也可以適用於處理孤立系統了。

致謝：感謝北京大學林宗涵先生、湖南大學張世豪教授、東南大學侯吉旋教授的有益討論。本項目受到湖南省重點教改基金（No. HNJG-2023-0147）資助項目。

參考文獻

[1] 王竹谿，統計物理導論[M],（北京：高等教育出版社，1956）p. 74. (引用原文時，“最可幾分布”被替換了現在的規範名詞“最概然分佈”。)

[2] 汪志誠，熱力學統計物理[M]，第四版，(北京：高等教育出版社，2008) p.185.

[3] 侯吉旋，最概然分佈的少粒子修正是必要的嗎?[J] 大學物理，41(12) (2022)p.1.

[4] Huang Keson, Statistical Mechanics [M], 2nd Ed. (New York: John Wiley, 1987)p.193.

[5] Mandelbrot B. B. Mandelbrot Replies [J], Physics Today, 42(3)(1989)p.156.

[6] Liu Q. H., Asynchronous finite differences in most probable distribution with finite numbers of particles [J], Ann. Phys. 441 (2022) p.168884.

附錄1. 優秀學生對思考題的第一反應，説明學生對這個問題也很有興趣。

學生對這個問題和答案的興趣。從學生的態度可以看出來，我在學生面前基本上沒有多少師道尊嚴。