走進“熵”的心臟：系綜——吉布斯理論追溯_風聞

學習統計力學時，系綜理論堪稱“攔路虎”，抽象概念常讓人困惑不已。為何孤立系對應微系綜？温度定義又為何引發爭議？本文追隨物理學家吉布斯的思想脈絡，從簡單的單擺模型入手，介紹如何應用劉維爾定理得到系綜理論，並討論時間平均、統計分佈與系綜分佈之間的關係，以期讀者可以從源頭瞭解吉布斯系綜理論。

撰文 | 徐曉（華南理工大學物理與光電學院）

從科學理論、文學作品到生活哲理，人們都特別喜歡引用“熵”的概念。

劉慈欣在《三體》中如此描述“歌者”：“宇宙的熵在升高，有序度在降低，像平衡鵬那無邊無際的黑翅膀，向存在的一切壓下來，壓下來。可是低熵體不一樣，低熵體的熵還在降低，有序度還在上升，像漆黑海面升起的磷火，這就是意義，最高層的意義，比樂趣的意義層次要高。要維持這種意義，低熵體就必須存在和延續。”“低熵”也成為了一個網絡上的熱門詞彙，因為“低熵”表示足夠有次序，不那麼糊塗，不那麼不確定。而這一比喻的來歷則和一個廣泛傳播的説法有關：熵即混亂度。

“熵”的最早思想來自熱力學，與混亂無關。把“混亂”概念和熵聯繫起來的，是統計力學這門學科。在統計力學中，乃至在應用數學理論、信息理論中，抽象而系統地講述“熵”這一概念，都離不開系綜理論。

可以説系綜理論是熵這一概念的“心臟”：通過它，熵的思想被泵到了各個不同的學科中。

系綜理論是抽象而艱難的學問。即使對於學習物理的學生，當學到系綜理論的時候，大多數人都難免犯迷糊。我有的同事，雖然教書也有年頭了，也坦言：不理解系綜。兩個典型的問題是：

在孤立系中，分出一個粒子數固定的小的系統，做正則系綜；再讓這個小的系統的粒子數不固定，做巨正則系綜。那從系統大小分，明明孤立系是整個理論的分析基礎，難道不應該是總系綜、小系綜、巨系綜嗎？為什麼系綜理論裏面，孤立系對應微系綜，然後才是正則系綜，巨系綜？

一種流傳較廣的説法是：孤立系不能定義温度。一個能量恆定且與外界不交換能量的系統，其中的粒子也有平均的動能，分明可以定義温度。這不是相互矛盾的講法嗎？

這些問題，不只在我讀書的時候犯迷糊，甚至我教授了二十年的《通信原理》，每年都要講一遍系綜平均和時間平均的關係的情況下，依然犯迷糊——畢竟像温度這樣的物理量，是物理學特有的，通信原理不會涉及。

最近，我由於寫書的緣故，讀了麥克斯韋（J. C. Maxwell）、玻爾茲曼（L. Boltzmann）和吉布斯（J. W. Gibbs）的書，豁然開朗，總算明白了“系綜”的來龍去脈。著名理論物理學家吳詠時先生認為，這始料未及而又豁然開朗的過程，是科學研究的趣味所在，不論心境還是內容都值得一書。

故有此文。

1

系綜理論提出的背景

為了從分子運動的角度解釋氣體的温度、壓強等物理量的成因，在克勞修斯（R. Clausius）的工作基礎上，麥克斯韋於1860年建立了氣體分子運動論。他將一個個氣體分子看作一個個彈性小球，從概率的角度引入速率分佈的假設，建立了描述氣體分子速率分佈變化的方程。而一個由大量氣體分子構成的體系進入統計平衡的狀態時（即宏觀的熱力學平衡態），氣體分子的速率分佈不再隨時間變化。[1]在OXYZ座標系內，這個穩定的分佈（速度分量）為

為了求H函數取極小值時對應的概率分佈密度，玻爾茲曼引入了一個假設：在總能量不變的前提下，體系中間各粒子處於不同速率的狀態的可能性是相同的。這個假設後來被稱為等概率假説。由此玻爾茲曼證明，當粒子數足夠多時，分子運動滿足麥克斯韋的速率分佈。而這個時候系統達至穩態，H取最小值。這樣，玻爾茲曼就證明了該分佈的唯一性。

然而，這些理論是把氣體分子當作彈性小球去處理的。所以有兩個問題，一個是忽略了分子間的相互作用力；另一個是忽略了分子的內部結構。

對於第一個問題，玻爾茲曼引入了分子間相互作用的力，即範德瓦爾斯力，修正了模型。而對於第二個問題，處理起來非常困難。在玻爾茲曼看來，當時的實驗僅僅是能觀察氣體發光的光譜，分子內部結構的解釋主要來自化學家，其力學結構是不清楚的。所以，玻爾茲曼只能採用相對抽象的力學理論，把一個分子看成一個力學體系，以分析力學為基礎，來建立分子內部結構的模型。正是這種分析辦法，使得玻爾茲曼不得不使用一個重要的概念——各態遍歷（ergodicity），來為其結果的合理性提供支撐，這也是吉布斯的系綜理論建立的起點。

現在我們結合玻爾茲曼的思路，來看看吉布斯的系綜理論。為什麼要結合玻爾茲曼的思路？據説，當年瑞利（John William Strutt, Third Baron Rayleigh）寫信給吉布斯，請求他寫一篇更長的文章來解釋其創立的相理論。吉布斯則答覆，認為原來的文章還太長，應該更短些。[4]所以，吉布斯的文章是出了名的抽象晦澀，充滿了看似倒因為果的推導和分析。因此，我下面就按照玻爾茲曼的思想脈絡，結合具體的力學體系的例子，來介紹吉布斯的系綜理論，以便讀者理解。

2

劉維爾定理

2.1 分析力學中的基本概念

對於一個力學體系，我們通常採用分析力學來進行處理，分析每個時刻體系的狀態。

對於系統勢能只與系統內物體的位置有關的力學系統，我們稱之為保守系統[5]，有：

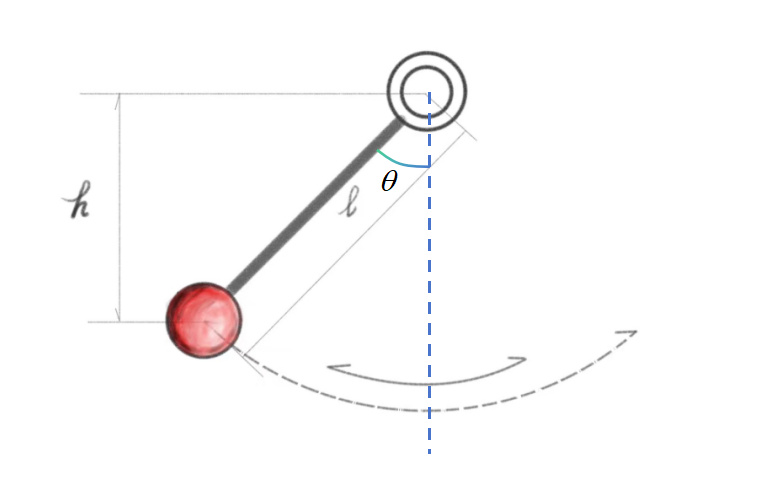圖1 單擺示意

容易看出，這個例子中，位形空間和動量空間的維度都是1，而相空間的維度為2。（見圖2）

如果體系受到除了位形決定的力的影響外，還受到其他力的影響，我們稱之為非保守系統。比如單擺的例子中，如果單擺運動到某個位置時，有人突然用手推了一下襬錘，或者擺錘被某個外來的小球撞了一下，系統就不再保守了。這個時候正則方程就會發生變化，寫為：

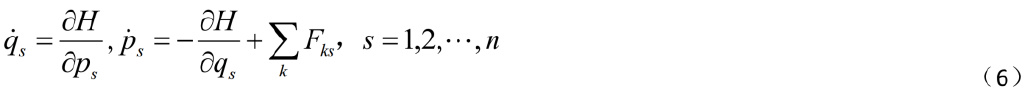
方程（6）似乎只是關於非保守系統的。但即使是保守力，如果被討論的施力物體在系統之外，並且處於運動狀況，則不把系統外部物體的動能以及其彼此間的勢能包含進系統，是無法消除Fks的作用的。玻爾茲曼和吉布斯都注意到了這一問題[6, 7]。本文後面討論略有涉及。由於問題複雜，筆者將另文探討。

2.2 各態遍歷

我們往往通過分析一個系統的參數在時間上的平均結果來刻畫系統。

比如，在前面所用的單擺中，我們要求系統的平均動能或者勢能，只要給定時間長度，對動能或者勢能按時間求平均即可。雖然這個時間平均結果會隨着起始觀察時間的不同而不同，但是隻要觀察時間足夠長，這些不同的結果將趨向一個定值，為系統總能量的一半。

這個問題也可以換一種方式來解決。

布。所謂求平均的過程，就可看作是一個求統計平均的過程。這個時候，“照片平均”和“時間平均”，不過是一種同義反復，沒什麼特別用處。

考慮一個盒子內的一羣氣體分子，我們將其中一個分子選作一個系統。在同一個時刻，各個分子雖然處於不同的運動狀態，但是其狀態彷彿處在某個分子某個時刻的狀態“照片”上。如果對整個盒子照張“全家福”，這張全家福就相當於某個分子各個時刻的照片PS到一起的結果。因此，只要照完全家福，然後針對全家福上的每個成員求統計平均，得到的結果自然就是時間平均的結果了。我們既可以用這個統計平均來代替時間平均，也可以用時間平均來代替這個統計平均。

但是，這裏有兩個潛在的問題：（1）這張全家福的成員狀態是不是平均地反映了某個成員各個時間段的狀況？會不會有的時間段的反映狀態比較密集，而有的時間段比較稀疏？（2）如果各個成員自然勾肩搭背，顯然和一個成員表演情況不同，則某個成員各個時間的照片PS起來，必定少了勾肩搭背的狀態。

抽象總結，選用一個成員各個時期照片也好，從整體的照片中抽取單個成員照片也好，都是要形成一個關於成員的“照片”的集合，同時選定了照片針對某個狀態的密度分佈。這樣選定的集合就是“系綜”。系綜（ensemble）的原意是指一個樂隊——儘管他們吹奏同一部作品，但是聲部、角色和吹奏強度則完全不同。

選定一個系綜以後，我們馬上面臨的問題就是：“時間平均”是否等於“系綜平均”？如果這個系統的運動隨着時間推移，系統按照一個系綜的分佈對應的概率密度，遍歷了系統可以處於各種狀態，我們則説系統是各態遍歷的。這時，時間平均自然等於系綜平均，二者的平均結果可以彼此替代。而研究這種替代性，正是玻爾茲曼涉及這一概念的初衷。

容易理解，對於一個複雜的系統，想象這些“照片”的情況都是複雜的事情，我們希望對這些照片情況的理解有更簡潔的方式。

2.3 吉布斯的“劉維爾定理”

現在我們來看，吉布斯是如何通過劉維爾定理來找照片的簡潔處理方式。需要順便解釋的是，劉維爾（P. J. Liouville）和吉布斯是兩個人，為什麼這裏叫吉布斯的劉維爾定理？劉維爾曾經在1783年處理了一個微分方程解的問題[8]，後來玻爾茲曼在處理分子體系的問題時，引用了劉維爾解方程的相關思想，所以玻爾茲曼將之稱為劉維爾定理[9]，而吉布斯則沿用了玻爾茲曼的叫法。但吉布斯的劉維爾定理，其內涵已經完全是統計力學的了。

現在回到我們的問題。針對單擺，如果我們不停地讓外來小球撞擊擺錘，則動能和勢能平均值既有可能隨起始觀察時間不同而不同，也有可能不會隨時間延長趨於一個定值。

現在我們限制條件，考慮在有外來小球撞擊情況下，時間平均在時間趨於無窮時趨於定值的情況。看看在這種情況下，有沒有辦法使用系綜平均。

外來小球的撞擊，每一次都改變了系統的能量。因此，容易想象，按照一個合理的分佈，既選取系統能量不同的單擺的照片，也選取同能量的單擺運動處於不同時間的照片，應該可以使用系綜平均的結果。

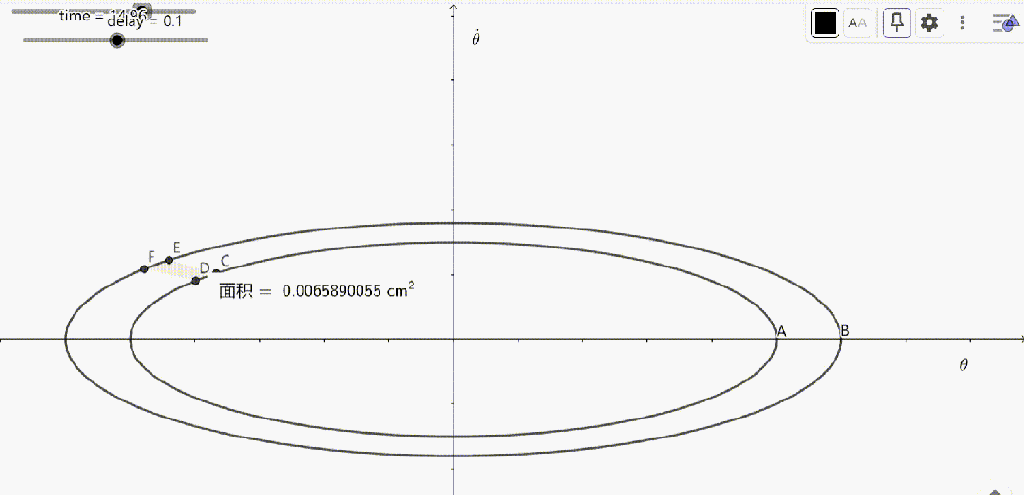圖3. 劉維爾定理：相體積不變

吉布斯採用一段非常數學化的語言，來描述劉維爾定理：“當相空間中的限定於一定相空間範圍的相按照系統（內外）的力——這些力是位置座標的函數，同時函數可以顯含或者不顯含時間，所遵循的動力學規律隨時間變化時，其限定的範圍的體積值保持恆定。”（吉布斯的原文為：When the phases bounding an extension-in-phase vary in the course of time according to the dynamical laws of a system subject to forces which are functions of coordinates either alone or with the time, the value of the extension-in-phase thus bounded remains constant.）[11]

即由公式（7）和（9），有：

公式（10）即劉維爾定理的數學表述。

在劉維爾定理的基礎上，我們容易得到以下結論：對於一個保守系統，比如單擺的振幅不

不會隨時間變化，達到穩定狀態，則時間平均和系綜平均結果相同，各態遍歷。需要注意，這裏是ρ對t的偏微分，這和全微分的含義是不一樣的。全微分時，系統的廣義座標和廣義動量都會隨時間而變，但偏微分時它們不會隨時間而變。

如果單擺不斷受到外來撞擊，我們可以認為系統從一個能量範圍的保守系統系綜跳到了另一個能量範圍的保守系統的系綜。那麼，如果針對某個能量值選擇的相空間所有微元的概

合理而穩定地選擇外來作用，使系統可以進入統計穩定狀態，且各態遍歷。

3

系綜理論

3.1 正則系綜

對於一個熱力學系統，我們也是通過一定時間的觀察，來獲得相關的熱力學量的。也就是説，我們通過時間平均來求取參數。比如一個容器內有1摩爾氫氣，我們是可以通過一定時間觀察温度計而得到温度，觀察壓力傳感器而得到的壓強的。但是，從微觀角度分析這個過程，我們必須考慮6.02×10^23個氫氣分子中，每個分子的三個平動和三個轉動座標，考慮相互撞擊以及彼此間的範德瓦爾斯力，還要考慮分子內部兩個氫原子之間的振動和轉動，要考慮分子受到容器壁撞擊而致體系內外能量發生傳遞，就像單擺擺錘受到撞擊一樣……

顯然，我們可以像前面處理單擺一樣，來分析容器內的1摩爾氣體。當然，現在系統的自由度要大得多，有6.02×10^23×（6+2）個自由度。但是，對於這樣的正則系統的系綜，應該使用的分佈，是什麼樣子呢？

如劉維爾定理一節所述，只要對相同能量的狀態賦予等概率值，針對概率能量差異而得的分佈，可以是任何形式。而吉布斯則沿着麥克斯韋和玻爾茲曼的路子，選用了麥克斯韋-玻爾茲曼分佈。這種選擇背後，自然是正態分佈。這是吉布斯的正則系綜理論暗含的一個前提。雖然，從表面上看，吉布斯似乎“證明”了一定要選擇這個分佈。吉布斯選用的分佈，按

這個分佈對應了一個名字，就是正則分佈。這實際上就是玻爾茲曼分佈的一個推廣。

雖然吉布斯經過長篇細緻的推導，來説明這一選擇的合理性，但在關鍵處，他依然指温度與熵和概率因子的對應性，這是通過與玻爾茲曼等人的結果“對比”而得來的。換言之，這種選擇，並不是從劉維爾定理出發，經過嚴密推導而得的結果，而是吉布斯主動預設的。

從力學系統分析出發，然後類比到熱力學系統，建立熵、温度和壓強等熱力學量與力學系統的物理量之間的對應性，在吉布斯建立系綜理論之前，就有相應的研究脈絡。赫姆霍茲（H. von Helmholtz）、玻爾茲曼和麥克斯韋等物理學家都做過類似的類比。而且歷史文獻表明，在1890-1900年吉布斯逐步建立理論的時期，他對這些工作是相當熟悉的。12這一點，在一般的教科書裏幾乎很難找到説明。[13]如果不熟悉歷史，自然會對吉布斯使用這一類比感到抽象和奇怪，就會難以自然理解整個系綜理論。

現在我們回到單擺的例子，來看看這種對應性。

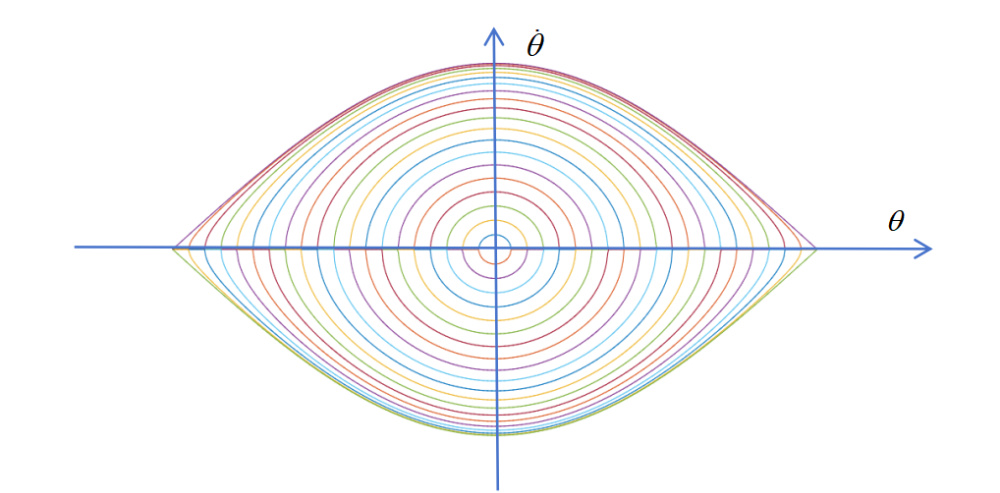
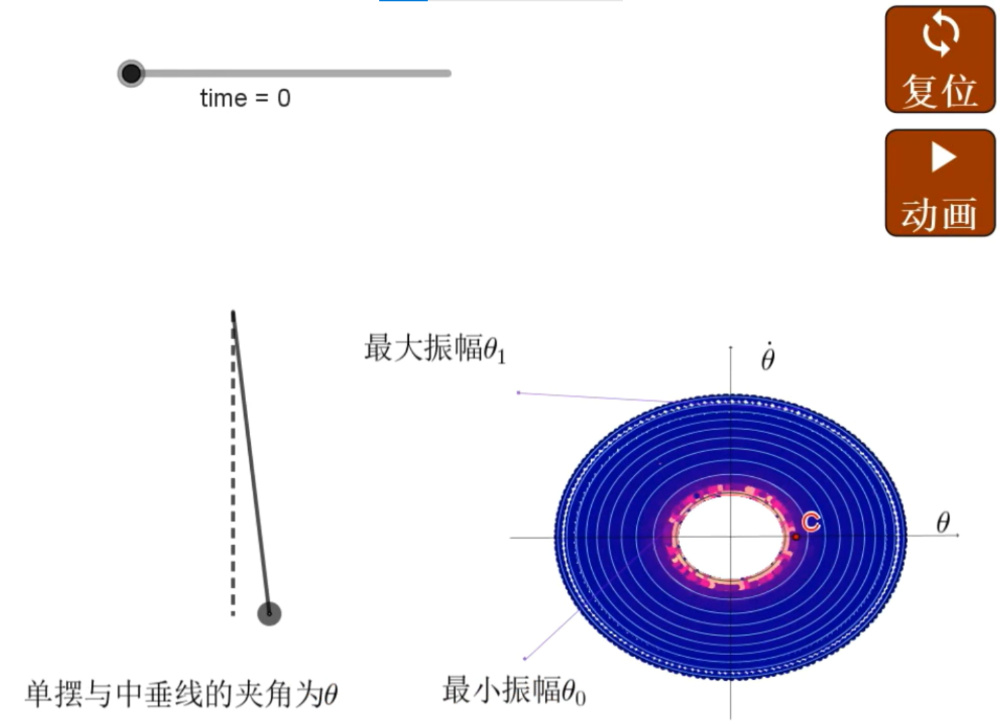圖5 單擺軌跡的最後分佈

在動畫中【前往“返樸”觀看】，單擺最大振幅一定，則能量一定，擺球沿着等能線運動；當受到外來擾動時，單擺改變振幅，即從一個等能線調到另一個等能線運動。系統的擾動類似公式（13），是按照概率隨能量指數變化而設定的，能量越高，單擺到達的可能性越小；最後單擺的軌跡分佈則表明了能量軌道按指數分佈的情況。軌跡圖中，顏色越偏粉紅，概率越大；越偏藍，概率越小（如圖5）。容易想象，按照這張軌跡圖，我們可以相應定出單擺系統的統計“温度”。

3.2 微正則系綜

微正則系綜是一個特殊狀況。

微正則系綜選擇的系統都具有同樣的能量。由於劉維爾定理的要求，微正則系綜對相空間的狀態選擇了等概率分佈。從集合的角度看，一個典型的正則系綜，是由一系列微正則系綜“粘合”而成，所以微正則系綜是正則系綜的子集。這也正是“微”這個詞的由來。從前面單擺的例子中，我們也可以看出這一點。

在統計力學發展之初，温度被理解為一個系統中每個粒子在三維空間中的某個方向的平均動能，後來經過玻爾茲曼處理，温度被理解為一個力學體系（這個力學體系當然是為了描述微觀粒子的運動的）各個獨立自由度對應的平均動能。因此，一個微正則系綜是可以定義温度的。

仍以單擺為例。顯然一個單擺構成的系統，只有一個自由度，其温度即為其平均動能，即

需要強調的是，這裏單擺是一個玩具式的模型，是關於微觀粒子運動的一個抽象或“類比”，而不是真的有個單擺系統有“温度”。但是，以上內容也提示我們，所謂温度，有兩個不同的定義：一個是系統平均動能，這是物理學科的通常理解；另一個是關於熱力學系統的統計參量，是統計力學所特有的。

3.3 巨正則系綜

巨正則系綜，按照吉布斯的定義，則是由自由度不同的系統構成的系綜進一步合併而形成的系綜。比如，有一個空間區域，有N個氣體分子，這個空間區域和N個氣體分子構成的系統的各種可能狀態及其分佈，就構成了一個系綜。如果我們選用正則分佈，那麼這個系綜就是正則系綜。以同樣的方式，在同樣的區域和相同的外部條件下，我們還可以得到一個有N+1個分子的正則系綜。我們把由N個，N+1個，……分子的系統構成的各個系綜合並在一起，就得到一個巨正則系綜。而由巨正則系綜得到的分佈，則與體系自由度的選擇緊密相關，在相空間中，這個分佈為：