1^ᵏ+2^ᵏ+ ⋯ + n^ᵏ = ?_風聞

這裏我們介紹一種基於分部積分法的處理方法，不僅能獲得連續自然數冪次的一般求和公式，還能附帶證明一個有趣的猜想。説不定讀完本文後，聰明的你也會靈感迸發，開闢一個與眾不同的新解法。

撰文 | 朱慧堅（玉林師範學院數學與統計學院副教授）、丁玖（美國南密西西比大學數學系教授）

讀者朋友看到本文標題，或許會不以為意地發笑一聲：這還不簡單，不就是

對，您説的大致不錯，如果再去查一查微積分教科書，或許還可以繼續看到公式

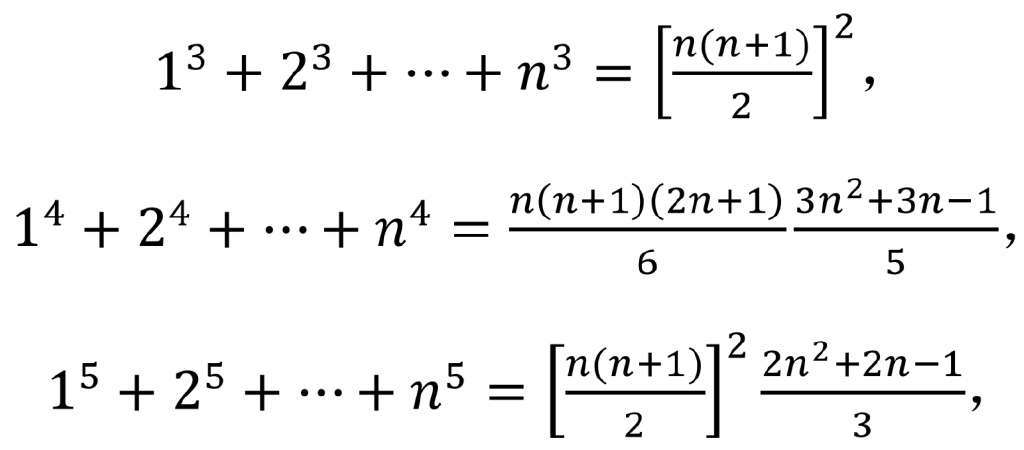等等，等等。但是，如果有人請教您1^100+2^100+⋯+n^100等於什麼，您能馬上告訴他相應的公式，或指導他如何下手嗎？更進一步地，在仔細察看了上面的六個代數恆等式後，您可能會突然發現，平方和表達式n(n+1)(2n+1)/6恰好是四次方和表達式的一個因子，立方和[n(n+1)]^2/4恰好是五次方和的一個因子。這時，您肯定在納悶這僅僅是巧合，還是説對六次和七次冪，甚至更高次冪的求和公式也都是如此。好吧，我們再瞧一瞧接下來的三個公式：

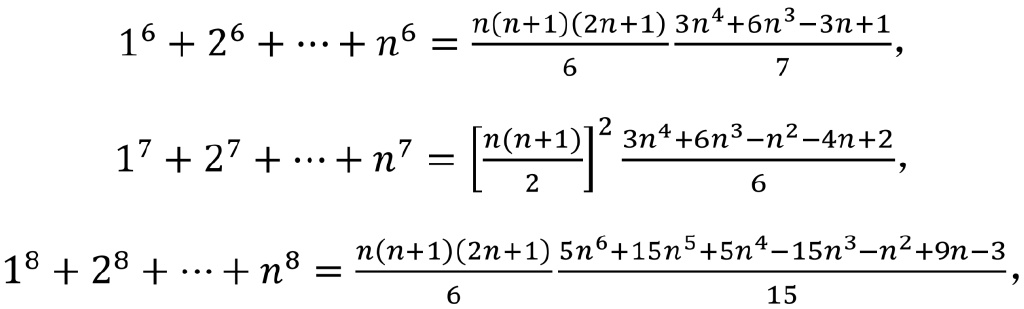結果發現同樣的模式依然存在。這似乎是個有意義的觀察，勾起我們的好奇心：對一般的正奇數k>1或正偶數k，從1到n的連續自然數k次冪之和的表達式是否分別具有上面所説的因子？

在全世界流傳百年之久的傳奇故事是這樣説的：高斯年幼時，他的老師為了整治班內淘氣學童，要求學生計算1+2+⋯+99+100。聰明的小高斯將其反方向寫成100+99+⋯+2+1，再與原式上下對齊，縱向相加，加出了100個同一個數，該數乘以100再除以2，便在片刻之間算出答案

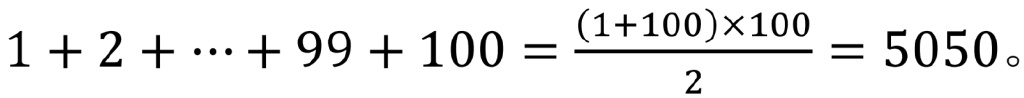這個數學傳奇激勵着天下俊傑對各種形式的自然數羣體相加、相乘尋覓規律，破解謎團。作為一個佳例，從古到今不知有多少人熱衷於發明新的方法，回答本文標題所提的數學問題。為了建立一個既封閉又悦眼的求和公式，所涉及到的數學工具實在是五彩繽紛，思路和技巧各種各樣，又“條條大道通羅馬”，顯示出不同數學分支之間的密切相關性。在這些手段中，有的是基於組合數學的生成函數概念，有的是運用線性差分方程的理論，也有的甚至借用了初等微分學裏的洛必達法則。幾何中最有名的勾股定理據説已有約五百種證明，但我們還不清楚現在有多少種辦法能夠導出自然數同冪次求和的表達式。説不定讀完本文後，有個聰明而好奇心極強的讀者會滋生靈感，磨礪出一把新斧頭，開闢一個與眾不同的解法。這裏，我們介紹一種基於分部積分法的處理方法，它歷史悠久，不僅能獲得連續自然數冪次的一般求和公式，而且還能證明上述關於和式因子結構的猜想為真。它來自於數值積分中一個著名求和公式對單項式函數的巧妙應用，曾被作者用於證明同事提出過的上述猜想，那時作者正為大學高年級學生和研究生開設一門數值分析課程，恰好在課堂上講授到那個積分近似公式。

歐拉-麥克勞林求和公式

初等微積分裏有關於不定積分和定積分的分部積分法，對於定積分，它指的是如下的等式：

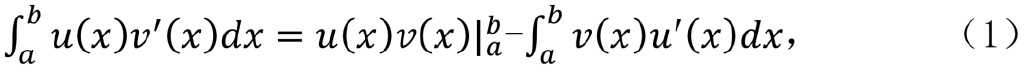
學過初等微積分的讀者都知道，不定積分的分部積分法就是函數導數的乘積法則

[u(x)v(x)]’=u’(x)v(x)+u(x)v’(x)

通過移項寫成等價形式u(x)v’(x)=[u(x)v(x)]’-u’(x)v(x)後，用不定積分的數學語言

∫u(x)v’(x)dx=u(x)v(x)-∫v(x)u’(x)dx

而重新表述的。這和將陳述句“老布什總統是小布什總統的父親”等價地寫成“小布什總統是老布什總統的兒子”是同一個道理。至於定積分的分部積分法（1），它就是將上述不定積分的分部積分法同微積分的最重要定理——微積分學基本定理

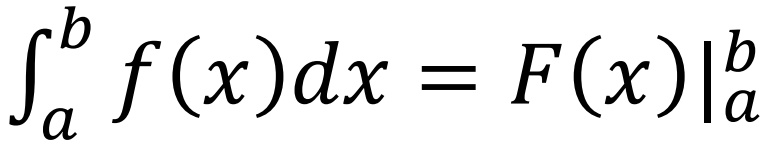F(x)是f(x)的一個原函數，即在區間[a, b]上恆有F’(x)=f(x)相結合後的自然產物。

在定積分的計算中，如果被積函數可以寫成乘積u(x)v’(x)的形式，並且上面（1）式右端的定積分值相較左端可以更容易地計算出來，那麼此時的分部積分法算是用對了，這是定積分計算技巧中的通常思路。比如，要計算出定積分

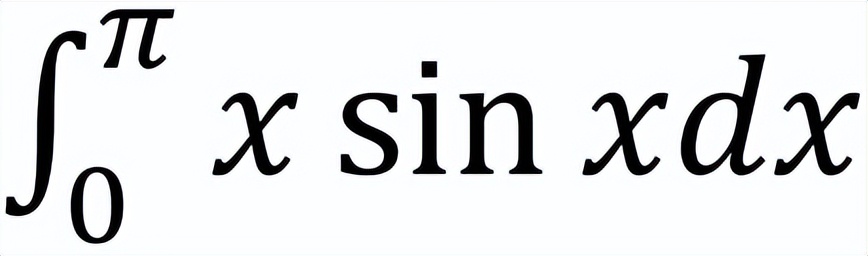如果令u(x)=x及v’(x)=sinx，則u’(x)=1，並且sinx的一個原函數是v(x)=-cosx。然後，（1）式給出

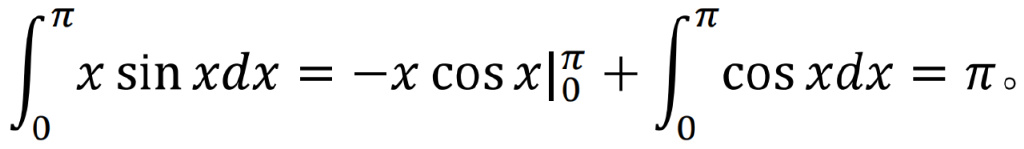
這就與計算初衷南轅北轍，因為等式右邊定積分中的被積函數看上去更加複雜，無法直接知道它的原函數是什麼。這充分説明，在運用分部積分法之前，一定要聰明地選對公式（1）左端中的這兩個因子函數u(x)和v’(x)。為了本文要講述的主題，我們先請讀者注意，在（1）式中，v(x)只需是v’(x)的一個原函數，因為根據微分學基本定理（即教科書裏通常所稱的拉格朗日中值定理），同一個連續函數的所有原函數之間只相差某個常數，因此該v(x)的選用有一個自由度，這給下面構造“歐拉-麥克勞林求和公式”提供了極大的方便。

現在，我們就“聰明地”選擇分部積分法中的u(x)和v’(x)，並反覆運用（1）式，建立一種逼近定積分的數值積分方法——歐拉-麥克勞林求和公式。設想f(x)是一個光滑函數，意思是它直到某一個所需階數的所有導函數在定義域上都是逐點連續的，其定義域為閉區間[0,

因為被積函數多了一個二次多項式的因子。然而，如果我們略微耐心一點，很快就會發現事實上這是一個聰明之舉。

性急的讀者或許從上式右端第二項的結構預測：它後面的積分可以繼續用分部積分法展

（3）是建立前n個自然數同冪次求和公式的一個理想工具。

歷史上，歐拉-麥克勞林求和公式於1732年由瑞士數學家歐拉（Leonhard Euler，1707-1783）發現，但未及時發表。1736年他與蘇格蘭數學家斯特林（James Sterling，1692-1770）通信時得知蘇格蘭數學家麥克勞林（Colin Maclaurin，1698-1746）對此獲得更一般的結果後，放棄了自己的優先權。兩人各自的公式分別發表於1738年和1742年。後人將此用途廣泛的等式以他們的名字命名。公式推導中引進的這一族多項式p1(x),p2(x), …被標準化後，與比他們更早半個世紀的瑞士數學家雅各布·伯努利（Jacob Bernoulli，1654-1705）發生了聯繫，而與後者名字也分不開的一列數字則對本文的主題貢獻良多。

瑞士巴塞爾的伯努利家族聲名顯赫，學者雲集，一門三代出了八位數學家。雅各布·伯努利是第一代中的“大哥”，他探索過的眾多數學對象包括無窮級數和一類後來冠以他姓的微分方程，概率論中的大數定律是他的一大傑作，而銀行家們最感興趣的連續複利問題由他解決，導致絕對常數e=2.7128⋯的出世（代表此數的通用字母e則來自於歐拉）。

雅各布·伯努利為自己設計的墓碑也藴含了數學巧思，他希望在墓碑上刻一條數學意義豐富的對數螺線，根據雅各布本人的解釋，這根自相似螺線“可以象徵逆境中的堅韌和恆心，也可以象徵人體在經歷所有變化甚至死後，也能恢復到精確完美的狀態。”可惜在他去世後，或許是雕刻墓碑的工匠誤解了指示，錯誤刻下了不相干的阿基米德螺線。

雅各布·伯努利的墓碑，螺線周圍的拉丁文Eadem mutata resurgo意為“縱使變化，依然故我”｜Wikipedia

雅各布的二弟約翰（Johann Bernoulli，1667-1748）微積分本領超越常人，常與大哥爭強好勝，如比賽求解“最速降線問題”，甚至也曾向牛頓叫板，結果是後者提速了變分學的發展。約翰不僅培養和提攜了少年歐拉，而且伯努利家族在他這一支湧現出的數學家最多。雅各布的大弟尼古拉斯是個畫家，其子尼古拉斯一世（Nicolaus I Bernoulli,1687-1759）在伯父的教導下成長為數學家，對微分方程等學科多有建樹。約翰的兒子丹尼爾（Daniel Bernoulli，1700-1782）對概率論有開創性研究，也是歐拉的同事和親密戰友。在伯努利家族中，上述幾位是我們在大學教科書中見過面的傑出代表。第三代中的數學家約翰三世（Johann III Bernoulli，1744-1807）則是個多才多藝的罕見神童。

伯努利多項式與伯努利數

顯見它們是正負交錯的。

現在我們用數學歸納法證明出伯努利多項式在標準的單項式基底下的一般表示形式。

引理1. n階伯努利多項式具有表達式