這位幻想藝術家的畫作中,藏着驚人的數學奧秘_風聞
返朴-返朴官方账号-科普中国子品牌,倡导“溯源守拙,问学求新”。15分钟前
在繪畫藝術作品中,不乏含有精妙的數學元素,比如完美的幾何圖形、分形、黃金分割等。當然,很多數學解讀是後來人們為之賦予的,創作者本身並不瞭解其中的奧秘,此時藝術與數學卻和諧交融。本文介紹的藝術家艾瑪·昆茨的作品正是這樣一個例子。饒有趣味的是,昆茨本人是一位通靈治療師,她沒有正規的藝術背景,從事的工作在如今會被貼上偽科學標籤。但她在幫助患者過程中創造了超越時代的藝術作品,得到了今天藝術界極高的評價。畫作中顯而易見的數學內容,不僅吸引了公眾的目光,也讓專業的數學家感興趣——他們發現,昆茨作品中有許多包絡線。
撰文 | Sumit Dhar、Pamela Gorkin Sofi Jeffrey(巴克內爾大學數學系)
翻譯 | 許釗箐
艾瑪·昆茨(Emma Kunz,1892-1963)是瑞士的研究者、幻想藝術家,也是一名心靈療愈師。為了幫助她的患者,她使用輻射感知療法(radiesthesia),一種涉及占卜擺錘的技術,她認為擺錘受到能量場引導。把使用擺錘所得到的點用石墨線連起來,再填上顏色,她創造出許多幾何圖畫。這些作品有時會被稱為精神(spiritual)藝術或者幻想(visionary)藝術,如今已多次在重要的個人展和羣展中展出。1993年,她的作品No.095(圖1)甚至登上了瑞士郵票。
儘管昆茨使用她的藝術來答疑解惑,並深入瞭解她的患者,但我們特別感興趣的是那些繪畫展現的數學內容。她創作的曲線可以被看作是眾多直線的包絡線,因此我們可以在包絡算法的幫助下進行分析。事實上,在我們所研究的作品中,昆茨反覆運用了一種技法,這使得那些出現在她諸多作品中的包絡曲線能夠被計算出來。而她對色彩、鏡像、平移和旋轉的巧妙運用,又使這些作品各具特色。本文將探討昆茨作品中的圖案、數學變換,以及能夠揭示其結構的原理。我們相信,這一研究為包絡算法提供了一個理想的應用實例。
 圖1 1993年發行的瑞士郵票,以昆茨的095號作品為圖案。
圖1 1993年發行的瑞士郵票,以昆茨的095號作品為圖案。
艾瑪·昆茨與她的作品
艾瑪·昆茨(圖2)1892年出生於瑞士阿爾高州一個貧窮的織工家庭。1909年對她而言尤為艱難:那一年,兩位姐妹去世,之後父親也自殺了。不久之後,她開始使用擺錘進行預言、心靈感應以及療愈。19歲時,她邁出了不尋常的一步——前往美國追求自己的興趣愛好。然而一年之後,她失望地回到了瑞士,並重新開始施行心靈治療。
 圖2 艾瑪·昆茨(圖片由艾瑪·昆茨基金會提供)
圖2 艾瑪·昆茨(圖片由艾瑪·昆茨基金會提供)
此後,昆茨在一家針織廠打工養活自己。1923年至1939年間的夏季,她在具象藝術家和藝術評論家雅各布·弗里德里希·菲爾蒂(Jakob Friedrich Welti,1871-1952)的家中擔任管家,並在此後與這一家族建立了深入的聯繫。在1942年,昆茨開始在毫米方格紙上作畫,並和她在布里特瑙的姐妹一起發現了一種“瑞士治療石粉”,名為AION A。1939年,她離開了菲爾蒂家族,並搬到了離她兄弟更近的地方,之後在阿彭策爾的瓦爾德施塔特附近建造了一所房子,因為這裏允許她實踐自然療法。
有關艾瑪·昆茨的生平和工作的信息收錄在她的一位患者安東·邁爾(Anton Meier)所著的《艾瑪·昆茨》(Emma Kunz)一書中[9]。他們第一次相見時,邁爾患有小兒麻痹症,他的父親帶他去拜訪昆茨。“第一次治療時,昆茨展現了(AION A)巨大的治療能力”(注1:參考https://www.emma-kunz.com/en/)。安東康復了,他們也成了朋友。
邁爾目睹了昆茨的工作過程:“直到今天,我都不敢相信她可以用擺錘那麼快地找到那些點並靈活地繪製線條。沒有數數,沒有計算,沒有測量,也沒有構造。”[9,P.30] 她對着擺錘發問,範圍從政治到個人或者哲學。她用擺錘軌跡提供的點,繪製線條並增添顏色。她的眾多作品都沒有標題,也不標記日期,她相信這樣可以讓它們以新的方式被詮釋。
儘管這個過程表面上沒用測量、計數和計算,但許多她在方格紙上創作的作品(甚至可能是大多數)都使用了等距線條、對稱或者幾何圖形。正如昆茨所説,“我的作品是為了21世紀而設計。它們傳達了作為維度、韻律、符號、數字和原理變換的構造和形式。”(注2:參考https://www.emma-kunz.com/en/)
艾瑪·昆茨於1963年1月16日在瓦爾德施塔特去世,後被安葬在布里特瑙。1986年,邁爾創立了艾瑪·昆茨中心(Emma Kunz Center)來保存昆茨的探索和創作。參觀者可以遊覽附近的洞室,艾瑪曾在那裏發現了AION A。
昆茨創作語境
2018-2019年,《世界接收者》(World Receivers)展覽會在慕尼黑舉辦。正如該展覽的策展人所言:
《世界接收者》展覽帶領觀者走入現代主義歷史中一段非凡而鮮為人知的篇章:英格蘭的喬治亞娜·霍頓 (Georgianna Houghton,1814-1884),瑞典的希爾瑪·阿芙·克林特(Hilma af Klint,1862-1944),以及瑞士的艾瑪·昆茨,她們各自完全獨立地發展出具有豐富含義的高度抽象視覺語言。她們都致力於在作品中將自然規律、精神世界與超自然現象加以可視化,並以堅定而自信的姿態追隨各自的信念。[1]
這並非孤例:人們常將艾瑪·昆茨與更廣為人知的希爾瑪·阿芙·克林特相提並論,但不同的是,阿芙·克林特受過專業藝術訓練,而昆茨並無正規藝術背景。她們兩人同屬於抽象藝術家的行列,只有個別作品的確具有一定的相似性(可對比圖3右側克林特的作品與左側的昆茨的作品)。
 圖3 左:昆茨第168號作品,現印於Aion A產品包裝上(圖片由艾瑪·昆茨基金會提供)。右:希爾瑪·阿夫·克林特作品, Altarpiece No. 1, Group X,1915年,布面油畫並使用金屬箔(圖片由希爾瑪·阿夫·克林特基金會提供)
圖3 左:昆茨第168號作品,現印於Aion A產品包裝上(圖片由艾瑪·昆茨基金會提供)。右:希爾瑪·阿夫·克林特作品, Altarpiece No. 1, Group X,1915年,布面油畫並使用金屬箔(圖片由希爾瑪·阿夫·克林特基金會提供)
具體而言,阿芙·克林特早期的作品呈現出鮮明的幾何風格;她也將通靈實踐融入創作,試圖通過降神會與超自然存在進行溝通。(注3:在那個時代,許多人自認為是通靈者,其中包括英國自然學家、進化論生物學家阿爾弗雷德·拉塞爾·華萊士(Alfred Russel Wallace, 1823-1913)。美國第一夫人瑪麗·託德·林肯(MaryToddLincoln,1818-1882)甚至曾在白宮中舉行通靈會。數據顯示,僅在19世紀後期,美國有400萬至1100萬人自稱是通靈者[3]。)
然而,由於阿芙·克林特將其主要作品私藏,並且要求在她去世20年內不得公開展示,所以昆茨等人幾乎不可能受到她的影響。直到1986年,阿芙·克林特的作品在洛杉磯郡藝術博物館的《藝術中的靈性:1890-1985年抽象繪畫》(The Spiritual in Art: Abstract Painting 1890–1985)展覽中作為具有爭議性展品之一展出,才開始獲得廣泛關注。此後,阿芙·克林特的作品接連亮相於多個國際重要展館,包括丹麥的路易斯安那現代藝術博物館和美國的古根海姆美術館。(注4:部分畫作的作者身份,至今仍存爭議[14]。)
昆茨的創作於1973年開始被認可為藝術作品,這比阿芙·克林特1986年的展覽早了13年。昆茨的作品曾在瑞士的阿爾高藝術館展出,併入選了哈拉德·塞曼(Harald Szeemann)1975年策劃的展覽《單身機器》(The Bachelor Machines)。(注5:塞曼是一位瑞士策展人、藝術史學者,一生策劃超過兩百場展覽,其中許多展被認為具有開創性意義。策展人過去主要是藝術品的看護者與展覽的執行者。但在整整50年前,塞曼在伯爾尼美術館策劃的一場劃時代的展覽,徹底打破了這一界限——他的影響幾乎可以説是無限大的。1961年塞曼就成為館長,那時他年僅28歲。[13])
塞曼特別指出,在1991年-1992年蘇黎世藝術館的《預見瑞士》(Visionary Switzerland)展覽、馬德里的索菲亞王后國家藝術中心博物館,以及杜塞爾多夫藝術館舉辦的展覽中,昆茨的作品均引發廣泛關注。2019年,昆茨四十餘幅罕見畫作[6]亮相倫敦蛇形畫廊,這次展覽被描述為“已故瑞士幻想藝術家、療愈師和研究者艾瑪·昆茨在英國的首次個人展覽”。該展與瑞士格勞賓登州的蘇施博物館共同策劃。蛇形畫廊官網援引了塞曼的評價:
(昆茨的)天賦在於她能夠感知那些既違背日常經驗、又超越自然科學與藝術法則的隱秘聯繫。這是一種超自然現象,一種奇蹟——在揭示神聖真理的同時,傳遞着一種與宇宙創生同頻的隱秘脈動。艾瑪昆茨的繪畫作品正是尋找一種普世關聯的嘗試。[6]
2021年,阿爾高藝術館舉辦展覽《艾瑪·昆茨的宇宙:與當代藝術對話的願景》(Kosmos Emma Kunz: A Visionary in Dialogue with Contemporary Art),展出了昆茨60幅作品。次年,即2022年,《艾瑪·昆茨的宇宙:與當代藝術對話的願景》巡展來到西班牙巴斯克自治區的“塔巴卡萊拉(Tabakalera)”文化中心——一個由舊煙草工廠改建而成的藝術空間,其名稱在巴斯克語中正是“煙草工廠”的意思。在這裏,我們注意到觀眾在某種程度上感知到了畫作中藴含的數學,並渴望獲得更深層次的解讀:
對於塔巴卡萊拉的文化總監來説,昆茨作品對於觀眾視線的吸引有雙重效應:“她的創作具有一種獨特的張力:既引人深入細節,探索她精密而細緻的創造,又允許觀者在觀看時保持某種距離——以辨識她所追尋的圖式、秩序、韻律與能量。”[15]
最後,我們要提一下位於瑞士維倫洛斯的“艾瑪·昆茨中心”——這是一個專為昆茨設立的機構,並持續更新展覽。
以上敍述清楚地表明,艾瑪·昆茨的作品如今廣為人知,然而其中藴含的數學卻並非如此。令人驚訝的是,我們文中使用的幾幅圖都有一箇中心焦點(central focal point)。這種焦點強化了圖像的冥想性和輻射性。接下來,我們將從昆茨的通靈藝術轉向其作品背後的數學。我們將探討昆茨的三幅作品,均是由直線族的包絡線構成。
尋找包絡
包絡在數學中頻繁出現。例如,在線性代數中,包絡可以被用於求解和分析一個矩陣的數值域,即包含該矩陣特徵值的集合。(更多的相關內容見 [7]。其他相關的材料亦可見《數學通訊》(The Mathematical Intelligencer)期刊最近的一篇文章[5]。)包絡這一概念也被視為基礎內容,出現在柯朗的微積分教材中 [4, p.171]。正如卡爾曼(Dan Kalman)在《用包絡線方法解梯子問題》[8]一文中寫道:“這給了我們一個藉口來重新討論一個美妙主題:曲線族的包絡。”卡爾曼這篇文章標題中的梯子問題,本質上是探究如何在轉角移動一個梯子(見圖4)。(注6:別把它和“沙發問題”搞混了[12]。)
梯子問題的解恰好就是柯朗書中四個包絡線例子之一。如果這個梯子是單位長度的,則圖像中這些梯子線族的包絡(即與圖4中所有梯子直線相切的曲線)可以表達為
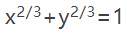 因此這個包絡是星形線的一部分。另外最近一篇清晰明瞭的文獻是格雷戈裏·奎內爾(Gregory Quenell)的文章[11],其中包括對絃線藝術的探討,以及多個包絡線的實例,包括梯子問題——研究等長直線族的包絡線。昆茨的畫作則展現的是另一番藝術景象。
因此這個包絡是星形線的一部分。另外最近一篇清晰明瞭的文獻是格雷戈裏·奎內爾(Gregory Quenell)的文章[11],其中包括對絃線藝術的探討,以及多個包絡線的實例,包括梯子問題——研究等長直線族的包絡線。昆茨的畫作則展現的是另一番藝術景象。
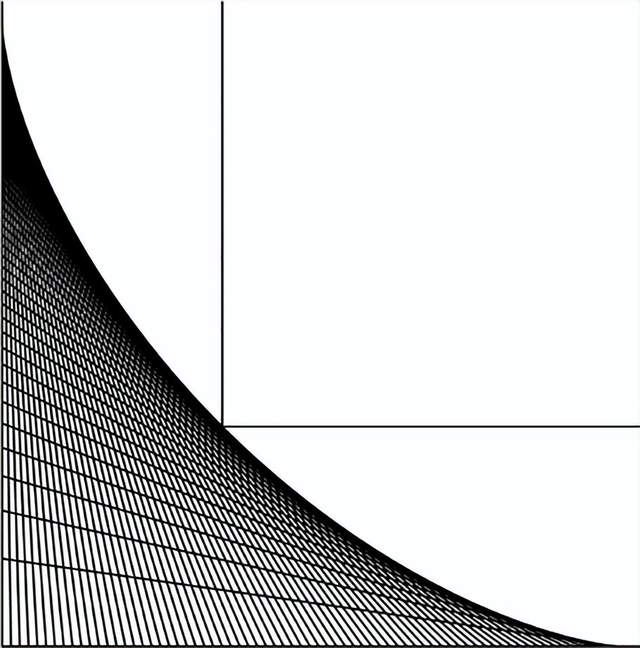 圖4 梯子問題
圖4 梯子問題
數學上關於包絡線的定義有很多種,但我們當前語境下,幾何包絡線的定義或許是最直觀的:
 需要指出的是,包絡線有多種不同的定義方式,其中一些定義所涵蓋的曲線範圍更為寬泛。根據文獻 [2],我們接下來將介紹的包絡線算法,同樣定義了一種意義下的包絡線[4]。柯朗將其稱為“判別曲線”(Discriminant curve),因此我們稱之為“判別包絡線”(Discriminant envelope)。在本文例子中,判別包絡線與幾何包絡線是相同的。我們將在後文圖像中直觀呈現這一點。在正式定義包絡線算法之前,有必要先建立對其推導過程的直觀理解。
需要指出的是,包絡線有多種不同的定義方式,其中一些定義所涵蓋的曲線範圍更為寬泛。根據文獻 [2],我們接下來將介紹的包絡線算法,同樣定義了一種意義下的包絡線[4]。柯朗將其稱為“判別曲線”(Discriminant curve),因此我們稱之為“判別包絡線”(Discriminant envelope)。在本文例子中,判別包絡線與幾何包絡線是相同的。我們將在後文圖像中直觀呈現這一點。在正式定義包絡線算法之前,有必要先建立對其推導過程的直觀理解。
 絡線與該直線族中的每條線在某一點相切。並且這條包絡線上每一點都必須和直線族中某一條線相切。一般來説,一條曲線可以在不同的位置上和不止一條直線相切,但幸運的是,如果合適地限制定義域,並且利用圖形的對稱性,我們可以避免這種情況。因此在一個合適的區間上,我們可以選擇光滑函數F,x,y,使得F(x(t),y(t),t)=0。
絡線與該直線族中的每條線在某一點相切。並且這條包絡線上每一點都必須和直線族中某一條線相切。一般來説,一條曲線可以在不同的位置上和不止一條直線相切,但幸運的是,如果合適地限制定義域,並且利用圖形的對稱性,我們可以避免這種情況。因此在一個合適的區間上,我們可以選擇光滑函數F,x,y,使得F(x(t),y(t),t)=0。
第二個有助於構建包絡線算法的性質可能不是很明顯。以下是一種理解方式:首先,限制

 3. 結合前兩步得出的方程,消去t得到包絡線方程。
3. 結合前兩步得出的方程,消去t得到包絡線方程。
柯朗在[4, p.173]中寫道,“在求得判別曲線之後,仍有必要對每個具體情形進行深入分析,以判斷該曲線是否真正構成包絡線,或在何種程度上偏離包絡線的定義。” 在下文中,我們將構建自己的圖像,並與昆茨的作品進行對比。畢竟,唯有親見,方能相信。
隨處可見的拋物線
藉助包絡線算法,我們可以十分自然地推導出艾瑪·昆茨靈擺幾何繪畫中所藴含的包絡曲線。接下來,我們將具體探討她的三幅作品。
作品No.13
觀察圖5,畫面不僅關於原點對稱,並且關於x軸和y軸對稱。作為一幅視覺作品,色彩為整體構圖注入了石墨線條所無法賦予的生命與活力。然而從數學角度,真正令人着迷的,正是那些石墨線條。
 圖5 昆茨的013號作品(圖片由艾瑪·昆茨基金會提供)
圖5 昆茨的013號作品(圖片由艾瑪·昆茨基金會提供)
從圖5可以觀察到,石墨線條衍生出四條跨越不同象限、彼此相似的曲線。通過包絡線算法,我們可以為每一條邊界曲線推導出閉合表達式。仔細觀察便會發現,昆茨並沒有畫完所有的線條——如果我們想象這幅作品代表一隻眼睛,似乎在她勾勒出虹膜完整的周邊區域時便戛然而止了(注7:我們將其視為眼睛這一解讀得益於艾瑪·昆茨中心的卡琳·凱吉(Karin Kägi)的提示)。因此,我們得到的曲線是下文所討論曲線的子集。我們將闡述如何推導這些包絡線的方程,並且概述應用包絡線算法的一般過程。
首先,我們必須考慮關於繪畫的一些假設。我們使用了博物館提供的一件複製品,其中每條線均按照方格紙上間隔約兩格(總計1釐米間距)沿着橫縱軸線繪製而成。繪圖本身被設定在一個邊長為40個單位的正方形區域,並以座標原點為中心。當然,昆茨繪製的線條數量有限,但這些線條卻形成了看似連續光滑的曲線。為了應用包絡線算法,我們讓t在整個區間內取值。
 在這幅作品中存在多組曲線,還有很多直線從中心向邊界放射延伸,而這些直線僅相交於原點,所以根據前面包絡線定義,該直線族不存在包絡線。此外,在每個角還有對角線族,其連線勾勒出跨越圖畫中不同角落的弧形。這些直線族將成為包絡線算法的研究對象,我們希望能夠求出其數學表達式。
在這幅作品中存在多組曲線,還有很多直線從中心向邊界放射延伸,而這些直線僅相交於原點,所以根據前面包絡線定義,該直線族不存在包絡線。此外,在每個角還有對角線族,其連線勾勒出跨越圖畫中不同角落的弧形。這些直線族將成為包絡線算法的研究對象,我們希望能夠求出其數學表達式。
先考慮主要位於第一象限的直線族,我們觀察到該族包含40條直線。這些直線的斜率逐漸變化,從水平線y=20到垂直線x=20。(假設原點位於中心,繪圖的寬度為[-20,20])該直線族一種可能的參數化可以定義為以下方程的(x,y)解集,
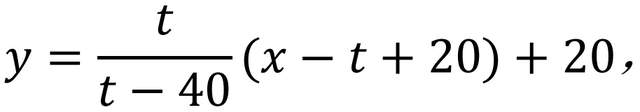



 圖6 線族疊畫在第一象限
圖6 線族疊畫在第一象限
作品NO.009
圖7展示了編號009的作品,其尺寸為101釐米×101釐米。在這幅作品中,我們採用與之前文類似的包絡線算法,可以得到空白區域八條邊界曲線的封閉形式解。接下來,我們將詳細描述其中一條曲線。
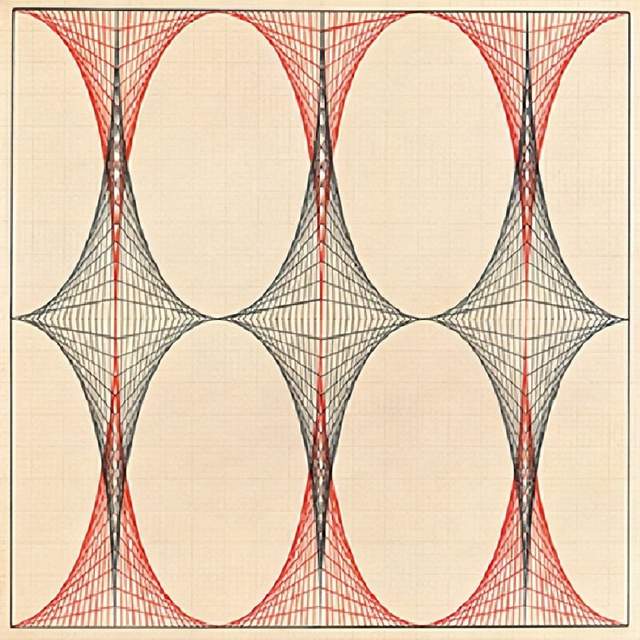 圖7 昆茨的009號作品(圖片由艾瑪·昆茨基金會提供)
圖7 昆茨的009號作品(圖片由艾瑪·昆茨基金會提供)
在No.009號作品中,我們觀察到存在八個矩形區域,其中在頂部和底部的第一個和最後一個矩形互為鏡像對稱,而中間的兩個區塊則包含着空白區域,其邊界為簡單的閉合橢圓形曲線。我們先考慮該橢圓形狀四分之一的部分,其餘部分可通過昆茨反覆運用的對稱變換生成。與之前類似的是,紅藍直線與矩形邊界的交點大致是等距分佈,但縱軸方向的間距是橫軸間距的三倍。
探究圖7與圖5相似性的關鍵在於x軸與y軸對應數值是等距分佈這一條件。我們稍後會解釋這一點,但很明顯的是,包絡線算法與之前一樣有效:儘管我們當前所參考的圖像略顯模糊,但經估算,每一半矩形的寬度約為 16 個單位,長度約為 48 個單位。
在算法中,我們放置原點使得矩形區域邊界點為(-16,0),(16,0),(16,48),(-16,48)。由於我們只是縮放x軸和y軸,所以我們猜測包絡線仍是一段拋物線弧,而事實正是如此!因此,儘管昆茨這兩幅作品視覺上存在差異,但No.009作品(圖7)其實包含了我們在她No.013作品中曾看到過的圓錐曲線的縮放與重複的版本。
假設這些垂直線之間的間距均勻,且每次間隔三個單位,那麼其中一族直線(對應於圖形右上角)可以由下列公式給出,
-t(y-48)=(48-3t)(x-16+t)
其中,參數t∈[0,16]。(譯者注:這裏直線族構造是類似的,考慮直線y=48與直線x=16上,並且在繪圖寬度內平均分佈的離散點,座標為(16-t,48), (16,3t),便可求得直線族的參數化。)
在這種情況下,我們可以得到,
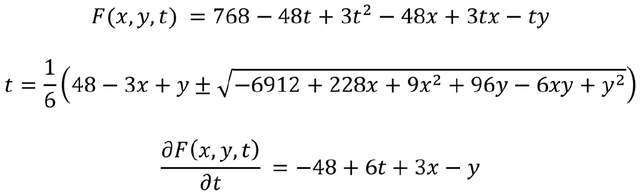
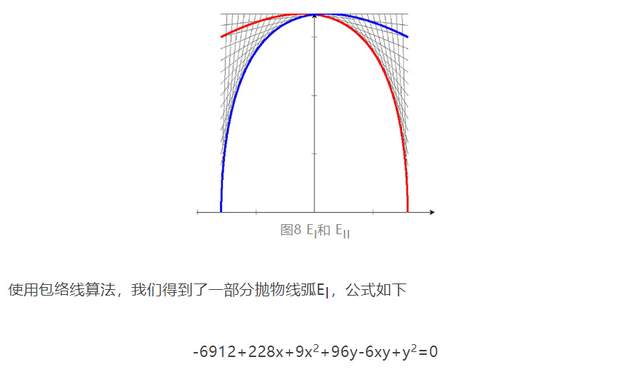 將該曲線與艾瑪·昆茨繪製的直線族對比,我們可以從圖8中觀察到,紅色拋物線EI在第一象限確實形成了包絡線結構。圖中藍色拋物線EII亦可通過相同方法推導出,其對應的直線族可以沿用之前的參數化方法。特別之處在於,這一看似橢圓的形狀實際上並非真正的橢圓,這些閉合曲線由四條不同的拋物線弧段拼接而成。
將該曲線與艾瑪·昆茨繪製的直線族對比,我們可以從圖8中觀察到,紅色拋物線EI在第一象限確實形成了包絡線結構。圖中藍色拋物線EII亦可通過相同方法推導出,其對應的直線族可以沿用之前的參數化方法。特別之處在於,這一看似橢圓的形狀實際上並非真正的橢圓,這些閉合曲線由四條不同的拋物線弧段拼接而成。
作品No.130
分析圖9可以看出,其x軸均勻的間距與直線上y=x上均勻間距不同,但圖中依然包含拋物線弧。我們依據算法推導出直線方程,
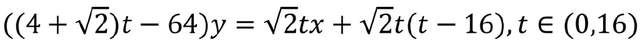 以及第一象限中在x>y條件下拋物線的方程
以及第一象限中在x>y條件下拋物線的方程