龐加萊的博士論文寫完，就立成經典_風聞

譯者按

伯克霍夫是微分方程、動力系統和混沌理論等領域的大家，在其中多有建樹，同時也繼承並發展了龐加萊在此的諸多研究工作。本文是伯克霍夫對《龐加萊文集》第一卷的書評。在此文中，作者較為系統和具體地總結龐加萊的微分方程及相關研究；同時，此文還涉及龐加萊的微分方程研究與他的拓撲和自守函數研究的相互關係。這對我們理解和探究龐加萊及其數學創造活動整體有重要意義。

撰文 | 伯克霍夫（G. D. Birkhoff）

翻譯 | 金威

本書是《亨利·龐加萊文集》（The Collected Works of Henri Poincaré；以下簡稱《文集》）出版的第二本，文集中最先出版的是1916年出版的第二卷[1]。該卷收錄了他在一般自守函數領域的貢獻，而本卷則主要收錄他關於常微分方程、偏微分方程和線性差分方程的研究工作。《文集》的編輯順序與龐加萊自己的論文集的《分析》（Analyse）部分[2]所載的順序一致。前兩卷中有關《分析》的內容已經在第一卷開始時提及，這對讀者很有幫助。後續卷冊也將沿用類似的編排計劃。

龐加萊非凡數學工作的起點是他於1878年在《綜合理工學院學報》（Journal de l’École Polytechnique）上發表的《關於微分方程定義的函數性質的註記》（Note sur les propriétés des fonctions définies par les équations différentielles）。一個如下的一階常微分方程系統：

龐加萊便着手將這個線性偏微分方程作為理論基礎，研究系統 (1) 在此類奇點附近的解。

龐加萊在 1879 年完成的博士論文《關於由偏微分方程定義的函數的性質》（Sur les propriétés des fonctions définies par les équations aux différences partielles）中闡

如果這些限制條件未被全部滿足，則只能得到部分結果。事實上，在所有λi都相等的特殊情況下，龐加萊的方法就完全失效了。然而，龐加萊成功地探索了其中各種有啓發性的典型例子。對於其一般情況，儘管已取得了很大進展，但迄今為止仍缺乏系統的處理方法。

隨着對系統 (1) 的局部解的研究如此成功地開始，龐加萊自然而然地將他的研究成果應用於對大範圍內實數解的研究，特別是在最簡單的n=2的情況下，此時式 (1) 可以寫為

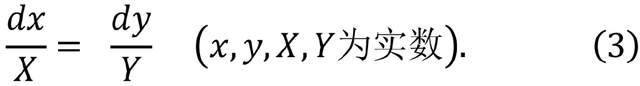他的偉大論文（memoir）《關於由微分方程定義的曲線》（Sur les courbes définies par des équations différentielles）分四部分發表在《純粹與應用數學雜誌》（Journal de Mathématiques Pures et Appliquées，1881-1886年）[3]上，其中前三部分以精湛的方式論述了這類方程。本論文的第四部分涉及n=3的類似問題。我們可以參考阿達馬（Hadamard）在1925年剛剛出版的《萊斯研究所講座》（Rice Institute Lectures）[4]中對這一工作的分析，讀者還可以在其中找到有關這一領域後續發展的參考文獻。在龐加萊對n=2的情況的處理中，最基本的是將(x,y)幾何地表示為平面或曲面上的一個點，而方程(3)則

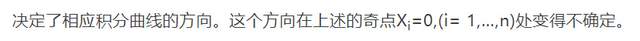龐加萊這篇論文的前三部分可視為最簡單的實微分方程系統（即一階的單個方程）理論的基礎。事實上，它們可能永遠是這一領域最重要的著作。拉格朗日（Lagrange）、雅可比（Jacobi）和其他數學家將注意力集中在可積情況上，或者至少滿足於通過已知的積分儘可能地降低階數。在天體力學領域，拉普拉斯（Laplace）和後來的理論天文學家一直滿足於使用形式級數作為系統計算的手段。但是，龐加萊是第一個從純粹數學的角度來探討不可積的微分方程系統的一般問題的人。他在這一研究方向上對n=2的主要研究成果載於上述論文中。他後來在天體力學方面的大部分工作可被視為與n>2的特殊重要情況有關，特別是n減為3時的三體問題。

即使在n=2的情況下，有趣的“位置分析學”（analysis situs）問題[5]也呈現在龐加萊面前。一個重要的問題是[6]：假設給定一個一對一的直接連續變換（direct continuous

解析時，龐加萊也未能證明上述粗體字部分的假設成立；儘管只要f(θ)是連續的，他就能證明該假設無需滿足。當茹瓦（Denjoy）在1932年出色地解決了這個非常困難而又有趣的開放問題[7]，他證明如果f(θ)是連續的，並且全變差（total variation）有限[8]，那麼該假設就會自動成立。

正是由於龐加萊試圖處理n>3的情況，他才開始了後來的位置分析學研究，因為他自己在《分析》中寫道：“為了更進一步，我必須創造一種幾何工具，而當我希望深入到三維以上的空間時，卻缺乏這種工具。我這是促使我開始研究位置分析學的主要原因。”此外，關於當茹瓦解決的上述具體問題，龐加萊實際上表明，他的一些結果與天體力學中已知事實之間的類比，無疑會使他以後再回到這個問題上來。因此，他在這篇論文中的研究直接導致了他後來在位置分析學和天體力學領域的基礎性工作。

龐加萊幾乎是同時開始研究上述n=2,3兩種情況下的非線性常微分方程，以及n階線性常微分方程和差分方程的。事實上，雖然他關於線性微分方程和差分方程的第一篇論文發表在1883年的《美國數學雜誌》（American Journal of Mathematics）上，但正如他自己所説，大部分結果已經包含在他1880年未獲獎的論文中。富克斯（Fuchs）和其他人關於線性常微分方程的研究主要侷限於正則奇點的情況——一種非常特殊的情況，而龐加萊則很好地處理了非正則奇點。在這方面，有必要提及物理學家斯托克斯（G. G. Stokes）在更早時（1857年）發表的一篇非常有啓發性的論文，題目為“關於出現在發散延拓中的任意常數的不連續性” (On the discontinuity of arbitrary constants which appear in divergent developments）[9]。斯托克斯在文中詳細研究了貝塞爾方程在整個複平面內的解的行為；該方程在無窮遠處有一個非正則奇點。龐加萊似乎並不知道這篇極具啓發性的論文，因為他沒有在任何地方提到過它。

龐加萊在這一領域的主要進展是證明了在特定條件下，託梅（Thomé）和法布里（Fabry）的已知形式級數解代表了複平面的適當部分（sector）處線性微分方程的實際解，與斯特林公式作為函數 Γ(n)的漸近表示的意義相同。他在線性差分方程中發現了一個類似的結果。龐加萊在這一領域的論文為給出此類線性方程的一般理論做出了巨大貢獻。然而，直到最近，這種方程的一般理論才得以發展。[10]

本卷的最後一篇論文是上文提到的那篇不太令人滿意的未獲獎論文的第二部分，直至1923年才在《數學學報》上發表。在這裏，我們發現了對以下問題的初步處理：對一個具有多項式

線性獨立解，則x是z的亞純函數。這個問題由富克斯在1880年提出並部分解決，而龐加萊的文章主要是對富克斯工作的評論（critique）。在這篇文章中，我們可以找到龐加萊在自守函數理論方面的研究成果，它收錄在《文集》第二卷中。

第一卷的讀者也將非常感謝德拉奇（Drach）教授所做的認真且非常稱職的修訂。

參考文獻及註釋

[1] 我也評論了該卷；見Bull. Amer. Math. Soc., Volume 40, Number 5 (1934), 363-366. 譯者注：中譯見返樸文章《伯克霍夫：龐加萊在自守函數領域的研究》。

[2] 譯者注：Analyse 位於龐加萊文集的卷首。在此部分中，龐加萊扼要地將自己的文集分為七個領域：1. 微分方程；2. 函數的一般理論；3. 純數學雜項（代數、算術、羣論、位置分析）；4. 天體力學；5. 數學物理學；6. 科學哲學；7. 教學、普及、雜項（參考文獻、各類報告）。

[3] 譯者注：Journal de Mathématiques Pures et Appliquées 是世界上第二古老、且仍持續出版的數學期刊。它由法國數學家約瑟夫·劉維爾（Joseph Liouville，1809-1882）創立，自 1836 年起在巴黎出版，其影響力極大地刺激了 19 世紀法國數學的氣氛。因此在此處該雜誌被稱為“劉維爾的雜誌”（Liouville’s Journal），以表示對他的紀念。

[4] The later scientific work of Henri Poincaré, Rice Institute Pamphlets,vol. 20 (1933).

[5] 譯者注：即“拓撲學”的原名。

[6] 見其論文第三部分第15 章

[7] Sur les caractéristiques à la surface du tore, Comptes Rendus, vol. 194 (1932)

[8] 譯者注：即f為有界變差函數。

[9] Transactions of the Cambridge Philosophical Society, vol. 10.

[10] 可參見我與 Trjitzinsky 合著的文章, Analytic theory of linear difference equations, Acta Mathematica, vol. 60 (1932), 和另一篇 Trjitzinsky 的文章：Analytic theory of linear，在同刊的vol. 62。

本文譯自G. D. Birkhoff, The Work of Poincaré on Differential Equations, Bull. Amer. Math. Soc. 40(5): 363-366 (May 1934).

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。

版權説明：歡迎個人轉發，任何形式的媒體或機構未經授權，不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。